Constrained principal component analysis reveals functionally connected load‐dependent networks involved in multiple stages of working memory

Abstract

Constrained principal component analysis (CPCA) with a finite impulse response (FIR) basis set was used to reveal functionally connected networks and their temporal progression over a multistage verbal working memory trial in which memory load was varied. Four components were extracted, and all showed statistically significant sensitivity to the memory load manipulation. Additionally, two of the four components sustained this peak activity, both for approximately 3 s (Components 1 and 4). The functional networks that showed sustained activity were characterized by increased activations in the dorsal anterior cingulate cortex, right dorsolateral prefrontal cortex, and left supramarginal gyrus, and decreased activations in the primary auditory cortex and “default network” regions. The functional networks that did not show sustained activity were instead dominated by increased activation in occipital cortex, dorsal anterior cingulate cortex, sensori‐motor cortical regions, and superior parietal cortex. The response shapes suggest that although all four components appear to be invoked at encoding, the two sustained‐peak components are likely to be additionally involved in the delay period. Our investigation provides a unique view of the contributions made by a network of brain regions over the course of a multiple‐stage working memory trial. Hum Brain Mapp, 2011. © 2010 Wiley‐Liss, Inc.

INTRODUCTION

Working memory can be described as the ability to hold a limited amount of information in an active state, for use in guiding behavior after the information is removed from the environment [Baddeley and Hitch, 1974]. A common approach to testing working memory experimentally using functional magnetic resonance imaging (fMRI) involves the delayed recognition task. Experiments using delayed recognition involve three stages: (1) encoding, during which items to remember are presented, (2) delay, during which the previously presented items must be maintained, and (3) probe, during which a recognition test for the previous items is administered. Functional neuroimaging investigations often attempt to identify and localize cognitive processes engaged by these individual task stages.

However, one limitation of many such investigations is that the stages are assessed separately and in isolation to one another. As a result, there is limited knowledge on how the involved brain regions change over the course of a delayed recognition trial, making inferences on the extent to which distinct networks of regions contribute separately to each task stage difficult [Postle, 2006]. In addition, as has been previously noted [e.g., Cairo et al., 2004; Manoach et al., 2003; Woodward et al., 2006), attempts to analyze fMRI data by modeling stage‐specific working memory processes can lead to a number of methodological concerns, particularly when stage‐specific hemodynamic response functions (HRFs) are used in prediction models. Because of the assertion of an assumed HRF shape associated with each specific task stage, the estimated blood oxygen level‐dependent (BOLD) response for any given stage is, by virtue of the application of multiple regression, restricted to a scaled version of the model's shape. Because there is substantial overlap between the HRF modeled for each task stage, and because these stages necessarily occur in a fixed order, any mismatches between the model and the “true” evoked BOLD signal shape for that stage is likely to result in an automatic, statistically induced misattribution of signal to the incorrect task stage. For example, any encoding‐specific BOLD signal that is not fit well by the encoding‐labeled HRF model (e.g., more prolonged than expected) may be fit by the delay‐labeled model and would therefore be automatically misattributed to the delay stage by the statistical procedure [see Manoach et al., 2003, for a simulation of this misattribution risk]. Moreover, highly correlated predictors in multiple regression are associated with inflated standard errors [Pedhazur, 1982, p 245], resulting in unstable parameter estimates. Although important advances have been made regarding how some of these problems can be avoided by adjusting the timing of the experimental design [Ollinger et al., 2001] and the placement of impulse response functions in the model [Zarahn et al., 1997], in addition to sometimes requiring potentially undesirable changes to the behavioral task paradigm, this area of research is still susceptible to interpretative errors caused by labeling potentially inaccurate hemodynamic response models of task stages. This is a particularly pertinent point for delayed recognition tasks, for which an assumed shape of evoked responses is important for interpreting whether or not a region is involved in a particular task stage [e.g., sustained delay period activity reflecting storage‐ and maintenance‐related processes; Postle et al., 2000].

Data analytic approaches that focus on peristimulus time (i.e., on the time points immediately following, or preceding and following, presentation of the imperative stimulus) instead of isolated task stages avoid the interpretational errors associated with automatic misattribution of signal to the incorrect task stage. Using a deconvolution approach focusing on peristimulus time, minimal assumptions are made regarding the shape of evoked responses of interest [Dale and Buckner, 1997; Glover, 1999]. Thus, unlike modeling task stages with synthetic HRF models, this method does not impose the assumption that the brain processes involved in working memory are organized according to the discrete stages of the behavioral task. One of the simplest and least constrained approaches to deconvolution is the finite impulse response (FIR) approach, which provides an estimate of average BOLD response amplitude for a number of peristimulus time points [Henson et al., 2001; Serences, 2004]. A univariate FIR model approach has previously been employed in a working memory study [Manoach et al., 2003], but such an analysis produces images of neural activation computed separately for each peristimulus time point, and so difficulties arise in formally selecting the “correct” time points for further inspection, and as a result, also in determining the progression of activation change over peristimulus time points.

In contrast to univariate methods, multivariate analyses methods using a FIR model can extract patterns of intercorrelation among voxels that are determined by, and can be mapped back to, coordinated changes in BOLD signal over peristimulus time, thereby allowing estimated changes in activation in a single neural network to be followed over peristimulus time. Several methods exist which permit this, but if functional connectivity is to be approached in a whole‐brain exploratory fashion, whereby any voxel could potentially load onto the network, then methods which involve a priori specification of specific regions of interest, such as dynamic causal modeling or structural equation modeling [Penny et al., 2004], are not suitable. A number of exploratory multivariate methods are available. Some, such as principal component analysis [Viviani et al., 2005] and independent component analysis [ICA; McKeown et al., 1998] do not take into account information about the stimulus timing before computing the neural networks (it should be noted that ICA methods are now being developed that allow this; [Calhoun et al., 2005]). Other exploratory methods incorporate information about stimulus timing into the computations before extracting patterns of intercorrelation and focus on summarizing the patterns of inter‐relationship between two sets of variables (the obtained BOLD data and the model). Examples of these model‐based methods are partial least squares [PLS; McIntosh et al., 2004], canonical variates analysis [CVA; Strother et al., 2004], and multivariate linear models method [MLM; Worsley et al., 1997]. In the current study, we use an approach that falls into this model‐based category referred to as FIR‐based constrained principal component analysis (FIR‐CPCA; http://www.nitrc.org/projects/fmricpca). More detail about how FIR‐CPCA compares with other methods that decompose inter‐relationships between two sets of variables will be presented in the Discussion section.

In the current study, we employed FIR‐CPCA to visualize, across multiple subjects, how functional networks change over the course of a multistage behavioral trial (i.e., over peristimulus time) and how these networks respond to experimental manipulations. Using a variable memory load delayed‐recognition data set, we demonstrate how this approach allows (1) the determination of multiple functional networks involved in working memory, (2) the estimation of the pattern of BOLD changes associated with each functional network over the course of a trial, (3) a statistical test of the reliability of the HRF associated with each component, and (4) a statistical test of the degree to which experimental manipulations (in this case working memory load) affect each functional network.

METHODS

Details regarding the motivation for task design, nature of the sample, and data acquisition have been published previously [Cairo et al., 2004]; a summary is presented here. Subjects were 18 right‐handed, healthy, native English speakers (10 women, mean age 27.50 years, age range 18–35). Written informed consent was obtained before participation, and all experimental procedures were approved by the University of British Columbia's Clinical Research Ethics Board. Subjects performed a variable load delayed recognition working memory task while undergoing fMRI. During a single trial of this task, subjects viewed a string of 2, 4, 6, or 8 differing uppercase consonants for 4 s, which they were instructed to remember over a short delay. Following the delay, a single lowercase consonant was shown for 1 s. Subjects were asked to decide whether this letter had been included in the preceding letter string. Binary responses were indicated by right‐handed index and middle finger presses, and the finger‐response assignments were counterbalanced across subjects. The probe stage was followed by an intertrial interval of 3, 4, or 5 s in duration. Twenty percent of the experimental trials were followed by a blank trial of similar length in which the world “Relax” was projected on the screen. The jittering of the delay phase and the intertrial interval, and the blank trials, were implemented in order to optimize the experimental design according to available recommendations [Dale, 1999].

Echo‐planar images were collected on a standard clinical GE 1.5 T system fitted with a Horizon Echo‐speed upgrade. Conventional spin‐echo T1 weighted sagittal localizers were used to view the positioning of the participant's head and to graphically prescribe the functional image volumes. Functional image volumes were collected with a gradient echo (GRE) sequence (TR/TE 3,000/40 ms, 90 flip angle, FOV 24 × 24 cm², 64 × 64 matrix, 62.5 kHz bandwidth, 3.75 × 3.75 mm² in plane resolution, 5.00 mm slice thickness, 29 slices, 145 mm axial brain coverage). Each stimulus run consisted of 194 scans (encompassing the entire brain). The first 12 s (4 scans) collected at the beginning of each run were discarded, to avoid variation due to T1 saturation effects. Functional images were reconstructed offline. Statistical parametric mapping software (SPM2, Wellcome Institute of Cognitive Neurology, London, UK, http://www.fil.ion.ucl.ac.uk/spm) was used for image realignment and normalization into Montreal Neurological Institute (MNI) anatomical space (resampled to 4 × 4 × 4 mm³ voxel sizes), and spatially smoothed using a Gaussian kernel (8 mm FWHM).

Constrained Principal Component Analysis

Most fMRI experiments are designed to determine how stimulus presentations cause BOLD signal to change; therefore, from this perspective, information about the stimulus presentations should be considered a set of predictor variables, and the BOLD signal a set of criterion variables. A multivariate analysis method that takes this conceptual framework into consideration is CPCA [Takane and Shibayama, 1991]. CPCA is a general method for structural analysis of multivariate data that combines regression analysis and principal component analysis into a unified framework. As for typical principal component analysis on fMRI data, this method derives images of functional neural networks from singular‐value decomposition of BOLD signal time series; however, CPCA allows derivation of images when the analyzed BOLD signal is constrained to that aspect of variance in BOLD signal that is predictable from how the stimuli were presented.

We now briefly present the matrix equations for the current application of CPCA [for the comprehensive CPCA theory and proofs please see Hunter and Takane, 2002; Takane and Hunter, 2001; Takane and Shibayama, 1991]. This involves preparation of two matrices. The first matrix, Z, contains columns of normalized and smoothed subject‐mean‐centered activations for all voxels over all scans. The second matrix, G, can be referred to as the design matrix. It contains models of the expected BOLD response to the timing of stimulus presentations. The matrix of BOLD time series (Z) and design matrix (G) are taken as input, with BOLD in Z being predicted from the model in G. To achieve this, multivariate least‐squares linear regression is carried out, whereby the BOLD time series (Z) is regressed onto the design matrix (G):

(1)

where C = (G′G)⁻¹ G′Z. This analysis yields condition‐specific regression weights in the C matrix (i.e., regression weights specific to the experimental conditions as defined by the design matrix). The condition‐specific regression weights are often referred to (in conventional fMRI analyses) as beta images. GC contains variability in Z that is predictable from the design matrix G, that is to say, variability in Z that is predictable from a model of BOLD response to the timing of stimulus presentation.

The next step involves extracting a component (or components) that represents a network (or networks) of functionally interconnected voxel activations that are related to the experimental stimulus presentations. This involves singular value decomposition of the activation variability that was predictable from the design matrix (GC). The maximum number of extractable components is equal to the rank of GC, which is the minimum row or column subscript of G:

(2)

where U = matrix of left singular vectors; D = diagonal matrix of singular values; and V = matrix of right singular vectors. Each column of V can be overlaid on a structural brain image to allow visualization of the neural regions involved in each functional network. In the current application of CPCA, we orthogonally rotated and rescaled (by D) the V matrix before display, so that a rotated loading matrix (VD) is displayed. The values of the loading matrix are weights that represent the contribution of each component (functional network) to the variance of each column of GC and can be scaled to contain the correlations between the components in U and the variables in GC.

To interpret the components with respect to the conditions represented in G, we produced predictor weights [Hunter and Takane, 2002] in matrix P. These are the weights that would be applied to G to create U (U = G×P). They indicate the importance of each column in the G matrix to the network(s) represented by the component(s), so are essential for relating the resultant components to the experimental conditions of interest represented in G.

Preparation of Z and G

To prepare the Z matrix for the current data, SPM2 was first used to realign, spatially normalize and smooth BOLD data. A binary brain mask image obtained from a random‐effects SPM2 analysis was used to extract the BOLD signals in 23,929 voxels from each of 190 scans data collected from each individual subject. This produced a matrix of BOLD signals consisting of 3,420 rows (18 subjects ×190 scans) and 23,929 columns. Then the matrix Z was standardized to have zero mean and unit standard deviation in each column for each subject.

In the analysis reported here, the G (design) matrix consisted of a FIR basis set, as opposed to the HRF model employed in past studies [Cairo et al., 2004, 2006; Woodward et al., 2006]. The FIR model estimates the change in BOLD signal at specific peristimulus scans relative to all other scans. The value 1 is placed in rows of G for which BOLD signal amplitude is to be estimated, and the value 0 in all other rows (resulting in “mini boxcar” functions). The time points coded by this model were the 1st to 8th repetition times (TR) following stimulus presentation. As the TR for these data was 3 s, this resulted in estimating BOLD signal over a 24 s window, with the start of the first time point (time = 0) corresponding to encoding stimulus onset. Thus, the encoding, delay, and probe stages were not modeled separately; rather, all stages are covered by this 24 s window of peristimulus time. The columns in this subject‐and‐condition based G matrix code 8 peristimulus time points for each of four load conditions (2, 4, 6, and 8 letters), for each subject, totaling 576 columns (8 × 4 × 18 = 576). The matrix equations for FIR‐CPCA using the matrix dimensions for the current study (and extracting four components as in the present study) would then be:

(3)

(4)

The columns of G represent points in peristimulus time for each condition and subject combination; therefore, the predictor weights in ₅₇₆ P ₄ (_3,420 U ₄ = _3,420 G ₅₇₆ P ₄) are the values that determine the contribution of each peristimulus time point, for each condition and subject, on the temporal variation in the functional networks over scans. These predictor weights are therefore appropriate for use in familiar tests of statistical significance, such as analysis of variance (ANOVA; see below).

As the sign of a singular vector is arbitrary, positive values in the loading matrix (VD) do not necessarily imply activation increases. Therefore, in order to ensure correspondence between the interpreted directionality of the hemodynamic response represented by the predictor weights and activation increases/decreases, for each component, the trial‐averaged BOLD signal contained in Z was extracted for the voxels showing the most extreme 5% of component loadings, and this was displayed separately for positive and negative component loadings.

Statistical Test of Load Dependence

For each component, predictor weights were produced for each combination of peristimulus scan, load condition, and subject. These weights can be used to statistically test the effect of peristimulus time, to determine whether or not the values in the P matrix are reflecting a hemodynamic response and not varying randomly around zero. The effect of increasing memory load can also be tested, as can the interaction between peristimulus time and load. Leaving out the first point of peristimulus time (which was adjusted to zero for predictor weights in all conditions for the purposes of display and data analysis), this analysis would be carried out as a 7 × 4 within‐subjects ANOVA for each component, with the factors of time point (time points 2–8 after the initiation of a task trial) and Load (2, 4, 6, and 8 letters) as the within‐subject factors. Tests of sphericity were carried out for all ANOVAs. Greenhouse‐Geisser adjusted degrees of freedom are reported when violations of sphericity affected interpretation of results; otherwise, the original degrees of freedom are reported.

Component Rotation

Component rotations provide interpretational frameworks with which to understand the data configuration. Infinite rotations are possible, and rotation choice is up to the discretion of the investigator. Any of the three (optionally rescaled) matrices that result from this application of CPCA can be rotated (i.e., VD, U, or P); however, the transformation matrix that is used for the rotation of either VD, U, or P must also be applied to the other two matrices to ensure that all three matrices are aligned to the same orientation. In our previous work [Woodward et al., 2006], we employed promax rotation to VD, and subsequently applied the same transformation to U and P. Promax rotation is based on methods such as varimax and quartimax which are oriented toward finding simple structure [Harman, 1967, p 304; Yates, 1987, p 32], and therefore utilizes the criterion of maximizing the (row‐wise or column‐wise) variance of the squared loadings (i.e., voxel‐based component loadings, or VD). However, with the current FIR‐based application of fMRI‐CPCA, our interpretation of components (with respect to the conditions represented in G) is based not on the voxel‐based matrix VD but on the hemodynamic response shape of the predictor weights contained in P; therefore, it was logical to apply rotation to P for computation of a transformation matrix, and then apply this transformation matrix to VD and U.

The simple‐structure criteria that are traditionally used on VD would not be appropriate for application to P because P is hypothesized to reflect an HRF shape, not polarization of zero and nonzero values. One strategy for rotation of P is to use a Procrustes‐style rotation of P to a target matrix (of the same dimensionality) that represents the HRF shape expected from the experimental design. This would allow the components to reflect an HRF shape, where one is present in the predictor weights, without limiting the predictable variance to specific shapes (and the task stage labels associated with them). However, this method does not allow multiple components to be oriented to various manifestations of the same basic HRF shape because the computation requires the target matrix in a Procrustes rotation be of full rank, disallowing repeated shapes in the target matrix. Our rotation approach involved iteratively generating random Gram‐Schmidt orthogonalized transformation matrices (T), applying them to P, and selecting the PT matrix that most closely matched any of a set of HRF shapes expected to result from the experimental design. The T matrix that resulted from this iterative method was then applied to the other matrices as follows: UT = GPT; VDT; in order to align them to the same orientation as PT. These matrix equations with row and column subscripts matching the current analysis are:

(5)

(6)

(7)

where P* = rotated P matrix; U* = rotated U matrix; and (VD)* = rotated VD matrix.

The steps for optimizing T for rotation of P are detailed below:

• 1Candidate HRF shapes are repeated for all subjects and all conditions, and as such, populate vectors having the same number of rows as P.
• 2A transformation matrix T is randomly generated and Gram‐Schmidt orthogonalized, and P* is computed.
• 3The absolute value of Pearson's correlation coefficient is computed between each column of P* and each candidate HRF shape vector.
• 4The product of the maximum values derived for each column of P* is computed.
• 5Steps 2–4 are iteratively repeated, with the transformation matrix T that maximizes the product computed at step 4 retained as the optimal solution.

In the current study, we used 500,000 iterations with a set of six candidate HRF shapes. To produce the six HRF shapes, we used SPM2 to produce single‐trial time series based on specific task stages predicted by a canonical HRF, convolved with a delta function. Single and combined event models were developed for: (1) encoding only; (2) encoding + delay; (3) delay period only; (4) delay + probe; (5) probe only, and (6) encoding + delay + probe.

RESULTS

Four components were extracted in order to optimize comparison with our previous analysis of the same data [Woodward et al., 2006]. The percentage of variance in GC that was accounted for by Components 1, 2, 3, and 4 in the unrotated solution was 32.63, 4.71, 2.31, and 1.98, respectively. The sum of the squared loadings divided by the number of scans for the rotated solution was 20.48, 9.47, 9.01, and 2.66 for Components 1, 2, 3, and 4, respectively. The neural regions comprising the functional networks represented by each component for FIR‐CPCA and their associated Brodmann's Areas (BAs) are displayed in Figures 1A–4A, with corresponding anatomical descriptions in Tables I–IV. The mean predictor weights were plotted as a function of peristimulus time (see Figs. 1B–4B) and represent the response of each functional network to the delayed recognition task at different memory loads.

Figure 1.

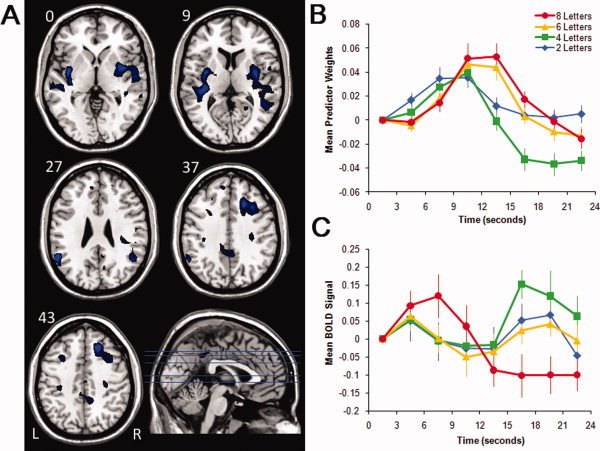
Images, plots of predictor weights, and plots of BOLD signal for Component 1. The dominant 5% of component loadings are displayed (A), with negative component loadings displayed in black (max = −0.32) and blue (min = −0.39). (No positive component loadings passed this threshold.) The mean FIR‐based predictor weights are plotted as a function of peristimulus time in the right panel, top (B; error bars are standard errors). The predictor weights at the first point of peristimulus time are adjusted to zero, and all other values scaled accordingly for each subject, and therefore differ from % signal change by a constant term only. The mean BOLD signal extracted from the regions displayed in (A) are plotted as a function of peristimulus time in the right panel, bottom (C; error bars are standard errors). Axial slices are located at the following Talairach z axis coordinates: 0, 9, 27, 37, 43. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 4.

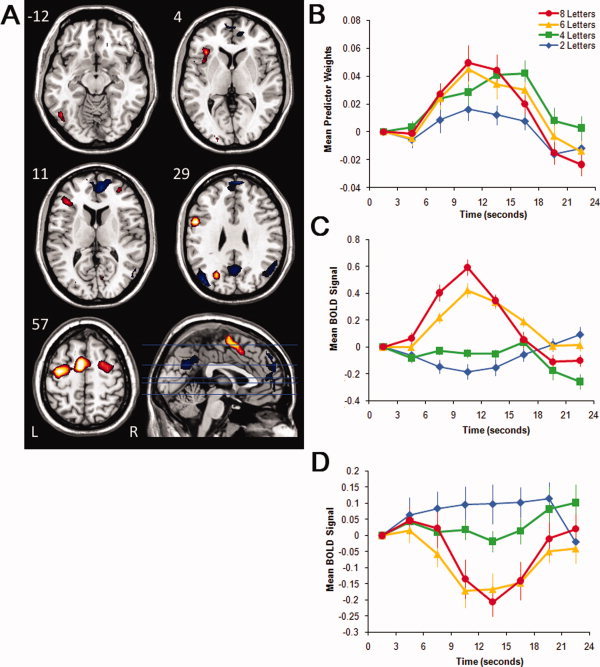
Images, plots of predictor weights, and plots of BOLD signal for Component 4. The dominant 5% of component loadings are displayed (A), with positive component loadings displayed in red (min = 0.17) and yellow (max = 0.29), and negative component loadings are displayed in black (max = −0.17) and blue (min = −0.30). The predictor weights at the first point of peristimulus time are adjusted to zero, and all other values scaled accordingly, and therefore differ from % signal change by a constant term only. The mean FIR‐based predictor weights are plotted as a function of peristimulus time in the right panel, top (B). The mean BOLD signal extracted from the regions comprising the FIR component positive component loadings are plotted in the right panel, bottom (C), and the negative component loadings are plotted in the bottom panel (D; error bars are standard errors). Axial slices are located at the following Talairach z axis coordinates: −12, 4, 11, 29, 57. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table I.

Anatomical descriptions for each cluster (>5 voxels) of Component 1, with corresponding Brodmann's Areas and peak Talairach (XYZ) coordinates

Cortical region	Brodmann's area	Max Talairach coordinate
Cluster 1: Right hemisphere
Superior temporal gyrus	22	51, −8, −10
Insula		36, 0, 4
Middle temporal gyrus	21	51, −8, −13
Angular gyrus	39	48, −53, 28
Cluster 2: Left hemisphere
Supramarginal gyrus	40	−55, −49, 28
Heschl's gyrus	41/42	−36, −30, 16
Superior temporal gyrus	22	−44, −34, 16
Middle temporal gyrus	21	−48, −58, 14
Cluster 3: Bilateral
Precuneus	7	8, −65, 25
Posterior cingulum	23	8, −37, 39
Postcentral gyrus	3	−20, −32, 61
Supplementary motor cortex	6	−8, −17, 49
Cluster 4: Right hemisphere
Superior frontal gyrus	9	20, 33, 39
Middle frontal gyrus	9	24, 33, 39
Inferior frontal gyrus (pars opercularis)	46	32, 17, 36
Cluster 5: Left hemisphere
Postcentral gyrus	3	−20, −32, 61
Precentral gyrus	4	−12, −29, 46
Cluster 6: Left hemisphere
Middle frontal gyrus	8	−28, 18, 43
Cluster 7: Left hemisphere
Paracingulate gyrus	32	−12, 48, 27
Superior frontal gyrus	9	−12, 52, 27
Cluster 8: Left hemisphere
Postcentral gyrus	3	−32, −21, 42
Cluster 9: Left hemisphere
Middle frontal gyrus	9	−24, 33, 35
Cluster 10: Right hemisphere
Postcentral gyrus	3	51, −14, 27

Bold type denotes the region with the maximum loading for that cluster.

Table IV.

Anatomical descriptions for each cluster (>5 voxels) of Component 4, with corresponding Brodmann's Areas and peak Talairach (XYZ) coordinates

Cortical region	Brodmann's areas	Max Talairach coordinate
Positive component loadings
Cluster 1: Bilateral
Medial frontal gyrus	6	−4, 1, 55
Superior frontal gyrus	6	−8, 10, 47
Precentral gyrus	6	−36, −5, 52
Inferior frontal gyrus	44	−51, 5, 26
Cluster 2: Left hemisphere
Inferior frontal gyrus	47	−36, 23, −5
Middle frontal gyrus	45	−44, 32, 13
Insula		−40, 12, 3
Cluster 3: Left hemisphere
Middle occipital gyrus	19	−28, −69, 26
Superior occipital gyrus	19	−20, −64, 33
Cluster 4: Right hemisphere
Middle frontal gyrus	46	32, 47, 16
Superior frontal gyrus	46	24, 48, 20
Cluster 5: Left hemisphere
Middle occipital gyrus	37	−48, −63, −7
Cluster 6: Left hemisphere
Supramarginal gyrus	40	−40, −41, 35
Negative component loadings
Cluster 1: Bilateral
Superior frontal gyrus	10	8, 60, 26
Medial frontal gyrus	9	−4, 56, 34
Anterior cingulum	32	4, 47, 9
Cluster 2: Left hemisphere
Angular gyrus	39	−48, −68, 37
Middle occipital gyrus	19	−40, −76, 33
Middle temporal gyrus	21	−55, −61, 22
Cluster 3: Right hemisphere
Angular gyrus	39	48, −60, 44
Middle temporal gyrus	21	55, −61, 21
Supramarginal gyrus	40	59, −49, 28
Cluster 4: Bilateral
Precuneus	23	4, −57, 32
Posterior cingulum	23	0, −53, 28
Cuneus		0, −69, 26
Cluster 5: Left hemisphere
Anterior cingulum	32	−16, 44, 16
Cluster 6: Left hemisphere
Superior frontal gyrus	46	−28, 59, 15

Bold type denotes the region with the maximum loading for that cluster.

Component 1

The component loadings mapped onto an M.N.I. structural image and the associated predictor weights plotted as a function of peristimulus time are displayed in Figure 1 and described in Table I. The pattern of activity suggests that this functional network involves the bilateral supramarginal/angular gyri (peaks in BAs 39, 40), with these clusters extending into the superior temporal gyrus (peak in BA 22) and the primary auditory cortex (Heschl's Gyrus; peaks in BAs 41/42 on the left). Other regions important for this component included bilateral superior/middle frontal gyri (peak in BA 9) and the bilateral posterior cingulate/precuneus (peaks in BA 7, 23).

Inspection of the predictor weights time series combined with the negative component loadings suggests that, relative to baseline, these regions showed decreased activation at the onset of the trial in a load‐dependent fashion. ANOVA revealed a highly significant time point × load interaction, F(18, 306) = 15.30, P < 0.001, η² = 0.47, suggesting that brain regions in this functional network are sensitive to increasing memory load. This was due to the magnitude of the time point effect increasing from 2 to 4, 6 and 8 letters, F(6, 102) = 10.72, P < 0.001, η² = 0.39; F(6, 102) = 42.31, P < 0.001, η² = 0.71; F(6, 102) = 29.00, P < 0.001, η² = 0.63; F(6, 102) = 31.06, P < 0.001, η² = 0.65, respectively. These significant time point effects demonstrate that the HRF shapes associated with this component were reliable for all load conditions. Considered within the context of the exclusively negative component loadings in Figure 1A, inspection of Figure 1C suggests that this pattern of decreased activation relative to baseline was confirmed with trial‐averaged BOLD signal for the regions displayed in Figure 1A.

Component 2

The component loadings mapped onto an M.N.I. structural image and the associated predictor weights plotted as a function of peristimulus time are displayed in Figure 2 and described in Table II. This functional network was characterized by activation in bilateral occipital gyri and primary visual cortex (peaks in BAs 17, 18, 19), bilateral precuneus (peak in BA 7), bilateral thalamus, bilateral medial/superior frontal gyri and precentral gyri (peaks in BAs 4, 6), and left postcentral/precental gyrus (peak in BAs 6, 3, 4).

Figure 2.

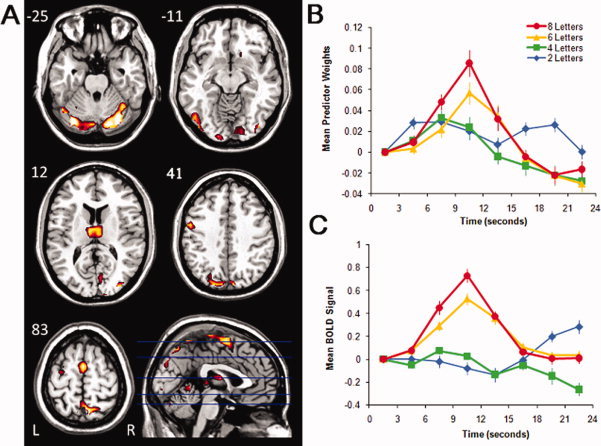
Images, plots of predictor weights, and plots of BOLD signal for Component 2. The dominant 5% of component loadings are displayed (A), with positive component loadings displayed in red (min = 0.26) and yellow (max = 0.41). (No negative component loadings passed this threshold.) The mean FIR‐based predictor weights are plotted as a function of peristimulus time in the right panel, top (B; error bars are standard errors). The predictor weights at the first point of peristimulus time are adjusted to zero, and all other values scaled accordingly for each subject, and therefore differ from % signal change by a constant term only. The mean BOLD signal extracted from the regions displayed in (A) are plotted as a function of peristimulus time in the right panel, bottom (C; error bars are standard errors). Axial slices are located at the following Talairach z axis coordinates: −25, −11, 12, 41, 83. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table II.

Anatomical descriptions for each cluster (>5 voxels) of Component 2, with corresponding Brodmann's Areas and peak Talairach (XYZ) coordinates

Cortical region	Brodmann's areas	Max Talairach coordinate
Cluster 1: Bilateral
Fusiform gyrus	19	28, −82, −13
Middle occipital gyrus	18	32, −89, 8
Lingual gyrus	17	16, −82, 13
Inferior occipital gyrus	18	24, −82, 13
Cluster 2: Bilateral
Precuneus	7	−8, −75, 48
Cuneus	19	−4, −80, 33
Cluster 3: Left hemisphere
Cerebellum		−36, −75, −16
Fusiform gyrus	19	−40, −74, −13
Middle occipital gyrus	19	−48, −70, −10
Inferior occipital gyrus	19	−44, −82, −6
Cluster 4: Bilateral
Medial frontal gyrus	6	0, 3, 59
Superior frontal gyrus	6	4, 7, 62
Middle frontal gyrus	6	32, −1, 55
Precentral gyrus	4	28, −16, 63
Cluster 5: Left hemisphere
Superior frontal gyrus	6	−32, −8, 63
Middle frontal gyrus		−32, −5, 59
Precentral gyrus		−32, −9, 59
Cluster 6: Left hemisphere
Middle frontal gyrus	6	−51, 2, 40
Postcentral gyrus	3	−51, −9, 45
Precentral gyrus	4	48, −9, 48
Cluster 7: Bilateral
Thalamus		−8, −11, 12
Cluster 8: Left hemisphere
Cuneus	17	−16, −93, −2
Lingual gyrus	18	−8, −93, 1
Cluster 9: Bilateral
Cerebellum		4, −47, 2
Cluster 10: Right hemisphere
Subcallosal gyrus/gyrus rectus	11	16, 19, −11
Putamen		16, 11, −7
Cluster 11: Left hemisphere
Cerebellum		−28, −59, −14
Cluster 12: Bilateral
Thalamus		0, −27, 5
Cluster 13: Left hemipshere
Superior temporal gyrus	22	−59, 11, −4

Bold type denotes the region with the maximum loading for that cluster.

Inspection of the predictor weights time series suggests that relative to baseline, these regions increased activity at the onset of the trial in a load‐dependent fashion, and this was confirmed by examining the trial‐averaged BOLD signal in Figure 2C for the regions displayed in Figure 2A. An ANOVA carried out on the predictor weights revealed a highly significant time point × load interaction, F(18, 306) = 11.92, P < 0.001, η² = 0.41, indicating that the magnitude and/or shape of the hemodynamic response was dependent on memory load. To interpret this interaction, we studied the effect of time point separately for each load. The magnitude of the time point effect increased over loads of 2, 4, 6, and 8 letters, F(2.4, 40.8) = 2.71, P = 0.07, η² = 0.14; F(6, 102) = 11.52, P < 0.001, η² = 0.40; F(6, 102) = 18.37, P < 0.001, η² = 0.52; F(6, 102) = 25.52, P < 0.001, η² = 0.60, respectively. These significant time point effects demonstrate that the HRF shapes associated with this component were reliable for the 4, 6, and 8 letter conditions.

Component 3

The component loadings mapped onto an M.N.I. structural image and the associated predictor weights plotted as a function of peristimulus time are displayed in Figure 3 and described in Table III. This functional network was dominated by positive component loadings in the bilateral occipital gyri and primary visual cortices (BAs 17, 18, 19), bilateral dorsal anterior cingulate gyri (peaks in BAs 32, 6), right dorsolateral prefrontal cortex (peak in BA 46), and bilateral supramarginal gyri and superior parietal lobes (peaks in BAs 7, 40).

Figure 3.

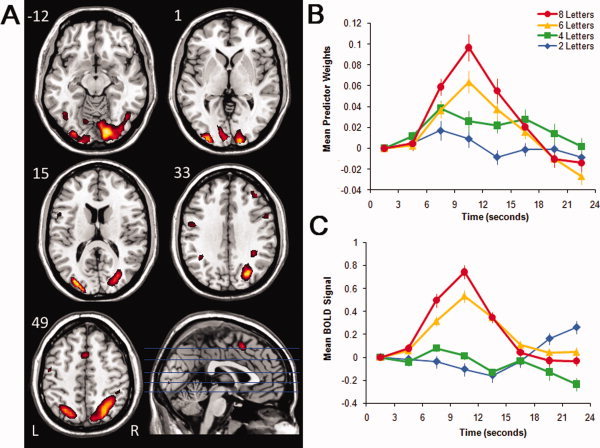
Images, plots of predictor weights, and plots of BOLD signal for Component 3. The dominant 5% of component loadings are displayed (A), with positive component loadings displayed in red (min = 0.26) and yellow (max = 0.41). (No negative components loadings passed this threshold). The mean FIR‐based predictor weights are plotted as a function of peristimulus time in the right panel, top (B). The predictor weights at the first point of peristimulus time are adjusted to zero, and all other values scaled accordingly, and therefore differ from % signal change by a constant term only. The mean BOLD signal extracted from the regions displayed in (A) are plotted as a function of peristimulus time in the right panel, bottom (C; error bars are standard errors). Axial slices are located at the following Talairach z axis coordinates: −12, 1, 15, 33, 49. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table III.

Anatomical descriptions for each cluster (>5 voxels) of Component 3, with corresponding Brodmann's Areas and peak Talairach (XYZ) coordinates

Cortical region	Brodmann's area	Max Talairach coordinate
Cluster 1: Right hemisphere
Lingual gyrus	18	16, −82, −6
Middle occipital gyrus	19	28, −69, 26
Superior lateral occipital cortex	7	24, −63, 51
Superior parietal lobule	7	32, −56, 51
Cluster 2: Left hemisphere
Middle occipital gyrus	19	−32, −81, 19
Superior lateral occipital cortex	18	−24, −84, 26
Occipital pole	17	−8, −93, −2
Intracalcarine cortex	17	−12, −81, 4
Cluster 3: Left hemisphere
Posterior inferior temporal gyrus	37	−44, −63, −14
Temporal occipital fusiform cortex	37	−40, −59, −14
Superior lateral occipital cortex	19	−44, −67, −13
Occipital fusiform gyrus	19	−36, −67, −17
Cluster 4: Left hemisphere
Superior parietal lobe	7	−28, −60, 47
Superior lateral occipital cortex	7	−20, −68, 48
Cluster 5: Left hemisphere
Precentral gyrus	4	−51, −6, 44
Cluster 6: Right hemisphere
Middle frontal gyrus	46	40, 40, 27
Cluster 7: Bilateral
Paracingulate gyrus	32	0, 14, 47
Posterior superior frontal gyrus	6	0, 14, 55
Cluster 8: Right hemisphere
Precentral gyrus	6	55, 9, 33
Inferior frontal gyrus (pars opercularis)	44	48, 9, 22
Cluster 9: Left hemisphere
Supramarginal gyrus	40	−40, −45, 32
Cluster 10: Left hemisphere
Inferior frontal gyrus (pars opercularis)	44	−51, 13, 18

Bold type denotes the region with the maximum loading for that cluster.

Inspection of the predictor weights time series suggests that relative to baseline, these regions increased in activity at the onset of the trial in a load‐dependent fashion, and this was confirmed by examining the trial‐averaged BOLD signal in Figure 3C for the regions displayed in Figure 3A. An ANOVA carried out on the predictor weights revealed a significant time point × load interaction, F(18, 306) = 25.97, P < 0.001, η² = 0.60, indicating that the magnitude and/or shape of the hemodynamic response was dependent on memory load. To interpret this interaction, we studied the effect of time point separately for each load. The magnitude of the time point effect increased over loads of 2, 4, 6, and 8 letters, F(6, 102) = 7.29, P < 0.001, η² = 0.30; F(6, 102) = 5.12, P < 0.001, η² = 0.23, F(6, 102) = 47.59, P < 0.001, η² = 0.74; F(6, 102) = 66.81, P < 0.001, η² = 0.80, respectively. These significant time point effects demonstrate that the HRF shapes associated with this component were reliable for all load conditions.

Component 4

The component loadings mapped onto an M.N.I. structural image and the associated predictor weights plotted as a function of peristimulus time are displayed in Figure 4 and described in Table IV. This functional network was dominated by positive component loadings in bilateral medial frontal gyri (peak in BA 6), right dorsolateral prefrontal cortex (peak in BA 46), left inferior and middle frontal gyrus (peaks in BAs 45, 47), bilateral precentral/postcentral gyri (peaks in BA 6), and left supramarginal gyrus (peak in BA 40). This component also showed negative component loadings in the bilateral medial/superior frontal gyri (peaks in BAs 9, 10), bilateral precuneus and posterior cingulate gyri (peak in BA 23), and bilateral superior temporal activation peaking in the angular gyri (peaks in BA 39).

Inspection of the predictor weights time series, interpreted alongside the component loadings displayed on the structural image in Figure 4A, suggests that relative to baseline, some regions increased and others decreased activation at different points in the working memory trial, in a load‐dependent fashion. An ANOVA carried out on the predictor weights revealed a significant time point × load interaction, F(18, 306) = 3.95, P < 0.001, η² = 0.19, indicating that the magnitude and/or shape of the hemodynamic response was dependent on memory load. To interpret this interaction, we studied the effect of time point separately for each load. The magnitude of the time point effect increased over loads of 2, 4, 6, and 8 letters, F(6, 102) = 6.43, P < 0.001, η² = 0.27; F(6, 102) = 5.36, P < 0.001, η² = 0.24; F(6, 102) = 12.30, P < 0.001, η² = 0.42; F(6, 102) = 17.66, P < 0.001, η² = 0.51, respectively. These significant time point effects demonstrate that the HRF shapes associated with this component were reliable for all load conditions. Inspection of Figure 4C,D suggests that this pattern of increased and decreased activation relative to baseline can be confirmed with trial‐averaged BOLD signal for the regions displayed in Figure 4A.

DISCUSSION

FIR‐CPCA was used to examine the temporal dynamics of functional networks involved in verbal working memory. This technique involved performing principal component analysis on the variation in BOLD signal that is predictable from a FIR model of the stimulus presentation timing. Four components were extracted, all of which peaked at approximately 10 s following trials onset. Two of the components sustained this peak for approximately 3 s (Components 1 and 4), and the other two did not (Components 2 and 3). All components showed statistically significant sensitivity to the memory load manipulation and reliable HRF shapes.

It has recently been discovered that a wide range of effortful cognitive tasks consistently lead to not only increases in activity in fronto‐parietal brain regions but also concomitant decreases in activity in ventro‐medial brain regions. These anticorrelated networks have been coined the task‐positive and task‐negative network, respectively [Fox et al., 2005]. The current network‐focused analysis method emphasized the possibility of an important interplay between the two anticorrelated functional networks. Interestingly, most activations and deactivations observed in the current set of results can understood within this context.

The exclusively negative component loadings on Component 1, combined with the BOLD signal changes depicted in Figure 1C, suggest that activation decreased on initiation of a delayed recognition trial. These deactivations included some task negative regions, such as posterior cingulate/precuneus and superior medial prefrontal cortex. Also observed for this component was the coordinated decrease in bilateral primary auditory cortex activity that could relate to reduced activation during inner speech [Buchsbaum et al., 2005; Frith et al., 1991] or a more general phenomenon whereby task‐irrelevant primary sensory cortex (with visual cortex being task‐relevant) is deactivated during task performance [Laurienti et al., 2002; Shulman et al., 1997]. The effect size associated with Component 1 was smallest for the load 2 condition; however, it did not exhibit clearly linearly increasing load dependent (de)activity. Together, the regions and patterns of activity for this component are consistent with deactivations found specifically in working memory paradigms, as well as deactivations related to effortful cognitive processing, more generally.

Components 2 and 3 were dominated by regions typically involved in effortful, attention demanding cognitive tasks in addition to those more specific to working memory, and both showed clear load dependence, with linearly increasing effect sizes. Several of the neural regions involved in both Components 2 and 3 appear consistent with the task‐positive functional network, such as dorsal anterior cingulate, postcentral/precentral gyri, and dorsolateral prefrontal cortex. Load‐sensitive involvement of fronto‐parietal regions is also consistent with the multiple demands network of Duncan and Owen [ 2000] in which these regions function as a network during the performance of a variety of attention demanding tasks. Some of the observed regions have, however, been tied to more specific roles in working memory. One of these, the fusiform gyrus, is considered sensitive to the encoding and short‐term maintenance of letter strings and words [Fiebach et al., 2006]. The superior parietal lobule (Component 3) may play a critical role in both maintenance and manipulation of verbal information in working memory, as demonstrated by a recent transcranial magnetic stimulation study [Postle et al., 2006], whereas the intraparietal sulcus is a candidate for capacity‐limited storage in (visual) working memory [Todd and Marois, 2004]. The posterior middle frontal gyrus (Components 2 and 3), on the other hand, has been associated with control processes recruited during working memory [Derrfuss et al., 2004; McNab and Klingberg, 2008]. The visual cortices (BA 18, 19) were also strongly activated but presumably reflect perception of visually presented stimuli during the initial phase of each trial.

Component 4 was also strongly load dependent and involved aspects of both the task positive and task negative networks, and the fronto‐parietal network. Relative to Components 2 and 3, the task‐positive aspects of Component 4 did not involve primary visual cortex regions, and included left inferior prefrontal and right dorsolateral prefrontal activations that were more anterior than the like‐lateralized activations in Components 2 and 3. Relative to Component 1, the task‐negative aspects of Component 4 were more anterior and dominant for the medial frontal regions and more posterior and dominant for the posterior cingulate and angular gyrus aspects.

It is perhaps important to comment upon the small amount of variance accounted for by Component 4. Indeed, one might expect the task‐positive processes sustained into the delayed recognition trial to be more dominant, given that there are a number of processes related to memory capacity limits, retrieval from memory, decision making, and response preparation/execution required by the task, but it may be precisely the variability across these different processes which leads to the relatively minor signal reflected by Component 4. Alternatively, or perhaps in addition to these reasons, there could have been substantial individual differences within any of these processes resulting in increased variability in the evoked signal. Some cognitive processes in which such individual differences have been noted are proactive interference [Feredoes et al., 2009], memory capacity [Todd and Marois, 2005], and the scanning of the contents of memory [Oztekin et al., 2009]. These considerations of variability across subjects may help to constrain the interpretation of the processes represented by the other components, in that they might be representing those processes which are less susceptible to individual differences.

In sum, these networks revealed by FIR‐CPCA are consistent with previous findings from both the working memory literature and more general cognitive investigations. The identification of multiple networks simultaneously is, however, a unique observation, and one would predict that with more targeted manipulation of the different task stages, for example, the contribution of each network could be more thoroughly explored.

Interpretation of Component Time Series

All four components displayed peak activation approximately 10–11 s after trial onset, which is precisely the peak expected for a HRF in response to a 3‐s encoding stage. However, only two of the four components sustained this peak activity, both for approximately 3 s (Components 1 and 4). Although all components are likely invoked at encoding, the sustained peak components are more likely to be involved in both the encoding and delay period. Correspondingly, these sustained peak components may be more representative of the regions involved in encoding and maintenance over a short period [Postle, 2006].

Role of HRF shapes in FIR CPCA

As was mentioned in the introduction, FIR models are preferable to HRF models in CPCA for a number of reasons, one of which is avoidance of restricting the variance in GC to scaled versions of the HRF model shapes. Given this, clarification may be needed to explain our reasons for revisiting HRF models at the stage of component rotation. In this context, it is important to distinguish between the three CPCA stages of analysis [Hunter and Takane, 2002, pp 107–112]: (1) the external analysis, involving multivariate multiple regression, depicted in Eqs. 1 and 3, (2) the internal analysis, involving singular value decomposition, depicted in Eqs. 2 and 4, and (3) component rotation, depicted in Eqs. (5), (6), (7). The internal analysis is exploratory in nature and does not involve use of a FIR or HRF model. In contrast, the variance captured in the external analysis is completely determined by the choice of model, such that any variation in BOLD signal that is not captured by the model (e.g., that not conforming to a scaled version of the HRF model shapes) would be excluded for the subsequent internal analysis, thus leading to the preference for the less restrictive FIR model. This can be contrasted with the component rotation stage, which, as is clear from Eqs. 5–7, involves redistributing variance by creating weighted combinations of the existing columns of VD, U, and P matrices. This allows new combinations of the patterns of variance contained in the components, leading to new interpretations, but does not exclude certain patterns of variance as does the external analysis, or create new patterns of to‐be‐redistributed variance. In fact, all rotations of the component solution are equally valid, in that they do not change the adequacy of the solution; that is to say, the percentage of variance in GC accounted for by the component solution will not change with rotation methodology. Thus, the function of the HRF shapes at the rotation stage are to emphasize HRF‐shaped patterns that already exist in the component solution, but not to increase or decrease the percentage of variance accounted for by the component solution.

Comparison to Prior Analyses

Our original CPCA analysis of these data [Woodward et al., 2006] used an HRF design matrix in G, which modeled stage‐specific hemodynamic responses as idealized BOLD responses to stimulus presentations. The current FIR model method allowed the following to be demonstrated: (1) a load‐dependent interpretation for a previously uninterpretable component; namely, a network characterized by reduced activation likely involved in encoding and delay period processes (Component 1); (2) a detailed display of the estimated hemodynamic response associated with each component; (3) elimination of the risk of interpretative errors linked to inaccurately labeled or inaccurately derived hemodynamic response models of correlated task stages; and (4) elimination of the risk that BOLD activity not conforming to the modeled synthetic HRF shape is either misattributed to correlated task stages or is overlooked by the analysis procedure.

As a concrete example of how the FIR‐CPCA analysis can eliminate the risk of certain interpretative errors, we revisit our previous article [Woodward et al., 2006] where we reported evidence for a “load‐dependent, reciprocal relationship” between the encoding and delay networks that involved the occipital cortex (based on a component similar to what is referred to here as Component 4). In light of the results obtained from the FIR analysis, our previous interpretation appears erroneous. The previously reported component displayed negative loadings in occipital regions, negative loadings in task‐negative regions, and positive loadings in task‐positive regions. The negative loadings on occipital regions did not replicate in the current FIR analysis, although the task‐negative and task‐positive loadings did. The FIR analysis clarifies that both the occipital regions and the task positive network in fact increased together with the onset of encoding, but the visual cortex activation (Components 2 and 3) drops off earlier than the task‐positive activations on Component 4, producing the correlation with the task‐negative network observed in our previous paper. This suggests that the previously reported negative component loadings in occipital regions were due to spurious correlations between a decrease in occipital cortex due to termination of the visual display, and task‐related deactivations associated with the task‐negative network. The emergence of these predictor weights and the misinterpretation of occipital decreases associated with the termination of the encoding display as deactivations associated with the delay period (and reciprocally related to encoding) appear to be interpretational errors partly caused by the false precision associated with using labels attached to HRF models of task stages.

Comparison of CPCA to Related Multivariate Methods

There are a number of previously proposed multivariate methods for analyzing fMRI data that examine the relationship between two sets of variables (X and Y denoting stimulus information and BOLD signal, respectively), such as PLS [McIntosh et al., 2004], CVA [Strother et al., 2004], and MLM [Worsley et al., 1997]. Although these approaches are similar to CPCA and are mathematically equivalent under some conditions, there are some important differences.

One of the main considerations when comparing CPCA to other multivariate approaches relates to the fit between the statistical method and the logic underlying fMRI experiments, with respect to how the X and Y matrices are placed on the predictor and/or criterion sides of the general linear model. Most fMRI experiments, such as the current one, are designed to determine how experimental design and stimulus timing (modeled in X and treated as a fixed effect) affects the distribution of the brain state (as measured by the BOLD signal Y); therefore, information about the stimulus presentations should be considered a set of predictor variables and the BOLD signal a set of criterion variables. Regression analysis specifically analyzes the conditional expectation of Y given X, that is to say, E(Y | X) = ∫ (Yp(Y | X))dX, where p(Y | X) is the (conditional) distribution of Y given X. Correspondingly, for CPCA, X is placed on the predictor side, Y is placed on the criterion side, and the objective is to find a consequence of X, which is, in turn, a cause for Y, thereby providing a natural fit to the logic underlying typical fMRI experimental designs. For CPCA (or any linear regression analysis), E(Y | X) is assumed to be linear. In other contexts, however, the motivation may be to predict stimulus condition X from the brain state Y, as is the case with mind‐reading paradigms [Hansen, 2007], for which discriminant function analysis would be a more appropriate analytic method (review of this class of fMRI experiments is outside the scope of the current discussion, but please refer to Haynes and Rees [ 2006]).

In contrast to CPCA, PLS places both X and Y on the criterion side and seeks to find a common cause for both. The mathematical technique employed by PLS is commonly referred to as least squares interbattery factor analysis [Tucker, 1958], where it is assumed that there is a common cause for the two sets of variables and their joint distribution is analyzed [Hansen, 2007]. This is the methodology of choice under conditions where neither X nor Y are controlled. However, it should be noted that PLS reduces to a special case of CPCA when X is column‐wise orthonormal.

Despite this mathematical equivalence, the current application of CPCA would not give the same results as the PLS software package [McIntosh et al., 2004] due to important differences in the matrices submitted to the analysis. For example, in PLS, the BOLD signal matrix referred to above as Y is converted to a percent signal change (from trial onset) and reorganized into a matrix that the authors referred to as M. Each row of the M matrix contains the (percent‐signal‐change converted) BOLD signal from prespecified peristimulus time points, averaged over all occurrences of the condition of interest, computed separately for each subject and condition. Thus, unlike its CPCA counterpart Z, M will not consider BOLD signal from the entire time series if the specified number of scans comprising peristimulus time does not cover all collected scans due to the experiment design. (The CPCA method of using the values 0 and 1 in G to contrast peristimulus time against other scans in Z does not have the same effect as the PLS method of selecting only scans in peristimulus time for inclusion in M. G is used as a set of binary predictor variables in a multivariate multiple regression, and the actual values are arbitrary and do not affect results.) An additional difference involves the matrix representing the experimental design, referred to above as X, but referred to as C by the authors. Unlike its CPCA counterpart G, the PLS‐based C does not contain a model of the hemodynamic response, but instead contains codes that contrast the averaged BOLD signal from the conditions represented in the rows of M.

CVA is a special case of canonical correlation analysis, where it is assumed that the two sets of variables are causing a common factor, typically arising when X and Y are causing something in common. As such, CVA places both X and Y on the predictor side and seeks to find a common consequence of both. In the case where Y is column‐wise orthonormal or X is a matrix of dummy variables indicating class labels, CVA reduces to CPCA. However, in part due to the preliminary PCA performed on the BOLD signal, CVA as suggested by Strother et al. [ 2004] would not match the results provided by the current application of CPCA.

In MLM, as in CPCA, X is placed on the predictor side and Y is placed on the criterion side, and the objective is to find a consequence of X, which is, in turn, a cause for Y. In terms of mathematical operations, the main difference between MLM and CPCA lies in the estimation method they use. MLM uses a heuristic estimation method, which is claimed to be robust, and leads to an analytical significance testing procedure [Worsley et al., 1997] and takes into account possible nonzero covariances among the rows of Z represented by a matrix S. The estimation method used in CPCA is consistent with redundancy analysis [Lambert et al., 1988] and, in the form utilized here, it ignores the covariances among the rows of Z; however, this could be remedied by taking C = (G′S ⁻¹ G)⁻¹ G′S ⁻¹ Z as the rank‐free estimate of regression weights (rather than assuming S = I), where S is the covariance matrix among the rows of Z. If S is known exactly (i.e., when the population covariance matrix is known), this gives the best linear unbiased estimator (BLUE) of C. S usually has to be estimated, however, and a very good estimate of S must exist in order for the above estimator to work well, and this is also the case for MLM. In general, it is difficult to determine which estimation method (MLM or CPCA) is uniformly better than the other in a small sample and this question must be addressed empirically in future research.

As a final and very important point of comparison, CPCA provides a more general mathematical framework than PLS, CVA, or MLM, in that it allows the data to be decomposed into sources of variance predictable from row information (as does PLS, CVA or MLM), but also from column information, contrasts of row and column information, all combinations thereof, as well as the variance not explained by row or column information, with components being computed on any or all of those sources of variance [Takane and Hunter, 2001; Takane and Shibayama, 1991]. The full CPCA model is as follows:

(8)

With the H matrix providing constraints on the voxels coded in the columns of Z, and GMH is variance in Z predictable from the interaction between G and H. We are currently developing applications of CPCA to use the G and H matrices simultaneously to analyze fMRI data. Candidates for the H matrix are anatomical networks of theoretical interest, such ventral/dorsal networks, lateralization of cognitive functions, or any a priori neural networks of interest.

CONCLUSIONS

This FIR‐CPCA analysis methodology provided a method for assessing functional connectivity between neural regions engaged by a verbal delayed recognition task. This approach allowed (1) determination of multiple functional networks involved in working memory, (2) estimation of the pattern of BOLD changes associated with each functional network over peristimulus time points, (3) a statistical test of the reliability of the HRF associated with each component; and (4) a statistical test of the degree to which experimental manipulations (in this case working memory load) affects each functional network. Each of the components included brain regions consistent with previous studies on the stages involved in working memory delayed recognition, but also included regions involved in the putative task‐positive/task‐negative anticorrelated functional networks [Fox et al., 2005] and the multiple demands network [Duncan and Owen, 2000]. The ability to visualize the pattern of activity of a correlated network over time and its sensitivity to experimental manipulations are suited particularly for investigation of multiple‐stage cognitive tasks.