Linearity of the fMRI response in category‐selective regions of human visual cortex

Abstract

The goal of this study was to determine the linearity of the blood oxygen level‐dependent (BOLD) response, as measured by functional magnetic resonance imaging (fMRI), in category‐selective regions of human visual cortex. We defined regions of the temporal lobe that were selective to faces (fusiform face area, FFA) and places (parahippocampal place area, PPA). We then determined the linearity of the BOLD response in these regions to their preferred and nonpreferred stimuli. First, we tested the principle of scaling. As we increased the visibility of the stimulus, there was a corresponding linear increase in the fMRI signal in the FFA and PPA to their preferred stimulus (face and place, respectively). In contrast, responses in the FFA and PPA to the nonpreferred stimulus did not conform to the principle of scaling. Next, we asked whether the fMRI response in these regions of visual cortex conformed to the principle of additivity. To assess this, we determined whether the response to a long stimulus block could be predicted by adding the response to multiple shorter duration blocks. Although the fMRI response in the FFA and PPA was generally linear to the preferred stimulus, a more nonlinear response was apparent to the nonpreferred stimulus. In conclusion, the linearity of the BOLD response in the human ventral visual pathway varied across cortical region and stimulus category. This suggests that measures of linearity may provide a useful indication of neural selectivity in the brain. Hum Brain Mapp, 2009. © 2008 Wiley‐Liss, Inc.

INTRODUCTION

Generally, cognitive neuroscience aims to relate changes in neural activity with cognitive states. Neuroimaging techniques such as fMRI provide a potentially powerful tool for measuring neural activity. However, determining the exact relationship between neural events and cognitive or perceptual states using fMRI is complicated by the spatial and temporal characteristics of the BOLD response. fMRI typically measures neurally evoked haemodynamic changes by means of the blood oxygenation level‐dependent (BOLD) response. An increase in neural activity leads to a local increase in blood flow and volume. The resultant change in deoxyhaemoglobin concentration, due to increased oxygen delivery, causes changes in the T2*‐weighted magnetic resonance signal [Ogawa et al., 1990]. Thus, although neural responses typically occur within tens of milliseconds following sensory stimulation, the first observable changes in the BOLD signal are in the order of seconds.

The relationship between neural activity and the BOLD response is often approximated to that of a linear system [Friston et al., 1995]. This means it conforms to certain properties such as scaling and additivity. The principle of scaling is that the output should be directly proportional to the input; if the amplitude increases by a factor of two, the amplitude of the output will also increase by the same factor. Additivity is concerned with the integration of individual responses over time. Thus, the output of a system to more than one input is equal to the sum of the responses to the individual inputs had they occurred in isolation. It is important to note that this differs from other definitions of linearity in which it is defined by the fit to a straight line (i.e., whether two variables are linearly related).

Evidence for the linearity of the BOLD response was first reported by Boynton et al. [1996] using simple visual stimuli. To evaluate the principle of scaling, they varied the contrast of a checker board pattern and found that the amplitude of the MR response in visual cortex was proportional to the contrast of the stimulus. To test for additivity, they asked whether the response to a longer duration stimulus could be predicted by the sum of multiple shorter duration stimuli. They found that, in general, the response to a stimulus could be predicted linearly by the sum of the responses to shorter duration stimuli. However, they also found that the response to short duration stimuli overestimated the measured response at longer durations. A similar nonlinearity in response can occur when two visual events occur in rapid succession, with the response to the second stimulus being less than if it was presented in isolation [Dale and Buckner, 1997; Huettel and McCarthy, 2000]. However, with longer ISIs (>6 s), the BOLD response can be predicted by the linear addition of two isolated events. Subsequent work in human visual [Gu et al., 2005; Hoge et al., 1999; Miezin et al., 2000; Vazquez and Noll, 1998], motor [Bohning et al., 2003; Glover, 1999; Miller et al., 2001], and auditory cortex [Glover, 1999; Rees et al., 1997; Soltysik et al., 2004], as well as macaque visual cortex [Guatama et al., 2003; Logothetis et al., 2001] has largely confirmed that variance in the BOLD response in primary sensory and motor regions can be largely explained by a linear model.

The approximate linearity of the BOLD response found in primary visual areas contrasts with reports of nonlinear responses in the higher visual areas. For example, Avidan et al. [2002] found that the response in category‐selective regions of ventral visual stream did not show a linear relationship with the contrast of the image. Similarly, Mukamel et al. [2004] failed to find a linear relationship between the BOLD response and the rate at which stimuli were presented. It would appear that the results from studies assessing linearity in early visual cortex may not be applicable to cortical regions higher in the visual processing stream. Indeed, other studies have found that the linearity of the BOLD response can vary in different cortical regions [Birn et al., 2001; Boynton and Finney, 2003; Soltysik et al., 2004].

The goal of this study was to further explore the linearity of the BOLD response to complex objects in human visual cortex. This issue is particularly important, given the large body of fMRI literature concerned with higher‐order visual cortex. We took advantage of the category selectivity found in the inferior temporal lobe to determine the linearity of the BOLD response to preferred and nonpreferred stimuli. For example, the fusiform face area (FFA) is typically defined by a higher response to faces compared with a variety of nonface objects [Kanwisher et al., 1997], whereas the parahippocampal place area responds more to images of buildings and scenes [Epstein and Kanwisher, 1998]. Our specific hypothesis was that the BOLD response in a region would be more linear to its preferred stimulus compared to its nonpreferred stimulus.

METHODS

Subjects

Ten participants participated in the study, (five females; mean age, 24). All observers had normal or corrected to normal visual acuity. Written consent was obtained from all subjects and the study was approved by the York Neuroimaging Centre Ethics Committee. Subjects lay supine in the magnet bore and viewed stimuli (∼8° × 8°) back‐projected onto a screen located inside the bore of the scanner, ∼57 cm from their eyes.

Imaging Parameters

All experiments were carried out using a GE 3 Tesla HD Excite MRI scanner at the York Neuroimaging centre (YNiC) at the University of York. A Magnex head‐dedicated gradient insert coil was used in conjunction with a birdcage, radio‐frequency coil tuned to 127.4 MHz. A gradient‐echo EPI sequence was used to collect data from 20 contiguous axial slices covering the occipital and temporal lobes (TR 2 s, TE = 30 ms, FOV 240 mm², in plane resolution 1.875 × 1.875 mm, slice thickness 4 mm). Statistical analysis of the fMRI data was carried out using FEAT (http://www.fmrib.ox.ac.uk/fsl). The initial 8 s of data from each scan were removed to minimize the effects of magnetic saturation. Motion correction was carried out using MCFLIRT (http://www.fmrib.ox.ac.uk/fsl), followed by spatial smoothing (Gaussian, FWHM 5.0 mm) and temporal high‐pass filtering (cutoff, 0.01 Hz). Z‐statistic images based on the contrast between different events were generated using resel thresholding (P < 0.05).

Experiment 1: Localizer Scan

To discriminate regions of visual cortex that are selectively activated by images of faces and places, a localizer scan was carried out for each subject. Each scan contained 15 stimulus blocks. Each block contained images from one of three different object categories: (i) faces, (ii) places (buildings, indoor and outdoor scenes) or (iii) phase scrambled images of faces and places. Photographs of unfamiliar faces were taken from a database of the Psychological Image Collection at Stirling (PICS: http://pics.psych.stir.ac.uk). Phase scrambled images were Fourier randomized versions of the face and place images. Each 10 s stimulus block contained 10 images with each image being presented for 1 s. Each stimulus condition was repeated five times in a counterbalanced block design. Stimulus blocks were separated by periods of fixation when a white cross on a gray screen was viewed for 10 s. During each stimulus block, subjects were instructed to perform a target detection task, with two or three images in each block containing a red dot. Subjects were required to respond, with a button press, as soon as they saw the image containing the target.

Face selective regions of interest (ROI) were determined by the contrast face > place. Place selective ROI were determined by the contrast place > face. These ROI were combined across hemispheres for each individual. The time series of the resulting filtered MR data at each voxel was converted from units of image intensity to percentage signal change by subtracting and then normalizing by the mean response of each scan ([x − mean]/mean × 100). Individual stimulus blocks were normalized by subtracting every time point by the zero point for that stimulus block. The normalized data were then averaged to obtain the mean time course for each stimulus condition. All further analyses were carried out on the mean time course of voxels. Repeated measures ANOVAs were used to determine significant differences in the response to each stimulus condition.

Experiment 2: Scaling

The principle of scaling was assessed independently for face and place stimuli across two separate scans. The strength of the stimulus was varied by randomizing the phase of each 2D frequency component in the image, while keeping the power of the components constant. The phase randomized images were then combined with the original unscrambled images to varying extent. A phase coherence of 50% therefore means the original image and scrambled image contributed equally in the production of the new image. The phase coherence of each block was either 20, 40, 60, or 80%. An example of the stimuli is shown in Figure 1. Each scan (for face and place stimuli separately) consisted of 36 blocks relating to nine repetitions of each of the four levels of phase coherence. The order of blocks was counterbalanced such that each set of four blocks (one super‐block) contained one of each of the phase coherence levels. The presentation order within each super‐block was pseudo‐randomized such that each phase coherence level was seen at each super‐block position (i.e., from position 1–4) at least twice (see Supp. Info. Fig. 1). Each stimulus block lasted 8 s and contained eight stimuli that were presented for 1 s. Stimulus blocks were preceded by a 1 s red fixation‐cross to alert the participant of an oncoming block, and were followed by a 10 s gray‐screen of equal average luminance to the stimulus blocks (fixation period). During the stimulus blocks, participants were required to make a button‐response when a red‐dot appeared on any of the stimuli. There were two to three red‐dots per stimulus block. Following data preprocessing, normalized averaged time‐series for each condition (20, 40, 60, 80%) in each ROI in each participant were extracted from the filtered MR data. For each of these time‐series the peak amplitude was calculated as the mean of the three highest‐amplitude consecutive time‐points.

Figure 1.

Examples of face and place images at different levels of phase coherence (%).

The scaling study was accompanied by a behavioral study assessing participants' recognition accuracy at varying levels of phase coherence to both face and place stimuli. Subject performed two blocks of trials (faces and places). Each block contained 120 trials. Each trial was preceded by a 300 ms fixation cross. The first image was then presented for 300 ms, followed by a 500 ms fixation cross. The second image was then presented for 300 ms, followed by a fixation cross that remained on screen until participants had responded. The two images in each trial differed in phase coherence. One of the images was at 0% phase coherence, whereas the other (target) was at one of six levels of phase coherence (5, 15, 20, 40, 60, 80%). The task was a 2AFC (2 alternative forced choice) with participants required to make two responses: (i) whether the target image (nonscrambled) was presented first or second, (ii) whether the target image was male or female (face block) or an indoor or outdoor scene (place block). The first response was designed to measure the participants' ability to detect a stimulus (face or place) from noise (detection), the second to make a within‐category discrimination. The assignment of keys to responses was varied between participants to balance any possible leftward or rightward biases. Equal numbers of male and female (indoor and outdoor) images were used in each condition; equal numbers of trials showed the target image first or second in each condition. A psychometric function was fit to the data for each subject and a threshold set at 75% correct.

Experiment 3: Additivity

The principle of additivity was assessed over two scans (face and place) by measuring the response to varying durations of stimulus presentation. Each scan (faces and places) contained 40 blocks. The durations of each block were: 2, 4, 8, or 16 s. Each condition was repeated 10 times in a counterbalanced block design for both face and place stimuli. The order of blocks was counterbalanced such that each set of four blocks (one super‐block) contained one of each of the four block durations. The presentation order within each super‐block was pseudo‐randomized such that each block duration was seen at each super‐block position at least twice (see Supp. Info. Fig. 1). In each stimulus block, stimuli were presented for 1 s at a rate of 1 Hz. Stimulus blocks were followed by a gray‐screen with a fixation cross (for 10 s). Participants were required to make a button‐press response when either a male (or female) face or an indoor (or outdoor) place was present. The target image (male/female, indoor/outdoor) was varied across participants. Face blocks always contained equal numbers of male/female images; place blocks always contained equal numbers of indoor/outdoor images. Thus, participants were responding to 50% of the presented images in each block. Each stimulus was repeated six times and presentation order was randomized across conditions and blocks.

Following data preprocessing, normalized averaged time‐series for each condition (2, 4, 8, 16 s) in each ROI in each participant were extracted from the filtered MR data. For each individual the 2 s response was used to predict the 4, 8, and 16 s response; the 4 s response was used to predict the 8, and 16 s response; and the 8 s response was used to predict the 16 s response. These predicted responses were the summation of the shorter measured responses with a temporal offset. For example, the 4 s response was predicted by the summation of two 2 s responses with a 2 s temporal offset.

For each predicted and measured time‐series the peak amplitude was calculated as the mean of the three highest‐amplitude consecutive time‐points. Amplitude ratios (AR‐predicted response amplitude/measured response amplitude) were calculated between the measured 16 s response, and the 16 s response as predicted by the measured 2, 4, and 8 s response for each participant. An AR of 1 denotes a linear response; an AR‐value of greater than 1 denotes an overprediction of response. Regression analyses between the measured and predicted (time‐series) response were also carried out using the least squares method between the measured 16 s response, and the 16 s response as predicted by the measured 2, 4, and 8 s response for each participant.

RESULTS

Experiment 1: Localizer Scan

Figure 2 shows regions in the inferior temporal lobe that showed face‐ or place‐selective activity. The mean MNI coordinates, together with mean cluster size across participants are shown in Table I. A region in the parahippocampal gyrus (PPA) responded more to viewing of places than viewing of faces [Epstein and Kanwisher, 1998], whereas a region in the fusiform gyrus (FFA) responded more to viewing of faces than viewing of places [Kanwisher et al., 1997]. Each region was defined separately for each individual and all further analyses were performed on the mean time courses of voxels in these ROI.

Figure 2.

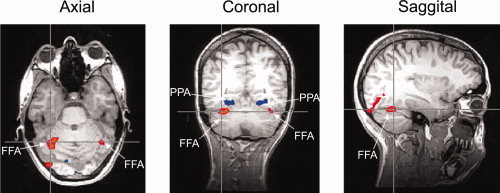
The location of the fusiform face area (FFA) and parahippocampal place area (PPA) in one subject. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table I.

Mean MNI coordinates and cluster size for each region of interest

Region		Coordinates			Cluster size (cm3)
		x	y	z
FFA	L	−34	−62	−26	0.42
	R	32	−64	−24	0.71
PPA	L	−24	−66	−16	1.34
	R	22	−66	−16	1.44

Experiment 2: Scaling

Figure 3 shows the mean amplitude of the fMRI response at each phase coherence in the different ROI. For scaling to hold, the increase in peak amplitude should be proportional to the increase in phase coherence; for example, peak amplitude at 40% coherence should be twice the amplitude at 20%. This should be reflected in a slope of the regression line (β) being close to unity. The data clearly shows that increasing the strength (phase coherence) of the preferred stimulus resulted in a systematic increase in the BOLD response. In contrast, the response to the nonpreferred stimulus shows a much lower effect of increased stimulus strength. We calculated the regression for each participant and found a significant linear component for faces in the FFA [β = 0.75, t(8) = 7.18, P < 0.001; R ² = 0.65, t(8) = 6.08, P < 0.001] and places in the PPA [β = 0.92, t(8) = 32.94, P < 0.001; R ² = 0.88, t(8) = 41.44, P < 0.001]. Despite the response to nonpreferred stimuli in both the FFA and PPA appearing to diverge from linearity, a significant linear component was also seen for faces in the PPA [β = −0.40; t(8) = 2.48, P < 0.05; R ² = 0.36, t(8) = 3.13, P < 0.05] and places in the FFA [β = 0.51, t(8) = 3.46, P < 0.01; R ² = 0.43, t(8) = 4.23, P < 0.01]. Note, however, that the response to faces in the PPA actually shows a significant decrease in BOLD response as phase coherence increases. Importantly, the regression analyses demonstrated significantly greater β and R ² values [β: t(8) = 3.28, P < 0.05; R ²: t(8) = 2.73, P < 0.05] for preferred than nonpreferred stimuli. The relationship between BOLD response and phase coherence would therefore appear to be more linear for preferred than nonpreferred stimuli in both the FFA and PPA.

Figure 3.

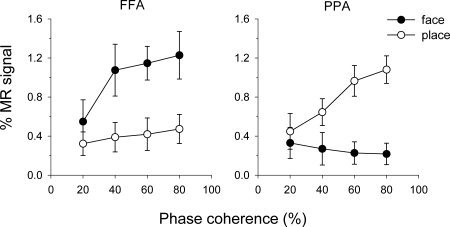
Mean peak amplitudes for face and place images in the FFA and PPA at 20, 40, 60, and 80% phase coherence. Error bars represent 95% confidence intervals.

These data suggest the linearity of the BOLD response is dependent upon both stimulus‐type and region. To explicitly test this hypothesis, the mean amplitude data were entered into a 2 × 2 × 4 (Stimulus‐type × Region × Coherence‐level) within‐subject ANOVA, revealing a significant Stimulus‐type × Region × Coherence‐level interaction, F(1.8, 15.9) = 96.93, P < 0.001 (Greenhouse‐Geisser corrected). Within the FFA, faces showed a significantly greater increase in amplitude across phase coherence than places, F(2.6, 23.1) = 11.98, P < 0.001. Within the PPA, the increase in amplitude across phase coherence for places was significantly greater than the decrease seen for faces, F(2.5, 22.9) = 30.61, P < 0.001.

The aforementioned data confirm the prediction that there is a significant linear component in the relationship between phase coherence and BOLD response in the FFA and PPA to both faces and places. On inspection of Figure 3 however the increase in BOLD response to faces in the FFA looks to diverge from a strictly linear relationship. Specifically, the BOLD response looks to increase more rapidly between 20 and 40% phase coherence than between 40 and 80%. It is therefore possible that the data also contain a significant nonlinear component (i.e., that the unexplained variance from the linear regression analyses may have structure). To address this concern we fitted the data to an exponential function (1 − e ^−x) that could plausibly capture the nonlinear trend seen for faces in the FFA at the same time as keeping the number of estimated parameters equal to the linear regression analyses. Although such a function was able to capture a significant proportion of the variance across all stimuli and regions [β > 0.40, R ² > 0.36; t > 2.5, P < 0.05], it did not explain a greater proportion of variance than the linear fits (t < 2.1, P > 0.09). Therefore, if a significant nonlinear component is present within the current data, it is not sufficiently captured by such a function1.

During the scans, subjects had to respond to a red dot that appeared on about 30% of images. Subjects were very accurate in responding to the target during face and place scaling scans (μ = 99%, σ = 0.02). Accuracy was not significantly affected by phase coherence in the face scans [F(3, 27) = 0.92, P > 0.05] or place scans [F(3, 27) = 1.33, P > 0.05]. We also measured the reaction time in the different conditions. There was no effect of phase coherence on reaction times in the place scans [F(2, 27) = 0.38, P > 0.05], but there was an effect in face scans [F(3, 27) = 6.41, P < 0.05]. Post hoc tests revealed significantly faster reaction times to red‐dot presentation at 60% than 80% phase coherence; no other contrasts revealed a significant effect.

In an independent behavioral study, we compared detection and within‐category discrimination accuracy for the phase‐scrambled images. Figure 4 shows that accuracy increased in both tasks with phase coherence. A regression analysis revealed a significant linear component to the relationship between phase coherence and both measures of behavior (Table II). These data were subjected to a three‐way within‐subjects ANOVA (stimulus‐category x task x phase‐coherence) revealing significant main effects of task, F(1, 8) = 20.49, P < 0.01, and coherence, F(5, 40) = 236.27, P < 0.001. Post hoc Tukey tests (α = 0.05) revealed significantly higher accuracy for detection than discrimination and significantly higher accuracy for each increasing coherence level except between 60 and 80%. A significant interaction was found between stimulus category × task [F(1, 8) = 9.39, P < 0.05], which were due to differences between detection and discrimination for face, but not place, images.

Figure 4.

Detection and within‐category discrimination for faces and places at different levels of phase coherence. Error bars represent ±1 standard error.

Table II.

Mean R ²‐ and β‐values (and standard errors) of regressions between peak MR amplitude and behavioral accuracy at 20, 40, 60, and 80% phase coherence

		Detection		Categorization
		R 2	β	R 2	β
Face	FFA	0.59 (0.13)**	0.57 (0.20)*	0.72 (0.09)***	0.83 (0.07)***
	PPA	0.33 (0.10)*	−0.23 (0.20)	0.49 (0.11)**	−0.46 (0.19)*
Place	FFA	0.44 (0.09)**	0.39 (0.20)	0.53 (0.09)***	0.51 (0.19)*
	PPA	0.57 (0.06)***	0.75 (0.04)***	0.77 (0.05)***	0.87 (0.03)***

One‐sample t‐tests indicate whether the values differ significantly from zero (above or below).

^* P < 0.05.

^** P < 0.01.

^*** P < 0.001.

To further characterize the relationship between BOLD response and phase coherence, statistical comparisons were made between detection and discrimination accuracy during the independent behavioral experiment, and peak amplitudes during the scaling scans. Regressions were carried out between behavioral accuracy (detection and discrimination tasks) and the peak MR‐amplitude for each stimulus by region pairing. Note that this only included data at 20, 40, 60, and 80% phase coherence. Table III shows the between‐subject mean R ² and β values for each of the fitted regression lines, along with the significance of one‐sample t‐tests comparing the values to zero.

Table III.

Mean R ²‐and β‐values (and standard errors) of regressions between phase coherence and behavioral accuracy

	Detection		Categorization
	R 2	β	R 2	β
Face	0.57 (0.06)***	0.58 (0.17)**	0.77 (0.03)***	0.88 (0.02)***
Place	0.65 (0.03)***	0.81 (0.02)***	0.83 (0.04)***	0.91 (0.02)***

One‐sample t‐tests indicate whether the values differ significantly from zero (above or below).

^** P < 0.01

^*** P < 0.001.

In the FFA, the relationship between the peak MR‐response and discrimination accuracy to faces appears to be more linear [β = 0.83, t(8) = 12.68, P < 0.001; R ² = 0.72, t(8) = 7.92, P < 0.001] than between MR‐response and detection accuracy [β = 0.57, t(7) = 2.86, P < 0.05; R ² = 0.59, t(7) = 4.56, P < 0.01]. Similarly, in the PPA, the relationship between response amplitude and discrimination accuracy [β = 0.87, t(8) = 33.23, P < 0.001; R ² = 0.77, t(8) = 16.97, P < 0.001] appears greater than between MR‐response and detection accuracy [β = 0.75, t(8) = 17.42, P < 0.001; R ² = 0.57, t(8) = 9.38, P < 0.001]. To explicitly test for such an effect the R ² and β‐ value data were subjected to two separate three‐way within‐subjects ANOVAs (Stimulus‐category × Task × Region) revealing a main effect of Task for the R ² data, F(1, 7) = 13.49, P < 0.01 (as well as a trend for the β data, F(1, 7) = 4.13, P = 0.08). This main effect of task was due to greater R ² values for categorization accuracy than detection accuracy, suggesting that the relationship between the peak MR‐response and discrimination accuracy is more tightly correlated than between MR‐response and detection accuracy. We also found a Stimulus × Region interaction for the β data, F(1, 7) = 124.72, P < 0.001 (as well as a trend for the R ², F(1, 7) = 4.97, P = 0.06). This interaction showed that β values were greater for face stimuli in the FFA and place stimuli in the PPA (i.e., preferred stimuli) than for places in the FFA and faces in the PPA. These results mirror the significant three‐way interaction seen between Stimulus‐type, Region, and Coherence‐level suggesting the linearity of the BOLD response is dependent upon both stimulus‐type and region.

Experiment 3: Additivity

To test the principle of additivity, we assessed whether the response to a long block of stimuli could be predicted by summing the responses to shorter blocks. Figures 5 and 6 show the predicted and actual responses in the FFA and PPA to their preferred stimulus category (face and place, respectively). For example, we compared the measured response to an 8 s block of faces with the response that would be predicted from summing four 2 s blocks or two 4 s blocks (Supp. Info. Fig. 2). The graphs show that although the measured responses could generally be predicted by the addition of shorter stimulus blocks, the prediction based on shorter presentations tended to overestimate the measured response from longer presentations. For example, Figure 5 shows that the predicted response in the FFA to faces was consistently larger than the measured response. This was particularly apparent for the addition of 2 s presentations. Similarly, the predicted response in the PPA to places from 2, 4, or 8 s presentations tended to overestimate the measured response, particularly at 8 or 16 s.

Figure 5.

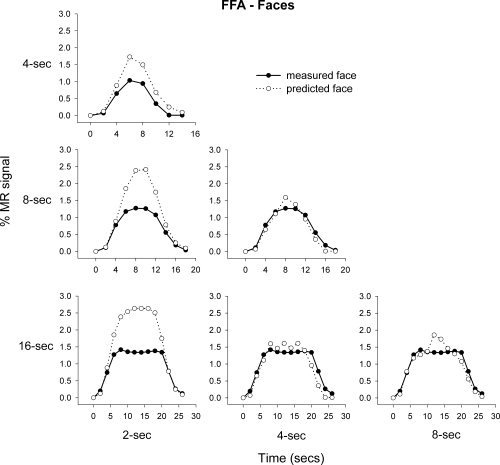
Mean predicted and measured responses to face images in the FFA. The responses to 2, 4, and 8 s blocks were used to predict the measured response at 4, 8, and 16 s.

Figure 6.

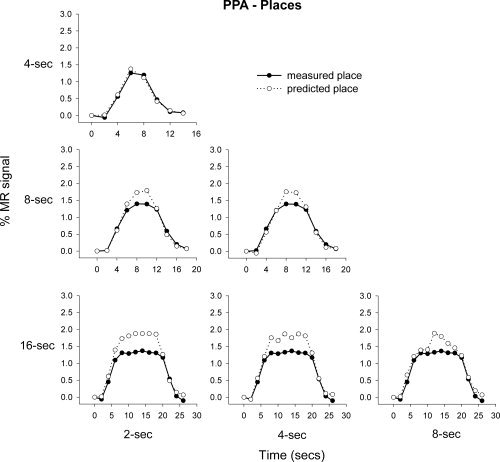
Mean predicted and measured responses to place images in the PPA. The responses to 2, 4, and 8 s blocks were used to predict the measured response at 4, 8, and 16 s.

Regression analyses on the predicted and measured responses in the FFA and PPA to faces and places, respectively were performed on each subject. The mean R ² values across subjects are shown in Table IV; all R ² values are significantly greater than zero (one‐sample t‐test, Bonferroni corrected). Therefore, in the FFA and PPA the predicted 16 s response (predicted from the 2, 4, and 8 s measured responses, respectively) correlated highly with the measured 16 s response. AR‐values between predicted and measured responses in the FFA and PPA to faces and places respectively were performed on each subject. The mean AR‐values across subjects are shown in Table III, showing a significant overprediction of response in the FFA based on the measured 2 s response, and in the PPA based on the 4 s response (one‐sample t‐test, Bonferroni corrected).

Table IV.

Mean R ²‐ and AR‐ (Amplitude Ratio − predicted/measured) values (and standard errors) within the FFA and PPA for preferred and nonpreferred stimuli

	Time (s)	Face		Place
		FFA	PPA	FFA	PPA
R 2‐values	2	0.81 (0.04)*	0.40 (0.09)*	0.21 (0.07)	0.87 (0.04)*
	4	0.78 (0.03)*	0.47 (0.12)	0.26 (0.08)	0.90 (0.01)*
	8	0.79 (0.03)*	0.40 (0.11)	0.17 (0.08)	0.88 (0.03)*
AR‐values	2	1.82 (0.19)*	4.94 (2.4)	1.21 (0.43)	1.29 (0.15)
	4	1.12 (0.10)	0.39 (0.34)	1.47 (0.50)	1.40 (0.07)*
	8	1.17 (0.06)	1.20 (0.40)	1.37 (0.30)	1.32 (0.12)

The responses to 2, 4, and 8 s were used to predict the 16 s response. One sample t‐tests indicate whether: (1) R ²‐values differ significantly from zero; (2) AR‐values differ significantly from 1 (Bonferroni corrected).

^* P < 0.05.

Next, we determined the additivity of the fMRI response in the FFA and PPA to places and faces, respectively. Figure 7 shows that the average predicted and measured responses to places in the FFA appear to be generally consistent with the principle of additivity. However, the mean regression values across subjects reveal that the predicted and measured responses to places in the FFA were more variable across subjects than the corresponding values for faces. For example, the mean regression value between the predicted and measured responses in the FFA to faces was 0.79, whereas the mean regression to places was 0.43 (see Table II). Again, the response predicted from adding shorter stimulus blocks generally overestimated the measured responses at longer time durations, however this overprediction was nonsignificant. Figure 8 shows the response of the PPA to faces. This response was distinctly nonlinear with the predicted and measured responses deviating markedly from each other. Indeed, there was a difference between the amount of measured response variance explained by the predicted response in the PPA to faces (mean R ² = 0.21) and places (mean R ² = 0.88).

Figure 7.

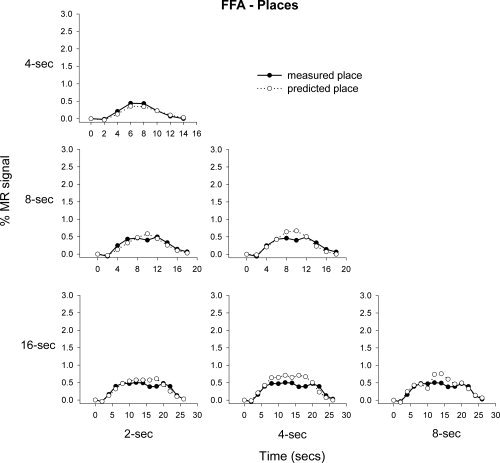
Mean predicted and measured responses to place images in the FFA. The responses to 2, 4, and 8 s blocks were used to predict the measured response at 4, 8, and 16 s.

Figure 8.

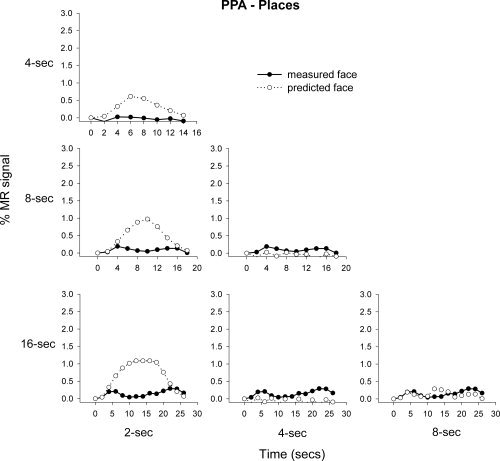
Mean predicted and measured responses to face images in the PPA. The responses to 2, 4, and 8 s blocks were used to predict the measured response at 4, 8, and 16 s.

To explicitly test whether the accuracy of the predicted BOLD response to longer time durations varied as a function of stimulus‐type and region, the regression and AR‐value data were both entered into separate 2 × 2 × 3 (Stimulus‐type × Region × Time‐duration) within‐subject ANOVAs. The regression ANOVA revealed a significant Stimulus‐type × Region interaction, F(1.0, 7.0) = 123.44, P< 0.001. Further post hoc tests revealed significantly greater R ² values for faces than places in the FFA, t(7) = 4.32, P < 0.01, and for places than faces in the PPA, t(7) = 11.10, P <.001 (collapsed across Time‐duration). The AR‐value ANOVA revealed no significant main effects or interactions (F < 4.4, P > 0.08). Therefore, although the correlation between predicted and measured response varied as a function of Stimulus‐type and Region, the overprediction in amplitude was consistent across Stimulus‐type, Region, and Time‐scale.

Behavioral accuracy during face and place additivity scans (within‐category stimulus detection) remained high (μ = 97%, σ = 0.04). Accuracy was not significantly affected, by either block length or target category respectively, in face, F(1.7, 10.2) = 0.45, P > 0.05, F(1, 6) < 0.01, P > 0.05, and place, F(1.9, 11.4) = 1.02, P > 0.05, F(1, 6) = 2.97, P > 0.05, scans. Reaction times were equally unaffected by block length and target category in face, F(3, 18) = 1.50, P > 0.05, F(1, 6) = 0.13, P > 0.05, and place, F(3, 18) = 0.98, P > 0.05, F(1, 6) = 1.69, P > 0.05, scans.

DISCUSSION

The aim of this study was to investigate the linearity of the BOLD response to complex objects in the inferior temporal cortex. Specifically, the properties of scaling and additivity were assessed in face‐selective and place‐selective regions for face and place stimuli. Results showed an approximately linear response for preferred stimuli in both the FFA and PPA. In contrast, the response to nonpreferred stimuli demonstrated a greater divergence from linearity. Therefore, the pattern of nonlinearities varied as a function of both cortical region and stimulus category.

The relationship between neural activity and the BOLD response is often described as being linear [Friston et al., 1995]. However, to be linear, a system must conform to certain properties, such as scaling and additivity. We assessed the property of scaling in category selective regions of the human ventral visual pathway by varying the phase coherence variation of complex objects (faces and places). For scaling to hold, the MR response amplitude should demonstrate proportional increases with phase coherence. We found that the BOLD response in the FFA and PPA was roughly commensurate with changes in the phase coherence of the preferred stimulus. Furthermore, the BOLD response to the preferred stimulus correlated well with behavioral judgements on the detection and discrimination of the stimulus. For example, significant correlations were apparent between behavioral performance to faces and places and the peak response to these stimuli in the FFA and PPA, respectively. Category discrimination was more tightly correlated to response amplitude than detection accuracy.

The linearity of the BOLD response that we report contrasts with the findings from previous studies that have found nonlinear responses in the ventral visual pathway. For example, Avidan et al. [2002] found that the response in category‐selective regions of visual cortex did not vary linearly with the contrast of face and object images. Similarly, Mukamel et al. [2004] failed to find a linear relationship between stimulus presentation rate and the BOLD response in ventral stream regions. However, in both studies a linear response was evident in early visual areas. One explanation for this discrepancy could be the paradigms used to vary stimulus strength may not have had a corresponding effect on the neural activity in the ventral stream visual areas. For example, significant changes, in contrast, have minimal effects on object recognition [Avidan et al., 2002]. Similarly, increasing rate of presentation can decrease the ability to discriminate and process complex objects [Grill‐Spector et al., 2000; McKeeff et al., 2007], perhaps as a result of backward masking [Keysers et al., 2001; Kovacs et al., 1995]. Thus, it is possible that the stimulus manipulations used in previous studies may not have increased the underlying neural activity in these ventral stream regions.

Additivity in a linear system is related to the integration of individual responses over time. Thus, the output of a system to more than one input is equal to the sum of the responses to the individual inputs had they occurred in isolation. In this study, we investigated whether the addition of shorter duration responses predicted the response to longer duration stimulus presentations. BOLD responses to preferred stimuli in the FFA and PPA were found to roughly conform to the principle of additivity. However, summation of the responses to shorter duration stimuli often overestimated the response at longer durations. Overprediction of response amplitude for face images at short block durations is in line with previous research both in object‐selective [Kushnir et al., 1999], and early [Boynton et al., 1996; Vazquez and Noll, 1998], visual cortex. For example, Boynton et al. [1996] also found that in V1 the predicted response from adding the response to many short duration (3 s) stimuli was greater than that which was measured to a longer duration stimulus.

One possible explanation for the nonlinear addition of short duration stimuli could be neural adaptation, whereby a decreased neural response is associated with repeated or sustained presentation of a stimulus. For example, the BOLD response to the continued presentation of an object shows an initial peak or transient response followed by a more sustained response in object‐selective regions of the ventral visual stream [Gilaie‐Dotan and Malach, 2008]. Indeed, the significant overprediction found for 2 s presentation of faces in the PPA is consistent with the former study's results, which showed a rapid attenuation of response in the PPA with the response to face stimuli returning to baseline levels despite the continued presence of a face stimulus. Consistent with Boynton et al. [1996], a number of studies have reported that at short intervals (<5 s) the BOLD response to a visual stimulus was reduced in amplitude relative to that predicted by adding two isolated events [Dale and Buckner, 1997; Huettel and McCarthy, 2000; Miller et al., 2001; Pfeuffer et al., 2003]. However, if a longer interval was present between consecutive stimuli, the BOLD response was predicted by the linear addition of the individual responses. These refractory effects seem to be stimulus specific with a greater nonlinearity occurring when an identical stimulus is repeated [Boynton and Finney, 2003; Huettel et al., 2004; Soon et al., 2003].

The overestimation of the BOLD response at longer stimulus durations could also be explained by a nonlinear saturation of the BOLD response, in which increases in neural activity beyond a particular threshold do not result in any additional haemodynamic signal. Consequently, the predicted BOLD signal from a shorter stimulus block would overestimate the response to a longer stimulus block, if the neural response to the longer block exceeds this threshold. Moreover, the difference in response between the predicted and measured response should increase with stimulus duration. This could provide an explanation for the response to place images in the PPA (see Fig. 6). However, it cannot explain the data in the FFA, where the predicted response from a 2 s stimulus block is greater than the measured response from a 4 s block, despite the fact that the response at 4 s is below the maximal response in this region (see Fig. 5). So, while this does not rule out the possibility that saturation of the BOLD response, it does not appear to be the only explanation.

In contrast to the BOLD response to the preferred stimulus, the response to the nonpreferred stimulus was distinctly nonlinear. For example, there was only a slight increase in MR‐response in the FFA to places with increased phase coherence, whereas the response to faces in the PPA actually decreased with the increased visibility of the stimulus. Similar nonlinearities were apparent when shorter duration stimulus blocks were used to predict the response of longer duration blocks. This was particularly apparent in the response of the PPA to images of faces, where there was a marked difference between the predicted and measured responses. One possible explanation of this interesting finding is that it indicates a rapid suppression of activity for the nonpreferred stimulus. Indeed, the difference in the BOLD response to preferred and nonpreferred stimuli shown in this study suggests that the measured nonlinearities were present at the neural level. This is because, although nonlinearities between neural activation and the BOLD response could vary as a function of cortical region, they are less likely to vary as a function of stimulus type.

Measures of linearity could provide a useful measure of stimulus selectivity in the visual system. Selectivity in neuroimaging studies is typically determined by comparing the relative response to different types of visual stimulus. However, the greatest response to a stimulus need not imply that this neural population is only selective for that particular stimulus. Because of the spatial limitations of functional imaging, the measured signal is determined by the summed activity of many thousands of neurons. Regions defined as “face‐selective” could either contain a homogeneous population of face‐selective neurons or a heterogeneous population of neurons with the majority being selective for face images [Andrews, 2005]. It is conceivable, therefore, that the linearity of the BOLD response to a stimulus could be unrelated to the selectivity for that stimulus. We would also predict that, while voxels in early visual areas would show a significant response to these complex visual stimuli, they would not show a linear response to changes in phase coherence. This analysis could, therefore, distinguish between brain regions involved in processing low‐level and high‐level representations of a stimulus. Indeed, such an approach may have advantages compared to more conventional functional localization techniques which typically compare activation for a stimulus category of interest (e.g., faces) compared to that of another stimulus category (e.g., houses, objects, or scrambled images), in that it does not suffer from the same problems of appropriate comparator selection.

The present results show that the BOLD response in category selective regions of the human visual system was generally linear to the preferred stimulus. This conclusion adds to previous research demonstrating a roughly linear response in primary visual cortex [Boynton et al., 1996; Miezen et al., 2000; Vazquez and Noll, 1998; see also Logothetis et al., 2001 for evidence of linearity in macaque early visual cortex], and primary auditory and motor cortex [Soltysik et al., 2004]. However, we also extend these findings by reporting that a more nonlinear response was apparent to the nonpreferred stimulus. The difference in the fMRI response to preferred and nonpreferred stimuli shown in this study suggests that measures of linearity may provide a useful indication of neural selectivity in the visual system.

Supporting information

Additional Supporting Information may be found in the online version of this article.

Supporting Information Figure 1. Counterbalancing design used to present stimulus conditions in the scaling and additivity scans.

Supporting Information Figure 2. Mean measured responses to stimulus blocks containing faces or places at different stimulus durations across all subjects. Error bars represent ±1 standard error.