Abstract
Population maps of the corpus callosum (CC) and cortical lobe connections were generated by combining cortical gray matter parcellation with the diffusion tensor fiber tractography of individual subjects. This method is based on the fact that the cortical lobes of both hemispheres are interconnected by the corpus callosal fibers. T1‐weighted structural MRIs and diffusion tensor MRIs (DT‐MRI) of 22 right‐handed, healthy subjects were used. Forty‐seven cortical parcellations in the dorsal prefrontal cortex, ventral prefrontal cortex, sensory‐motor cortex, parietal cortex, temporal cortex, and occipital cortex were semi‐automatically derived from structural MRIs, registered to DT‐MRI, and used to identify callosal fibers. The probabilistic connections to each cortex were mapped on entire mid‐sagittal CC voxels that had anatomical homology between subjects as determined by spatial registration. According to the population maps of the callosal connections, the ventral prefrontal cortex and parts of the dorsal prefrontal cortex both project fibers through the genu and rostrum. The CC regions through which the superior frontal cortex passes extend into the posterior body. Fibers arising from the parietal lobe and occipital lobe run mainly through the splenium, while fibers arising from the sensory‐motor cortex pass through the isthmus. In general, dorsal or medial cortical lobes project fibers through the dorsal region of the CC, while lateral cortical lobes project fibers through the ventral region of the CC. The probabilistic subdivision of the CC by connecting cortical gray matter provides a more precise understanding of the CC. Hum Brain Mapp 2008. © 2006 Wiley‐Liss, Inc.
Keywords: diffusion tensor, corpus callosum, tractography, cortical parcellation
INTRODUCTION
Corpus callosal fibers interconnect the cerebral hemispheres. The critical role of these fibers is in functional associations between the two hemispheres and has long been an area of research interest. The traditional approach has been to measure the area of either the whole corpus callosum (CC) or a subdivision of the mid‐sagittal section to evaluate their role in functional, behavioral, and/or gender differences. This volumetric approach is based on the hypothesis that the size of the mid‐sagittal area of the CC is related to the total number of fibers and, therefore, is an indicator of neural connectivity between the hemispheres [Aboitiz et al., 1992].
The CC is not a homogenous structure. Instead, the CC appears to topographically represent the various cortical lobes that are associated with the functional specialization of callosal subdivisions. The CC is often subdivided into the genu, midbody, isthmus, and splenium (see Fig. 1A). However, the CC does not have characteristic landmarks reflecting the neuronal fiber properties, which are used as a basis for subdivision. Therefore, the various methods for defining the CC partitioning have been based on mid‐sagittal geometry. Widely applied methods of mid‐sagittal CC partitioning have included the use of vertical lines spaced at fractions on the maximal anterior–posterior length [Duara et al., 1991; Witelson 1989] (see Fig. 1A) or the use of equal angular sectors relative to the callosal centroid [Clarke et al., 1989]. Other proposed methods for detailed shape analysis include a boundary model‐based subdivision using equally matched upper and lower boundaries [Denenberg et al., 1991] and a medial model‐based subdivision using equal divisions along the medial line of the CC [Peters et al., 2002]. The use of various partitioning methods may contribute to the discrepancies between study results on gender, handedness, and schizophrenia in relation to the CC area [Bishop and Wahlsten, 1997]. Notably, each partitioning method described earlier is basically geometric and does not take into account neuronal fiber composition or fiber connections through the CC.
Figure 1.
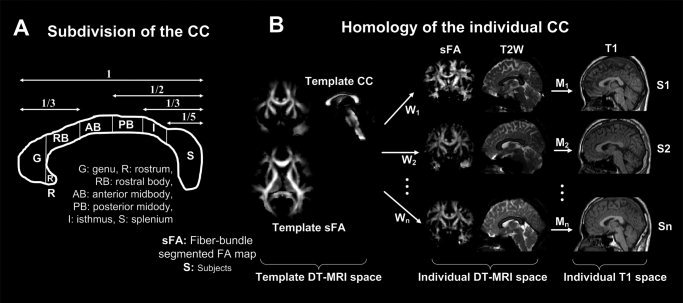
Regional geometric subdivision of the CC and procedures for matching the anatomical homology of the CC. A widely used subdivision of the CC suggested by Witelson [1989] is displayed in the left panel (A). This geometric subdivision is based on neither fiber composition nor fiber connection through the CC. The right panel (B) shows the spatial normalization process that was used. The voxel‐wise anatomical homology between each subject's CC was found by mapping each CC to a template CC by applying nonlinear warping W between a fiber‐bundle segmented fractional anisotropy map and individual segmented fractional anisotropy maps. Statistical evaluation was performed on this anatomical homology of the CC. The correspondence between the DT‐MRI and T1‐weighted image of a subject was found by affine transformation (M) of the T2‐weighted b0‐image (T2W) of DT‐MRI to the T1‐weighted image (T1) of the subject.
An in vitro approach has been used to subdivide the CC according to fiber composition or fiber connections. The CC axonal fiber composition was explored by Aboitiz et al. [1992] in 20 postmortem human brains. This group found that the density of thin fibers (smaller than 2 μm in diameter) peaks at the genu. These fibers decrease toward the posterior midbody and increase in the posterior pole of the CC. In contrast, the opposite is true for thick fibers. This topographic distribution of heterogeneous fibers supports the rationale for studying the subdivided CC and could be used to subdivide the CC.
The relationship of callosal fibers to the division of the cerebral cortex has been researched in cats [Lomber et al., 1994], in the posterior parietal and superior temporal cortical and the inferior premotor regions of rhesus monkeys [Cipolloni and Pandya, 1985; Pandya et al., 1971; Seltzer and Pandya, 1983], and in the temporal lobe regions of macaques [Demeter et al., 1990]. These studies were all accomplished using an autoradiographic tracing method. As noted by de Lacoste et al. [1985], sulcal and gyral configurations of cat, rhesus, and macaque brains differ conspicuously from the human brain. The association lobes of these animals are poorly developed, which might make their CC topography incompatible with the human brain.
In humans, the CC fiber topological distribution was determined by correlating the Wallerian degeneration distribution in the CC with anatomical sites of focal cortical lesions [de Lacoste et al., 1985]. This in vitro method of CC partitioning by fiber connectivity is potentially vulnerable to shrinkage, deformation, and damage during postmortem fixation. Furthermore, the number of samples in this study was too limited to allow for statistical evaluation of the possible intra‐group variations in the whole brain fiber connections.
In vivo examination of the CC tissue properties and fiber connectivity can be conducted using diffusion tensor magnetic resonance imaging (DT‐MRI). The CC fiber properties have been assessed by using diffusion indices such as fractional anisotropy (FA) and mean apparent diffusion coefficients [Moeller et al., 2005; Shin et al., 2005]. DT‐MRI also shows the local fiber orientation through the major eigenvectors of the diffusion tensor at each voxel. Thus, it is possible to use this local orientation information iteratively across many voxels to propagate a virtual particle and thereby trace the fiber to the outer white matter [Basser et al., 2000; Conturo et al., 1999; Jones et al., 1999; Mori et al., 1999]. Fiber tractography, a method of estimating fiber streams by connecting points along the anisotropic diffusion direction, has been used to identify callosal fiber distributions [Tench et al., 2002]. Xu et al. [2002] showed a framework for the population distribution of fibers that crossed several positions in the CC. In addition, Abe et al. [2004] presented callosal fibers crossing the genu and splenium using tractography. Both methods used fiber tractography seeding from predefined regions of the CC. Recently, Huang et al. [2005] applied DT‐MRI tractography in parcellating the CC. In this study, the CC was divided into six major subdivisions using a 2‐regions of interest (ROI) method of fiber tractography for eight subjects (five right‐handed and three left‐handed). Six ROI planes were defined in a relatively coarse and arbitrary way, and fibers crossing the CC were partitioned according to the secondary planes that they crossed. However, this method of CC parcellating using fiber tractography is not based on precise cortical gray matter structures and therefore has a limited ability to cluster fibers according to the detailed partitions of the cortical structures that they connect. Dougherty et al. [2005] presented occipital‐callosal projections from four subjects using diffusion tensor imaging seeded from the manually defined occipital lobe. The results were related to four cortical visual field maps derived from functional MRI (fMRI). This study is important because it was the first to match anatomical connectivity with functionally defined maps. Unfortunately, these results were restricted to four occipital subregions and a small subject number (N = 4).
Thus far, no study has shown population topographic maps of the CC by individual cortical gray matter parcellation covering the entire brain. Therefore, in this article, we present CC population connectivity maps in 22 normal, healthy subjects by combining DT‐MRI with cortical gray matter subdivisions. These subdivisions were semi‐automatically partitioned into approximately 47 cortical subregions in the dorsal–prefrontal, ventral–frontal, sensory‐motor, parietal, temporal, and occipital cortexes.
METHODS
Subjects
Twenty‐two healthy volunteers (11 males and 11 females) were recruited from the community and were screened for a current or lifetime history of any DSM‐IV Axis I disorder using the SCID [First et al., 1996]. All subjects were right‐handed, with a mean age of 30.3 years (SD = 3.1, range = 25–35). None had a history of traumatic brain injury, epilepsy, alcohol/substance abuse, or neurological problems. Written informed consent was obtained from the subjects after the study was described in detail. The study was conducted under the guidelines for the use of human subjects that were established by the institutional review board.
Image Acquisition and Preprocessing
DT‐MRI data were acquired at the Severance Hospital using a Philips 1.5T scanner (Philips Intera, Philips Medical System, Best, The Netherlands) with a SENSE head coil. Head motion was minimized with restraining foam pads provided by the manufacturer.
A high‐resolution T1‐weighted MRI volume data set was obtained axially with the following acquisition parameters: 224 × 224 acquisition and 256 × 256 reconstructed matrix, 240 mm field of view, 0.9375 × 0.9375 × 1.5 mm3 voxels, TE 4.6 ms, TR 20 ms, flip angle 25°, slice gap 0 mm, 1 averaging per slice, noncardiac gating, resampled into 256 × 256 matrix, (1 × 1 × 1 mm3), and 256 axial slices. Diffusion‐encoded images, parallel to the anterior commissure–posterior commissure line, were obtained using a single‐shot echo‐planar acquisition with the following parameters: 112 × 112 acquisition and 128 × 128 reconstructed matrix, 220 mm field of view, 1.72 × 1.72 × 2 mm3 voxels, approximately 55 axial slices, SENSE factor 2, TE 70 ms, TR shortest (about 13,000 ms), flip angle 90°, slice gap 0 mm, b‐factor of 600 s/mm2, noncardiac gating. Diffusion‐weighted images were acquired from 32 noncollinear, noncoplanar directions provided by Philips with a baseline image containing minimum diffusion weighting, also called a b0‐image.
The spatial distortions induced by eddy currents in the diffusion‐weighted images were corrected using an AIR5 algorithm [Woods et al., 1992]. This algorithm registered the diffusion‐weighted images to the b0‐image. We also used second order nonlinear registration, which performed better in eddy current correction than the affine linear registration [Kim et al., 2005].
DATA PROCESSING
CC Template Generation
To minimize errors in spatial registration used in anatomically matching the CC between subjects, a group average template of diffusion tensor images was created using the method described in the paper [Park et al., 2003].
In brief, the diffusion tensor template was constructed using an iterative spatial normalization scheme combining the mean intensities of the spatially registered diffusion tensor images and the mean deformation fields from individual diffusion tensor images [Guimond et al., 2000]. A diffusion tensor image from the group was chosen as a temporary template, and all other diffusion tensor images were registered to this temporary template. The average of the registered tensor images was resampled with the inverse of the average deformation field to achieve the morphological (shape) mean as well as the mean intensity. The resampled average diffusion tensor image was used again for the target template of the next iteration. Four iterations were used to create an average brain diffusion tensor template. During the registration, the tensor orientations were adjusted iteratively according to deformation field using the preservation of principal direction algorithm, as described by Alexander et al. [2001].
A template CC was manually delineated at the mid‐sagittal slice in the segmented FA map of the final average diffusion tensor template.
Mapping From a Template CC to Individual DT‐MRI Spaces
Mapping from a template CC to individual DT‐MRI spaces was a two‐step process: (1) generation of a segmented FA map of the diffusion tensor template along with segmented FA maps of individual diffusion tensor images, and (2) nonlinear transformation of the segmented FA map of the template to segmented FA maps of individual tensor images (W in Fig. 1B).
Segmented FA maps of both individual tensor images and the tensor template were generated by using fiber tractography with seed points at the whole brain white matter as described in the following section. The streamline points of each fiber bundle have FA of the tensor defined by Basser and Pierpaoli [1996] in the continuous tensor field. The mean FA at a voxel was calculated by averaging FA at the corresponding streamline point of all fiber bundles that passed the voxel. Since the mean FA was defined only where the fiber‐bundles passed, the generated FA map appeared to be segmented by the fiber bundles.
Nonlinear transformation from the template to individual images was calculated using the Demon's algorithm [Guimond et al., 2001], which derives deformation fields from the template segmented FA map to the segmented FA maps of individual brains. Using the calculated nonlinear transformations, the CC points from individuals homologous to the template CC points were found by transforming the points in the template CC into individual DT‐MRI space. Since the segmented FA map represents where fiber bundles were reconstructed, the registration algorithm appeared to match homologous positions at mid‐sagittal CC voxels more reliably than the registration of T2‐weighted images.
To classify the fiber bundles according to their connection to cortical parcellations in the T1‐weighted images, the individual T2‐weighted B0 diffusion weighted images acquired as the baseline of DT‐MRI were co‐registered to the T1‐weighted image using an affine transformation of the SPM2 co‐registration algorithm [Ashburner and Friston, 1997].
Corpus Callosal Fiber Extraction
Automated fiber tracking and processing of the diffusion tensor images was accomplished using DoDTI (Yonsei University, http://neuroimage.yonsei.ac.kr/dodti), home‐made software, which runs on MATLAB6 [Mathworks, USA]. The fourth order Runge‐Kutta method was used as the integration solver [Press et al., 1992] in fiber tracking. This fiber tracking algorithm virtually creates a trace of propagating streamlined points by following the local fiber orientation, which is defined by the diffusion tensor field.
Instead of tracking fiber bundles starting from a seed point, whole white matter fiber bundles were reconstructed and fiber bundles crossing the given seed point were extracted. This approach effectively reduces problems caused by the partial volume effect in the diffusion tensor image [Mori and Van Zijl, 2002]. For the reconstruction of whole white matter fiber bundles, seed points were assigned at all voxels inside the white matter segmented using SPM2 [Ashburner and Friston, 1997]. The seed point number was approximately 80,000; therefore, a corresponding number of fiber tracks were constructed. The stopping criteria for fiber tracking included a low FA (0.2) and a rapid change of direction (60° per 1 mm). A trilinear interpolation method was used for obtaining the subvoxel estimation with a 1‐mm step size.
Callosal fibers were chosen from the reconstructed fibers, which crossed the CC points of each subject, corresponding to the template CC points.
Clustering of Corpus Callosal Fibers Using Gray Matter Parcellation
The extracted callosal fibers were automatically labeled using cortical gray matter parcellation derived from the T1 images. Cortical gray matter from the structural T1 images was partitioned using FreeSurfer (MGH, Harvard Medical School), a program that parcellates the cortex into 84 anatomically relevant brain subregions using a surface‐based approach [Fischl et al., 2004]. From 84 subregions, only 64 cortical gray matter regions were selected by removing the white matter subregions and merging the small and over‐fractionized subregions.
The coordinates from the streamlined points of the corpus callosal fibers were transformed into T1‐image space using the affine transformation. This transformation was previously derived from matching the DT‐MRI T2‐weighted image to the T1 image (M in Fig. 1B). All fibers were classified by assigning the fibers labels of the cortical parcellations where each fiber ended [Park et al., 2004a]. To make a fiber streamline fall into or hit the gray matter cortical layer, we extended the streamline propagation to two more steps (2 mm) along the propagation direction at the terminal point of the streamline. The five successive end points (5 mm in total length) from the terminal point on each side of the fiber streamline were hit‐tested with every cortical parcellation. The index of cortical parcellations maximally hit by these five end points was assigned to each fiber side representing a cortical connection through the fiber.
Figure 2 shows the clustering of corpus callosal fibers from a subject using cortical gray matter parcellation. Figure 2A displays half of the callosal fibers bisected by a mid‐sagittal plane, indicating where the topographic mapping was conducted. The gradual colors assigned to the callosal fibers in Figure 2A were based on the similarity between fibers. The similarity between fiber endpoints was determined using the method by Brun et al. [2004] without any reference to the connection of the cortical gray matter parcellation displayed in Figure 2B. In contrast, Figure 2C shows the callosal fiber interconnection using a parcellated CC color‐coded with cortical gray matter parcellation labels.
Figure 2.
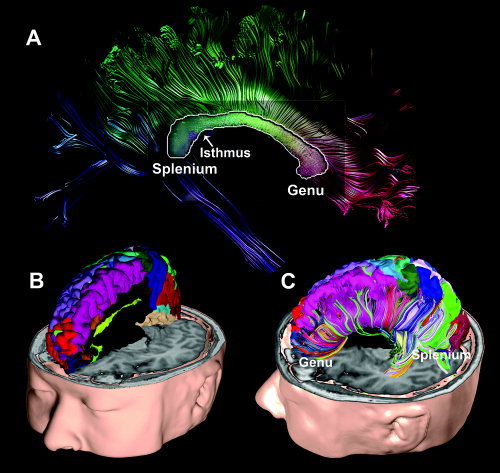
Callosal fiber parcellation of a subject using cortical gray matter parcellation. Approximately 64 gray matter parcellations from the structural T1 image were used to parcellate the white matter fiber bundles. Panel A shows a cross‐section of callosal fibers in the mid‐sagittal plane. The cross‐section is displayed with continuous colors irrelevant to the cortical gray matter parcellation. The callosal fiber colors in panel A were assigned by their similarity to neighboring fibers, i.e., similar directional fibers have similar colors. Panel B shows cortical parcellation that was used to parcellate callosal fibers according to their connection to the cortical lobes. Panel C shows the parcellated callosal fibers color‐coded according to the assigned colors of their interconnecting cortical lobes.
Probabilistic CC Topography
Because of the low DT‐MRI spatial resolution (about 2 × 2 × 2 mm3), several tissue structures may lie within a specific voxel and contribute to the formation of a single tensor at that particular voxel. Therefore, instead of assigning a dominantly connected cortical parcellation index to a CC voxel, each cortex has a probabilistic connection map to all CC voxels. In this way, a voxel could represent multiple fiber bundles that connect different cortical lobes.
For each subject's cortex, a probabilistic CC connection map was created using the parcellated fibers that were derived as described earlier. The connection probability at each CC voxel to a specific cortical region was defined as the ratio of the number of callosal fibers interconnecting a given cortical region versus the number of callosal fibers interconnecting all cortical regions through the voxel (total number of cortical subregions, C = 64). This is summarized by the equation below:
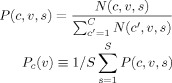 |
(1) |
where N(c, v, s) is the number of fibers connecting the cortex subregion (c) through voxel (v) for a subject (s) in the group sample size (S = 22). The population callosal map of a cortical subregion c, i.e., Pc(ν), was derived by averaging individual probabilistic CC connection maps (P(c, v, s)) for the cortical lobe c. In counting N(c, v, s), if a fiber connected two cortical regions of both hemispheres, including either a homotopic or a heterotopic cortical region at the contralateral hemisphere, we assigned two cortical indices (c) for a voxel (v). If a fiber connected a cortical region and a noncortical structure, a cortical index (c) was assigned to the voxel (v) when defining N(c, v, s).
The definition in Eq. (1) does not take into account the varying numbers of connections of a cortical region likely to be identified for each voxel. To know if more or less connection to given cortical regions are identified in one voxel relative to another, an additional connection probability was defined by the equation below:
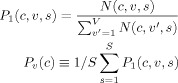 |
(2) |
where V is the total number of voxels in the CC. Connection probabilities defined in Eqs. (1) and (2) between a voxel and a cortical region differ in the normalization term: in Pc(v), the number of interconnecting fibers normalized by the total callosal fibers crossing a voxel v; and in Pv(c), the number of interconnecting fibers normalized by the total fibers crossing a cortical region c.
We used the probabilistic population connection maps of the CC cortical subregions defined by Eq. (1) to generate the first and second most dominant connection maps. To accomplish this, color labels representing the cortical subregions with the first or second maximal callosal connection probabilities were assigned to each voxel.
The reliability of the most dominant connection map was evaluated by calculating the voxel‐by‐voxel correspondence between a dominant connection map of an individual subject and the group of 22 subjects. The voxel‐by‐voxel correspondence rate was defined using the following equation:
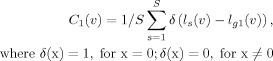 |
(3) |
where C 1(v) is the correspondence rate at the voxel v for the total subject number (S = 22), and ls(v) and l g1(v) are the most dominant cortical labels at the voxel v for subject s and for the group of 22 subjects.
The rate at which an individual CC voxel mediates the connection of the cortical subregion to either the first or second most dominant group maps was defined by the additional correspondence rate:
| (4) |
where C 2(v) is the correspondence rate at the voxel v between cortical label (ls(v)) of the most dominant connection map of a subject s and those of the first (l g1(v)) and the second (l g2(v)) most dominant connection map.
RESULTS
The population callosal maps defined by Eq. (1) are presented in the following categories: dorsal prefrontal cortex and ventral prefrontal cortex (Fig. 3A), sensory‐motor cortex and parietal cortex with cingulate (Fig. 3B), temporal cortex and occipital cortex (Fig. 3C). Cortical parcellations of the average cortical surface in the subjects (N = 22) are displayed as 3D rendered cortical surfaces to specify the cortical regions corresponding to the callosal maps. The upper left color bar in each callosal map shows the color of the corresponding cortex subregion on a 3D surface. The right color bar shows the probability scale with the maximal range given in percentage units. Out of the approximately 64 cortical subregions parcellated from the whole cortical gray matter, we have displayed 47 cortical subregion connection maps, which contain a certain number of callosal interconnections.
Figure 3.
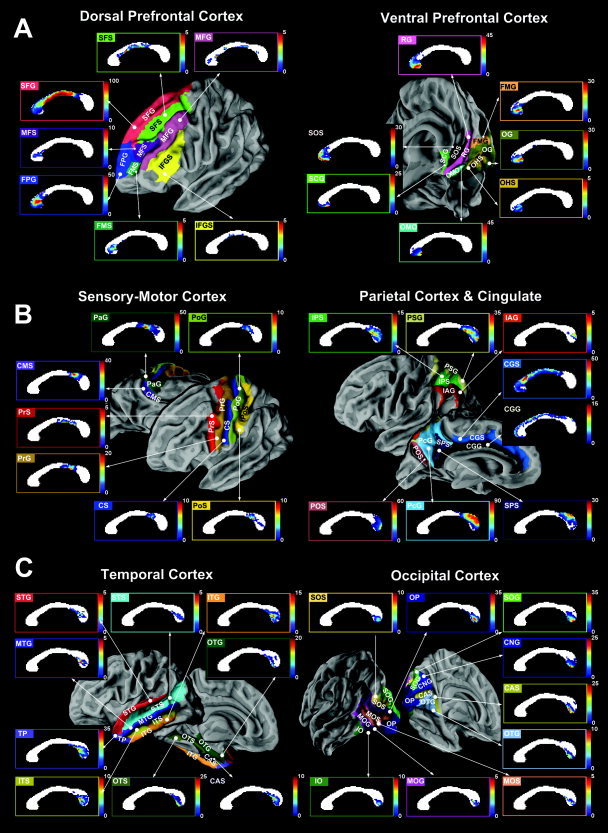
Statistical callosal connection maps of the cortex. A: Callosal connection maps of the interhemispheric dorsal prefrontal cortex were derived from the superior frontal gyrus (SFG), transverse frontopolar gyrus (FPG), superior frontal sulcus (SFS), middle frontal sulcus (MFS), frontomarginal sulcus (FMS), middle frontal gyrus (MFG), and inferior frontal gyrus and sulcus (IFGS). Callosal connection maps were also derived from the ventral prefrontal cortex, including the rectus gyrus (RG), orbital medial/olfactory sulcus (OMO), orbital gyrus (OG), suborbital sulcus (SOS), frontomarginal gyrus (FMG), subcallosal gyrus (SCG), and orbital H‐shaped sulcus (OHS). The color scale indicates the percentage of interconnection to a given cortical region when compared with other cortical regions at each voxel. B: Callosal connection maps of the interhemispheric sensory‐motor cortex were derived from the cingulated sulcus marginalis region (CMS), paracentral gyrus (PaG), precentral gyrus (PrG), precentral sulcus (PrS), central sulcus (CS), postcentral sulcus (PoS), and postcentral gyrus (PoG). Callosal connection maps were also derived from the parietal cortex, including the precuneus gyrus (PcG), parieto‐occipital sulcus (POS), subparietal sulcus (SPS), parietal superior gyrus (PSG), intraparietal and parietal transverse sulcus (IPS), and parietal inferior gyrus angular part (IAG). Connection maps of cingulated gyrus (CGG) and cingulate sulcus (CGS) are also shown. C: Callosal connection maps of the interhemispheric temporal cortex were derived from the temporal pole (TP), occipito‐temporal medial and lingual sulcus (OTS), occipito‐temporal medial gyrus parahippocampal region (OTG), collateral transverse anterior sulcus (CAS), inferior temporal gyrus (ITG), inferior temporal sulcus (ITS), superior temporal gyrus (STG), superior temporal sulcus (STS), and middle temporal gyrus (MTG). Callosal connection maps were also derived from the occipital cortex, including the occipital pole (OP), occipital superior gyrus (SOG), calcarine sulcus (CAS), cuneus gyrus (CNG), occipito‐temporal medial gyrus lingual part (OTG), occipital superior and transversalis sulcus (SOS), occipital inferior gyrus and sulcus (IO), occipital middle and Lunatus sulcus (MOS), and occipital middle gyrus (MOG).
The CC is predominantly made up of fibers interconnecting the prefrontal cortex, a region which extends from the genu to the posterior part of the midbody. Cortical regions in the sensory‐motor cortex are interconnected mainly through the isthmus. Fibers from the parietal lobes cross dorsal areas of the splenium and isthmus, while fibers from the occipital lobes pass through the ventral region of the splenium. Fibers connecting the temporal lobes run mainly in a posterior–anterior direction, largely connecting via the posterior and ventral CC regions, such as the splenium or posterior isthmus. Throughout the cortical lobes, the medial‐sided cortical lobes (e.g., CMS, PcG, SPS, CGS, CGG in Fig. 3B) tend to interconnect through the relatively dorsal CC region. While in contrast, the lateral‐sided cortical lobes (e.g., SFS, MFG, IFGS in Fig. 3A and PrS and PrG in Fig. 3B) tend to interconnect through the relatively ventral CC region.
Figure 4 displays the first and second most dominant cortical connection maps of the CC. The color of each CC voxel represents the color of the cortical subregion (Fig. 4A) that interconnects both hemispheres through the voxel with the first (Fig. 4B) and second (Fig. 4C) maximal probability. Figure 4A shows only the cortical subregions that were depicted in Figure 4B,C. These regions have at least one CC voxel through which the cortical lobe is the first or second most dominantly interconnected when compared with other cortical regions. Most of the CC regions are prominently expressed with medial cortical connections. Compared to the most commonly used geometric subdivisions generated by Witelson [1989], which are shown as white vertical lines, cortical connection maps using this method provide a more detailed subdivision of the CC.
Figure 4.
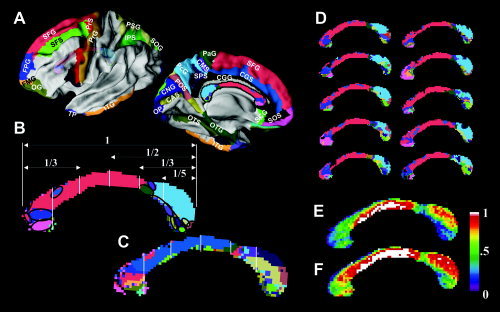
Dominant connection maps of the CC. The most dominant connection map of the corpus callosum (B) shows the color label distribution of the corresponding cortical lobes (A) that have the maximal interconnection probability through each voxel from all of the cortical subregions. Panel C shows the second most dominant map with cortical lobes that have the second most probable interconnection through each voxel. In panel B, a geometric subdivision method using vertical lines suggested by Witelson [1989] is overlaid with the callosal connection map derived from DT‐MRI. Ten examples of the most dominant individual subject maps are displayed in panel D. Panel E shows the correspondence rate between the 22 individual, most dominant maps and the most dominant map of the group (B). Panel F shows the correspondence rate between 22 individual, most dominant maps and either the most dominant map (B) or the second most dominant map (C).
By visual analysis, we found a relatively consistent distribution of dominant cortical labels across the subjects. This is demonstrated in Figure 4D, which displays examples of the individual, most dominant connection maps from 10 randomly chosen subjects. The reliability of the most dominant connection map (Fig. 4B), when applied to an individual CC, can be examined in Figure 4E,F. These figures show the reliability that a voxel of the mid‐sagittal CC belongs to the most dominant cortical label (Fig. 4E), and either the first or the second most dominant cortical labels (Fig. 4F). The reliability of the dominant CC connection maps is high at the body and dorsal splenium where fibers predominantly interconnect the superior frontal cortex and parietal cortex. In contrast, the reliability of this connection map is low at the ventral splenium where fibers mainly connected the temporal cortex. These correspondence rate maps are thought to represent the inter‐individual variability of fiber connections; however, we cannot disregard the effects of errors in the acquisition and processing of the DT‐MRI. Such errors would include acquisition noise, registration errors, and fiber tracking.
Probabilistic connection maps defined by Eq. (2) are displayed in Figure 5, which shows the topographic projection from the cortical lobes through the CC. The topographic pattern of probabilistic connection maps in Figure 5 was found to be similar to the pattern of connection maps displayed in Figure 3.
Figure 5.
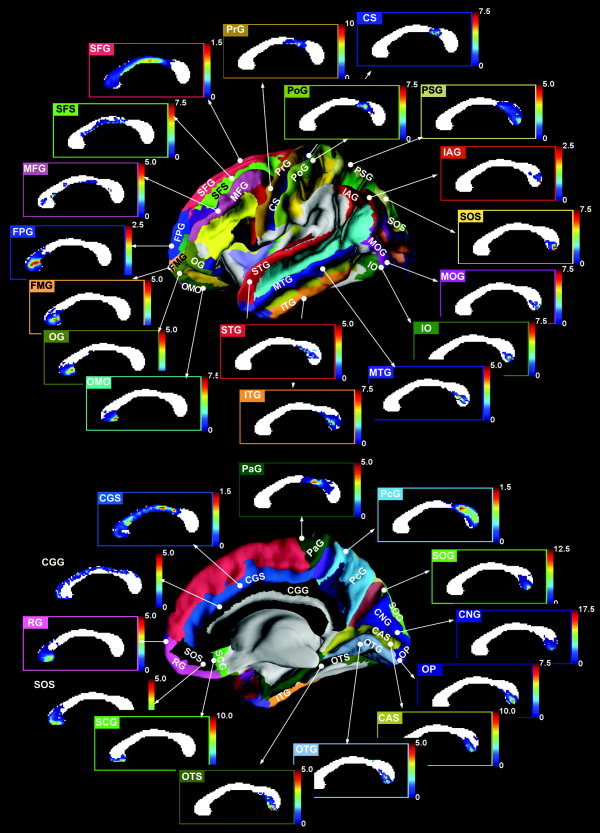
Statistical callosal topography based on the projection from cortical lobes. Callosal connection maps that explain topographic connection projected from given cortical lobes were derived from the dorsal prefrontal cortex, including the superior frontal gyrus (SFG), transverse frontopolar gyrus (FPG), superior frontal sulcus (SFS) and middle frontal gyrus (MFG), the ventral prefrontal cortex, including the rectus gyrus (RG), orbital medial/olfactory sulcus (OMO), orbital gyrus (OG), suborbital sulcus (SOS), frontomarginal gyrus (FMG), and subcallosal gyrus (SCG), the sensory‐motor cortex, including the paracentral gyrus (PaG), precentral gyrus (PrG), central sulcus (CS), and postcentral gyrus (PoG), the parietal cortex, including the precuneus gyrus (PcG), parietal superior gyrus (PSG), and parietal inferior gyrus angular part (IAG), the temporal cortex, including occipito‐temporal medial and lingual sulcus (OTS), inferior temporal gyrus (ITG), superior temporal gyrus (STG), and middle temporal gyrus (MTG), the occipital cortex, including the occipital pole (OP), occipital superior gyrus (SOG), calcarine sulcus (CAS), cuneus gyrus (CNG), occipito‐temporal medial gyrus lingual part (OTG), occipital superior and transversalis sulcus (SOS), occipital inferior gyrus and sulcus (IO), and occipital middle gyrus (MOG), and cingulated gyrus (CGG) and cingulate sulcus (CGS).
DISCUSSION
Population Topography of the CC
In this study, statistical connection maps of the CC were generated by combining diffusion tensor fiber tracking with structural gray matter parcellation in a group of healthy, young, right‐handed subjects. The basic premise is that cortical gray matter parcellations are interconnected through the white matter fiber bundles and therefore, precise parcellation of the gray matter using high resolution structural MRI can effectively be used for fiber bundle identification.
Except for the study by de Lacoste et al. [1985], little cytoarchitectonic research has been conducted on the connection‐based topography of the human CC. The work of de Lacoste et al. [1985] studied the CC topography by correlating the Wallerian degeneration distribution in the CC with focal cortical lesions. They found that fibers connecting the inferior frontal region to the anterior inferior parietal region pass through the rostrum and genu of the CC. In addition, fibers connecting the temporo‐parieto‐occipital junctional regions course through the splenium and caudal portion of the CC body. Finally, they found that the isthmus lies in the posterior CC body and contains fibers from the peri‐Sylvian region [de Lacoste et al., 1985]. However, this study has several limitations common to lesion‐based studies. From the13 brains with unilateral focal lesions and the 1 brain with 2 asymmetric lesions in separate hemispheres, only a small number (at most 2 single‐lesion brains or at most 4 multi‐lesion brains) of cortical subregions were used to identify the CC topography. Furthermore, the cortical lobes that were used were coarsely and broadly subdivided according to the specimen. For example, a subdivision of the cortical area started from the inferior prefrontal lobe and extended to the anterior inferior parietal lobe. When exploring the callosal connection from a cortical subregion, a small number of brains with a single lesion at the specific cortical subregion in addition to brains intermixed with multi‐lesions in different cortical subregions may not provide sufficient information to localize the CC connection.
Though a direct comparison is not possible because of differences in the sample specimens, sample size, spatial extent of the subregion, and methodologies, many of our results on the callosal distribution show similar patterns, if not exact consistency, to the lesion‐based work of de Lacoste et al. [1985]. In our study, axonal fibers connecting the ventro‐prefrontal cortex course through the genu and rostrum of the CC. The dorsal prefrontal lobes are interconnected from the upper part of the genu to the posterior body. In particular, the fibers connecting the superior frontal lobe extend into the posterior body and the anterior region of the isthmus of the CC. The sensory‐motor cortex projects fibers through the posterior mid‐body and the isthmus. Axons arising from the temporal cortex pass through the ventral isthmus or ventral splenium of the CC. While in contrast, axons from visual cortices, which occupy the greatest single fraction of the cortical mantle, pass through the pole or ventral part of the splenium of the CC. Finally, axons connecting the parietal lobes connect each hemisphere through the dorsal part of the splenium.
Near the CC body, we found a tendency for an axonal ordering similar to the results found in a cat study by Lomber et al. (1994). In the Lomber study, “while the antero‐posterior dimensions of the CC corresponded “point‐to‐point” to the antero‐posterior axis of the hemisphere, its dorso‐ventral dimension appeared to represent the medio‐lateral cortical axis in a nontopographical way” [Lomber et al., 1994].
Compared to the previous DT‐MRI fiber tracking studies [Abe et al., 2004; Huang et al., 2005a], our results show grossly similar results, but provide a more detailed resolution of the CC. These previous DT‐MRI‐based studies were limited by either restricted regions or coarse CC subdivisions using a rough definition of ROIs with a small number of subjects. In contrast, our populational callosal connection maps were derived from 22 young, healthy, right‐handed subjects and covered 47 cortical regions located mainly on the medial side of the whole brain. Considering the individual variation in cortical patterns [Park et al., 2004b] even in normal, healthy subjects, utilization of individual cortical parcellation enhanced the reliability of the topographic map and provided a more reliable way of parcellating individual CCs.
Dougherty et al. [2005] visualized the callosal connections of the occipital subregions derived from retinotopic maps using fMRI of four individual subjects. The four occipital lobe subdivisions used in this study for the exploration of the callosal distribution were dorsal V3, V3A, V3B and V7, dorsal V1 and V2, ventral V1 and V2, and ventral V3 and hV4. The study by Dougherty et al. used fMRI‐based occipital lobe subdivisions that were similar to the anatomical parcellations of the occipital lobe used in our study (i.e., occipital superior gyrus, cuneus gyrus, calcarine sulcus, and occipito‐temporal medial gyrus lingual part) (Fig. 3C). Because Dougherty et al. did not generate statistical topography of the four regions from the four individual subject maps, we are not able to directly compare their maps with our population‐based callosal topography maps. However, our results from the occipital lobe show similarities with their results in that callosal fibers projecting from these ROIs coursed through the ventral‐caudal part of the splenium with a tendency for higher to lower ordering depending on the location of the subregion.
In the current article, we displayed probabilistic population connection maps of 47 cortical gyri and sulci at the dorsal prefrontal cortex (7), ventral prefrontal cortex (7), sensory‐motor cortex (7), parietal cortex (6), cingulate (2), temporal cortex (9), and occipital cortex (9). Each map showed a certain amount of callosal connections from 64 cortical subregions. However, the cortical regions not displayed in Figure 3 might also have callosal connections, which were not detected in our study. The reason for this might be due to the limited information obtained from current DT‐MRI. For example, DT‐MRI might not show a connection of thin fiber bundles thinner than a voxel.
Considering the fact that several tissue structures may lie within a specific voxel and contribute to the formation of a single tensor at that particular voxel, we presented probabilistic connection of each cortex through the CC. As an indirect way to evaluate the applicability of the probabilistic connection maps to the individual data, the most dominant connection map of the group (Fig. 4B) was compared with individual dominant connection maps. The correspondence rate map in Figure 4E,F showed high correspondence at the body and dorsal splenium of the CC where fibers predominantly interconnect the superior frontal cortex and parietal cortex and showed low correspondence at the ventral splenium where fibers interconnect the temporal cortex. This correspondence rate in the highly reliable fiber tracking area could be useful in understanding the inter‐individual variability of the dominant callosal connection of individuals. However, in the area of low reliable and low sensitive fiber tracking, which corresponded with the area of high inter‐individual variability in our data, we considered that this inter‐individual variability in these areas could be largely attributed to the low reliability and low sensitivity of fiber tracking for individual data. Therefore, in the area of low correspondence rate, a group‐averaged representation of these callosal connections might represent individual callosal connection with higher reliability than the representation derived from fiber tracking of an individual. For this reason, the probabilistic connection maps of a healthy group displayed in Figure 3 have their peculiar advantages when compared with the discretized dominant connection map of a group (Fig. 4).
Because of the limitation of our methods, which are described in the next section, the population callosal connection maps derived from our study may require more validation and also may not completely replace the traditional Witelson's subdivision. However, we believe population callosal connection maps provide very useful information on the statistical distribution of the CC fibers based on their connectivity. Note that the information on callosal connection derived from a population of DT‐MRI data is not only noninvasive but also unique in that no other currently available methods could not easily provide the information on the connection.
Instead of the previous geometric subdivision by a vertical straight line, the genu and rostrum of the CC could be subdivided angularly (Figs. 3A and 4B). In addition, the CC splenium could be subdivided into dorsal and ventral sections. As compared with geometric subdivisions of the CC, this proposed subdivision of the CC is more consistent with the work by Oh et al. [2005], who subdivided the 80 boundary model‐based subdivision of the CC on the basis of homogeneity of the FA of diffusion tensor images. A more precise and systematic subdivision based on callosal connections should be further explored.
We should note that the cortical parcellation scheme [Fischl et al., 2004] used in our study was based not on cytoarchitecture, but on geometric features using outer anatomical landmarks determined by structural MRI. However, the existence of the discrepancy between the cytoarchitectonic subdivision and the MRI‐based subdivision at several cortical regions has been reported [Amunts et al., 2000; Geyer et al., 1999]. Therefore, the subdivisions in this study may not exactly match the cytoarchitectonic subdivisions. For example, frontal lobes are subdivided into the superior, middle, and frontal lobes according to their geometric shapes, but these divisions do not correspond with Broadmann's subdivision. The wide extent of CC which is occupied by fibers interconnecting the superior frontal cortex could be further subdivided if we could use subdivisions based on cytoarchitectonics. Further subclassifications of cortical regions may be required to achieve better matching using the cytoarchitectronic approach.
Methodological Considerations
The callosal fibers, especially fibers interconnecting the medial cortex, are the most well‐organized fibers in the brain and show relatively high reliability in fiber tracking when compared with other fiber bundles of the brain. Most of the connection maps in our study are based on these medial‐directing callosal fibers. However, we cannot disregard the limitations of fiber tracking, especially for fibers directed toward the lateral or inferior side of the brain. Because of partial volume and noise effects, voxels with intercrossing fibers of different pathways have increased uncertainty, which limits the tracking accuracy. Relative to other regions, the temporal lobe is located inferior and lateral to the CC. Fibers passing through these regions cross various directional fibers, such as internal capsule fibers and inferior longitudinal fascicles. Such fiber crossing may hinder the fiber bundles from correctly reaching the temporal lobe and may lead to the reduced reliability in fiber tracking.
To overcome fiber crossing problems, several streamline regularization algorithms have been proposed to penetrate ambiguous tensors [Weinstein et al., 1999; Westin et al., 2002]. However, streamline regularization fails to follow high curvature pathways, such as the CC pathway, because of the inertia component required for tracking [Lazar and Alexander 2003]. For this reason, the regularization method was not applied in our study. Recent techniques involving high angular resolution DT‐MRI [Tuch, 2004; Tuch et al., 2002] could be used to solve the fiber crossing problem and might show more accurate mapping of CC topography in the lateral regions.
Cardiac gating is one issue associated with the accuracy of fiber tracking. To reduce acquisition time and the associated motion artifacts in our study, DT‐MRI data were driven by a clinical setting for DT‐MRI acquisition without cardiac gating. According to previous reports on the effect of cardiac gating on the diffusion tensor image [Skare and Andersson, 2001; Wirestam et al., 1996], cardiac pulsation mainly affects the brain region below the CC. We thought most of the regions in our study were relatively unaffected by these artifacts. In addition to cardiac artifacts, there are several potential sources of error in fiber tracking, such as RF Johnson noise, eddy current, and susceptibility artifacts. Therefore, the population map of callosal connections consists of a topographic distribution of individual CCs from the group as well as a distribution of image distortion from various artifacts. However, since we can assume that the tracking error distribution was random across the subjects, the callosal map we generated can be considered reliable enough to represent the topography of the human callosal distribution.
We would like to note that each hemisphere contains neurons that project callosal axons to not only homologous (homotopic) areas in the contralateral hemisphere, but also to heterologous (heterotopic) areas [Di Virgilio and Clarke, 1997; Jones et al., 1979; Jones and Powell, 1969; Shanks et al., 1975]. In the current study, we could separate both homotopic and heterotopic fibers, and we could generate callosal connection maps using homotopic fibers (not presented in this article) and callosal connection maps using both homotopic and heterotopic fibers (presented in this article). We could not see a significant difference between these connection maps except for small changes in the scaling. Therefore, we decided not to separate homotopic and heterotopic fiber connections and we only took into account the fiber connections from the aspect of the mid‐sagittal section of the CC. Since the diffusion resolution (about 2 mm isocubic) is not enough to separate homotopic or heterotopic fibers, we thought it meaningless to compare a connection map based on the cortical origin of the callosal fibers with a map based on the contralateral cortical termination of these same fibers.
Our method can be applied to research on the functional association between hemispheres. One example of method application is the volumetric analysis of CC regions in relation to their connection with cortical lobes. The relationship between cortical volumes and the callosal area could provide important information regarding inter‐hemispheric connectivity. In clinical applications, our method could also play an important role in the research of callosal abnormalities, such as callosal dysgenesis [Lee et al., 2004], and could potentially provide additional information for the planning of local callosotomies.
CONCLUDING REMARKS
Our method used cortical gray matter parcellations in combination with diffusion tensor fiber tracking to subdivide the CC and generate statistical connection maps of the CC. This method is a more reliable way of evaluating CC connections with cortical lobes than using geometrical subdivision.
Acknowledgements
We thank Messrs. Maeng Geun Oh and Sei Young Kim for their excellent technical assistance.
REFERENCES
- Abe O, Masutani Y, Aoki S, Yamasue H, Yamada H, Kasai K, Mori H, Hayashi N, Masumoto T, Ohtomo K 2004: Topography of the human corpus callosum using diffusion tensor tractography. J Comput Assist Tomogr 28: 533–539. [DOI] [PubMed] [Google Scholar]
- Aboitiz F, Scheibel AB, Fisher RS, Zaidel E 1992: Fiber composition of the human corpus callosum. Brain Res 598: 143–153. [DOI] [PubMed] [Google Scholar]
- Alexander DC, Pierpaoli C, Basser PJ, Gee JC 2001: Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imaging 20: 1131–1139. [DOI] [PubMed] [Google Scholar]
- Amunts K, Malikovic A, Mohlberg H, Schormann T, Zilles K 2000: Brodmann's areas 17 and 18 brought into stereotaxic space‐where and how variable? Neuroimage 11: 66–84. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston K 1997: Multimodal image coregistration and partitioning—A unified framework. Neuroimage 6: 209–217. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C 1996: Microstructural and physiological features of tissues elucidated by quantitative‐diffusion‐tensor MRI. J Magn Reson B 111: 209–219. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A 2000: In vivo fiber tractography using DT‐MRI data. Magn Reson Med 44: 625–632. [DOI] [PubMed] [Google Scholar]
- Bishop KM, Wahlsten D 1997: Sex differences in the human corpus callosum: Myth or reality? Neurosci Biobehav Rev 21: 581–601. [DOI] [PubMed] [Google Scholar]
- Brun A, Knutsson H, Park HJ, Shenton ME, Westin CF 2004: Clustering fiber traces using normalized cuts. Medical Image Computing and Computer‐Assisted Intervention—MICCAI 2004, 368–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cipolloni PB, Pandya DN 1985: Topography and trajectories of commissural fibers of the superior temporal region in the rhesus monkey. Exp Brain Res 57: 381–389. [DOI] [PubMed] [Google Scholar]
- Clarke S, Kraftsik R, Van der Loos H, Innocenti GM 1989: Forms and measures of adult and developing human corpus callosum: Is there sexual dimorphism? J Comp Neurol 280: 213–230. [DOI] [PubMed] [Google Scholar]
- Conturo TE, Lori NF, Cull TS, Akbudak E, Snyder AZ, Shimony JS, McKinstry RC, Burton H, Raichle ME 1999: Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci USA 96: 10422–10427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Lacoste MC, Kirkpatrick JB, Ross ED 1985: Topography of the human corpus callosum. J Neuropathol Exp Neurol 44: 578–591. [DOI] [PubMed] [Google Scholar]
- Demeter S, Rosene DL, Van Hoesen GW 1990: Fields of origin and pathways of the interhemispheric commissures in the temporal lobe of macaques. J Comp Neurol 302: 29–53. [DOI] [PubMed] [Google Scholar]
- Denenberg VH, Kertesz A, Cowell PE 1991: A factor analysis of the human's corpus callosum. Brain Res 548: 126–132. [DOI] [PubMed] [Google Scholar]
- Di Virgilio G, Clarke S 1997: Direct interhemispheric visual input to human speech areas. Hum Brain Mapp 5: 347–354. [DOI] [PubMed] [Google Scholar]
- Dougherty RF, Ben‐Shachar M, Bammer R, Brewer AA, Wandell BA 2005: Functional organization of human occipital‐callosal fiber tracts. Proc Natl Acad Sci USA 102: 7350–7355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duara R, Kushch A, Gross‐Glenn K, Barker WW, Jallad B, Pascal S, Loewenstein DA, Sheldon J, Rabin M, Levin B, Lubs H 1991: Neuroanatomic differences between dyslexic and normal readers on magnetic resonance imaging scans. Arch Neurol 48: 410–416. [DOI] [PubMed] [Google Scholar]
- First MB, Spitzer RL, Gibbon M, Williams JBW 1996. Structured Clinical Interview for DSM‐IV Axis I Disorders (SCID). New York: New York State Psychiatric Institute, Biometrics Research; pp 380–382. [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM 2004: Automatically parcellating the human cerebral cortex. Cereb Cortex 14: 11–22. [DOI] [PubMed] [Google Scholar]
- Geyer S, Schleicher A, Zilles K 1999: Areas 3a, 3b, and 1 of human primary somatosensory cortex. Neuroimage 10: 63–83. [DOI] [PubMed] [Google Scholar]
- Guimond A, Meunier J, Thirion J‐P 2000: Average brain models: A convergence study. Comput Vis Image Underst 77: 192–210. [Google Scholar]
- Guimond A, Roche A, Ayache N, Meunier J 2001: Three‐dimensional multimodal brain warping using the demons algorithm and adaptive intensity corrections. IEEE Trans Med Imaging 20: 58–69. [DOI] [PubMed] [Google Scholar]
- Huang H, Zhang J, Jiang H, Wakana S, Poetscher L, Miller MI, van Zijl PC, Hillis AE, Wytik R, Mori S 2005: DTI tractography based parcellation of white matter: Application to the mid‐sagittal morphology of corpus callosum. Neuroimage 26: 195–205. [DOI] [PubMed] [Google Scholar]
- Jones EG, Powell TP 1969: Connexions of the somatic sensory cortex of the rhesus monkey II. Contralateral cortical connexions. Brain 92: 717–730. [DOI] [PubMed] [Google Scholar]
- Jones EG, Coulter JD, Wise SP 1979: Commissural columns in the sensory‐motor cortex of monkeys. J Comp Neurol 188: 113–135. [DOI] [PubMed] [Google Scholar]
- Jones DK, Simmons A, Williams SC, Horsfield MA 1999: Non‐invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI. Magn Reson Med 42: 37–41. [DOI] [PubMed] [Google Scholar]
- Kim DJ, Park H, Moon WJ, Chung EC, Kim IY, Kim SI 2005: Comparison of registration technologies for the evaluation of diffusion tensor imaging. Proceedings Annual meeting of The International Society for Magnetic Resonance in Medicine (ISMRM), May 7–13, 2005, Miami, FL.
- Lazar M, Alexander AL 2003: An error analysis of white matter tractography methods: Synthetic diffusion tensor field simulations. Neuroimage 20: 1140–1153. [DOI] [PubMed] [Google Scholar]
- Lee SK, Mori S, Kim DJ, Kim SY, Kim DI 2004: Diffusion tensor MR imaging visualizes the altered hemispheric fiber connection in callosal dysgenesis. AJNR Am J Neuroradiol 25: 25–28. [PMC free article] [PubMed] [Google Scholar]
- Lomber SG, Payne BR, Rosenquist AC 1994: The spatial relationship between the cerebral cortex and fiber trajectory through the corpus callosum of the cat. Behav Brain Res 64: 25–35. [DOI] [PubMed] [Google Scholar]
- Moeller FG, Hasan KM, Steinberg JL, Kramer LA, Dougherty DM, Santos RM, Valdes I, Swann AC, Barratt ES, Narayana PA 2005: Reduced anterior corpus callosum white matter integrity is related to increased impulsivity and reduced discriminability in cocaine‐dependent subjects: Diffusion tensor imaging. Neuropsychopharmacology 30(3): 610–617. [DOI] [PubMed] [Google Scholar]
- Mori S, Van Zijl PC 2002: Fiber tracking: Principles and strategies—A technical review. NMR Biomed 15: 468–480. [DOI] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, van Zijl PC 1999: Three‐dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 45: 265–269. [DOI] [PubMed] [Google Scholar]
- Oh JS, Suk PK, Chan SI, Ju KS, Hwang J, Chung A, Kyoon Lyoo I 2005: Fractional anisotropy‐based divisions of midsagittal corpus callosum. Neuroreport 16: 317–320. [DOI] [PubMed] [Google Scholar]
- Pandya DN, Karol EA, Heilbronn D 1971: The topographical distribution of interhemispheric projections in the corpus callosum of the rhesus monkey. Brain Res 32: 31–43. [DOI] [PubMed] [Google Scholar]
- Park HJ, Kubicki M, Shenton ME, Guimond A, McCarley RW, Maier M, Kikinis R, Jolesz FA, Westin CF 2003: Spatial normalization of diffusion tensor MRI using multiple channels. Neuroimage 20: 1995–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park HJ, Kubicki M, Westin CF, Talos IF, Brun A, Peiper S, Kikinis R, Jolesz FA, McCarley RW, Shenton ME 2004a: Method for combining information from white matter fiber tracking and gray matter parcellation. AJNR Am J Neuroradiol 25: 1318–1324. [PMC free article] [PubMed] [Google Scholar]
- Park HJ, Levitt J, Shenton ME, Salisbury DF, Kubicki M, Kikinis R, Jolesz FA, McCarley RW 2004b: An MRI study of spatial probability brain map differences between first‐episode schizophrenia and normal controls. Neuroimage 22: 1231–1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters M, Oeltze S, Seminowicz D, Steinmetz H, Koeneke S, Jancke L 2002: Division of the corpus callosum into subregions. Brain Cogn 50: 62–72. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP 1992: Numerical Recipes in C. Cambridge: Cambridge University Press. [Google Scholar]
- Seltzer B, Pandya DN 1983: The distribution of posterior parietal fibers in the corpus callosum of the rhesus monkey. Exp Brain Res 49: 147–50. [DOI] [PubMed] [Google Scholar]
- Shanks MF, Rockel AJ, Powell TP 1975: The commissural fibre connections of the primary somatic sensory cortex. Brain Res 98: 166–171. [DOI] [PubMed] [Google Scholar]
- Shin YW, Kim DJ, Ha TH, Park HJ, Moon WJ, Chung EC, Lee JM, Kim IY, Kim SI, Kwon JS 2005: Sex differences in the human corpus callosum: Diffusion tensor imaging study. Neuroreport 16: 795–798. [DOI] [PubMed] [Google Scholar]
- Skare S, Andersson JL 2001: On the effects of gating in diffusion imaging of the brain using single shot EPI. Magn Reson Imaging 19: 1125–1128. [DOI] [PubMed] [Google Scholar]
- Tench CR, Morgan PS, Blumhardt LD, Constantinescu C 2002: Improved white matter fiber tracking using stochastic labeling. Magn Reson Med 48: 677–683. [DOI] [PubMed] [Google Scholar]
- Tuch DS 2004: Q‐ball imaging. Magn Reson Med 52: 1358–1372. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ 2002: High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn Reson Med 48: 577–582. [DOI] [PubMed] [Google Scholar]
- Weinstein DM, Kindlmann GL, Lundberg EC 1999: Tensorlines: Advection‐Diffusion Based Propagation Through Diffusion Tensor Fields. IEEE Visualization Proc. San Francisco: pp 249–253. [Google Scholar]
- Westin CF, Maier SE, Mamata H, Nabavi A, Jolesz FA, Kikinis R 2002: Processing and visualization for diffusion tensor MRI. Med Image Anal 6: 93–108. [DOI] [PubMed] [Google Scholar]
- Wirestam R, Greitz D, Thomsen C, Brockstedt S, Olsson MB, Stahlberg F 1996: Theoretical and experimental evaluation of phase‐dispersion effects caused by brain motion in diffusion and perfusion MR imaging. J Magn Reson Imaging 6: 348–355. [DOI] [PubMed] [Google Scholar]
- Witelson SF 1989: Hand and sex differences in the isthmus and genu of the human corpus callosum. A postmortem morphological study. Brain 112 (Part 3): 799–835. [DOI] [PubMed] [Google Scholar]
- Woods RP, Cherry SR, Mazziotta JC 1992: Rapid automated algorithm for aligning and reslicing PET images. J Comput Assist Tomogr 16: 620–633. [DOI] [PubMed] [Google Scholar]
- Xu D, Mori S, Solaiyappan M, van Zijl PC, Davatzikos C 2002: A framework for callosal fiber distribution analysis. Neuroimage 17: 1131–1143. [DOI] [PubMed] [Google Scholar]


