Figure 5.

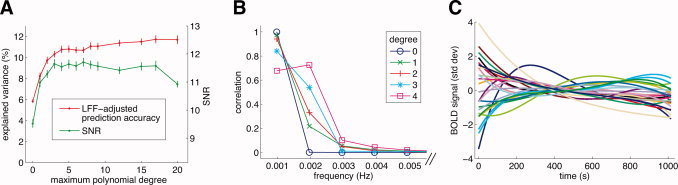
Characteristics of LFF. (A) The effect of the maximum polynomial degree on model performance. We manipulated the maximum degree of the polynomials included in the POLY model (x‐axis) and evaluated the effect on LFF‐adjusted prediction accuracy (y‐axis; red line) and SNR (y‐axis; green line). For this graph we selected voxels with a minimum SNR of 10 under any of the model variants (n = 2,890). Dots indicate the median across voxels, and error bars indicate ±1 SE (bootstrap procedure). With increasing polynomial degree, both LFF‐adjusted prediction accuracy and SNR dramatically increased. (B) Spectral content of Legendre polynomials of degrees 0 through 4. The polynomials extend over the course of the time‐series data (17 min). We calculated the discrete Fourier transform of each polynomial after applying a Hanning window to avoid edge artifacts and subtracting the mean value. The correlation (y‐axis) between the time‐series data and the Fourier component at each frequency (x‐axis) is plotted. For display purposes the zero‐frequency point is omitted. Note that the polynomials consist predominantly of very low frequencies (0–0.004 Hz). (C) Example timecourses of LFF. For 25 voxels we plot nuisance effects as determined under the POLY model. These voxels were randomly selected from voxels with a minimum SNR of 10 (n = 1,730). The x‐axis indicates time; the y‐axis indicates standard deviation units (see Methods). For display purposes, the mean of each timecourse is removed.