Abstract
The dorsolateral prefrontal cortex (DLPFC) has been implicated in the pathophysiology of several psychiatric illnesses including major depressive disorder and schizophrenia. In this regard, the DLPFC has been targeted in repetitive transcranial magnetic stimulation (rTMS) studies as a form of treatment to those patients who are resistant to medications. The ‘5‐cm method’ and the ‘10‐20 method’ for positioning the transcranial magnetic stimulation (TMS) coil over DLPFC have been scrutinised due to poor targeting accuracies attributed to inter‐subject variability. We evaluated the accuracy of such methods to localise the DLPFC on the scalp in 15 healthy subjects and compared them with our novel neuronavigational method, which first estimates the DLPFC position in the cortex based on a standard template and then determines the most appropriate position on the scalp in which to place the TMS coil. Our neuronavigational method yielded a scalp position for the left DLPFC between electrodes F3 and F5 in standard space and was closest to electrode F5 in individual space. Further, we found that there was significantly less inter‐subject variability using our neuronavigational method for localising the DLPFC on the scalp compared with the ‘5‐cm method’ and the ‘10‐20 method’. Our findings also suggest that the ‘10‐20 method’ is superior to the ‘5‐cm method’ in reducing inter‐subject variability and that electrode F5 should be the stimulation location of choice when MRI co‐registration is not available. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.
Keywords: DLPFC, TMS coil placement, 5‐cm rule, EEG coordinates, neuronavigation, MDD
INTRODUCTION
The abnormal functioning of the dorsolateral prefrontal cortex (DLPFC) has been implicated in the pathophysiology of several neuropsychiatric disorders including major depressive disorder (MDD) and schizophrenia. Moreover, such deficits in DLPFC functioning have been related to symptom severity and serves as a target for repetitive transcranial magnetic stimulation (rTMS) as an alternative treatment. Given the promising success of rTMS over the DLPFC in alleviating symptoms associated with MDD and schizophrenia, advancement in improving the localisation of this brain region is invaluable to optimising rTMS as a potential treatment.
Over the past decade the ‘5‐cm method’ has been routinely used for targeting the DLPFC in transcranial magnetic stimulation (TMS) studies. With this method, the DLPFC is localised by stimulating the motor cortex and recording motor evoked potentials in the contralateral hand muscle (i.e., abductor pollicis brevis; APB), and then measuring 5 cm anterior from this position along a parasaggital line [George et al., 1995; Pascual‐Leone et al., 1996]. Although the ‘5‐cm method’ is easy to perform without the cost of expensive neuronavigational techniques, it has been criticised for its failure to take into account cortex morphology and often yield positions that fall too short [Herwig et al., 2001]. For example, an MRI‐based neuronavagational study reported that the ‘5‐cm method’ was found to correspond to Brodman's area (BA) 6 (pre‐motor cortex) or 8 (frontal eye field) in 15/22 subjects, while a position within BA 9 was found in the other seven subjects. Such inter‐individual variation for identifying the DLPFC through the ‘5‐cm method’ is thought to be a result of both variations in the distance between the motor areas and the DLPFC, and also low inter‐rater reliability in determining this distance. Most importantly, such variability may also account for inconsistent therapeutic results when using repetitive TMS (rTMS) over the DLPFC to treat patients with MDD. For example, a recent study examined DLPFC location variability of the ‘5‐cm method’ with rTMS anti‐depressive effects and found significantly reduced depression scores in individuals with DLPFC positions that were more lateral and anterior [Herbsman et al., 2009]. Furthermore, our group showed that targeted rTMS to DLPFC functional coordinates guided by a meta‐analysis on neuorimaging studies on working memory in MDD patients [Fitzgerald et al., 2006] resulted in greater anti‐depressive effects compared to the ‘5‐cm method’ [Fitzgerald et al., 2009]. Together these studies demonstrate the pitfalls of the ‘5‐cm method’ and provide clear support for the need for better localisation techniques that are less susceptible to inter‐subject and inter‐rater variability to optimise rTMS as a treatment for MDD.
The international 10‐20 system [Jasper, 1958] that is typically used in electroencephalography (EEG) electrode placement has proven useful in linking external scalp locations to underlying cortex. To this end, previous studies have used the 10‐20 system to target the left and right DLPFC by placing the TMS coil over the F3 and F4 electrode, respectively [Gerloff et al., 1997; Rossi et al., 2001]. Herwig et al. [ 2003] provided further support in ascribing F3 and F4 from the 10‐20 system to the underlying DLPFC cortical area [Herwig et al., 2003]. In their study, 21 subjects were co‐registered with an EEG cap and dynamic reference frame mounted on their head. With their neuronavigational technique based on frameless stereotaxy, a probe was placed over electrodes F3 and F4 and its position projected 15 mm down to the underlying cortex to provide X, Y, and Z coordinates in individual space. The authors then used a Talairach atlas to relate individual coordinates to Talairach coordinates (x, y, z) = −37, 27, 44 for the left DLPFC, which corresponded to the dorsal and superior edge of BA 9, bordering BA 8 in standardised space. The findings by Herwig et al. [ 2003], therefore, were consistent with previous studies [Gerloff et al., 1997; Rossi et al., 2001] that identified electrode F3 as the closest electrode to target the left DLPFC. Although using the F3 electrode (‘10‐20 method’) to represent the left DLPFC may be an improvement from the conventional ‘5‐cm method’, it is still limited in several ways. First, as the DLPFC is a functional area, a comparison between an individual T1‐weighted MRI and the Talairach atlas may not adequately identify this area. Second, while the ‘10‐20 method’ takes into account head size, it does not take into account head shape, an important consideration in studies using rTMS therapeutically. Third, this method also does not take into consideration the morphology of the underlying cortex so that simply placing TMS coil over F3 to target the left DLPFC is less than ideal. By contrast, localising the DLPFC based on functional standardised coordinates (e.g., Talairach or MNI coordinates) and then determining its relative location on the scalp for TMS coil placement may enhance the likelihood that the desired cortical region is activated. This study, therefore, was designed to evaluate the accuracy of previous methods to localise the DLPFC compared to our novel neuronavigational method, which first estimates the cortical position based on a standard template and then determines the most appropriate position for the TMS coil on the scalp in healthy subjects.
MATERIALS AND METHODS
Fifteen right‐handed healthy volunteers were tested (mean age, 35.1 years; SD, 7.77 years; range, 24–49 years; 10 men and 5 women). Subjects gave their written informed consent and the protocol was approved (Centre for Addiction and Mental Health in accordance with the declaration of Helsinki). Exclusion criteria included psychiatric or medical illness, a history of drug or alcohol abuse.
Procedure
Magnetic resonance image
A T‐1 weighted magnetic resonance image (MRI) (Acquisition Type = 3D, TR = 8.892 ms, TE = 1.792 ms, Inversion Time = 300, Number of Averages = 1, Slice Thickness = 1.5, FOV = 20 cm, Matrix = 256 × 256) was acquired for all subjects with seven fiducial markers in place for future co‐registration. The images were converted to isotropic voxels of side 0.86 mm and the position of the anterior commissure (AC) was identified. The images were then stored in 16 bits with values ranging from 0 to 3,000. A threshold value of 250 defined the iso‐surface representing the scalp.
Functional coordinates for the left DLPFC
The results from recent meta‐analyses on functional neuroimaging studies testing working memory in patients with depression and schizophrenia [Fitzgerald et al., 2006; Glahn et al., 2005; Mendrek et al., 2005; Tan et al., 2005] were used to identify the functional region of the left DLPFC. These studies, however, localised the left DLPFC to an area within the anterior portion of the medial prefrontal cortex at the juncture of BA 9/46, and did not specify a single coordinate position. Although a study conducted earlier by our group examined rTMS applied to DLPFC position using (x, y, z) = −45, 45, 35 in Talairach coordinates [(x, y, z) = −46, 45, 38 MNI coordinates] resulted in greater reduction in depressive scores in MDD patients, this does not preclude that other voxel positions within this juncture may more optimally improve the antidepressant effects of rTMS in MDD patients. As such, we selected the coordinate (x, y, z) = −50, 30, 36 after converting these coordinates to MNI space that also corresponded to the juncture of BAs 9 and 46. Our DLPFC coordinate (x, y, z) = −50, 30, 36 mm resulted in a position that was a little more posterior and lateral to those examined by Fitzgerald et al. [ 2009].
Optimal TMS coil placement for targeting the left DLPFC
Importantly, the neuronavigational method used to position the TMS coil on the scalp in this study, can be applied to any cortical coordinates in the brain. It involved two steps: we first found the position of the left DLPFC on the cortex of each subject (DLPFCC) based on the normalisation of a template, followed by the application of a marching cubes algorithm to find the optimal position for the coil on the scalp (DLPFCS; Fig. 1). These procedures were done for all 15 subjects included in this study.
Figure 1.
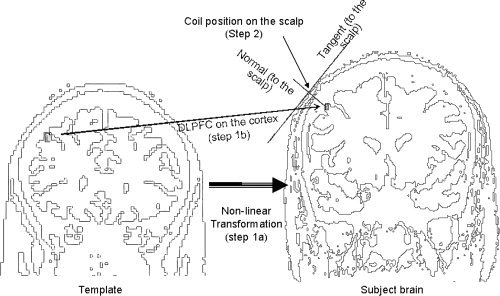
A non‐linear transformation to convert the coordinates from a standard space to an individual space was first estimated (Step 1A). This estimated transform was then applied to the coordinates for the DLPFC in the standard brain (or template) to determine the position of the DLPFC in the individual brain (Step 1B). Next, a triangular mesh wrapping the iso‐surface representing the scalp was created with the marching cube algorithm (see Methods). The optimal position for the coil (mDLPFCS) on the scalp was then defined as the vertex of the triangular mesh with a normal that passed through the DLPFC on the cortex (DLPFCC; Step 2).
Estimating the left DLPFC on the cortex (DLPFCC)
First, the DLPFC (x, y, z = −50, 30, 36; MNI brain) was identified on the brain template MNI/ICBM 152 [Evans, 1993; Mazziotta et al., 2001] by meta‐analyses on neuroimaging studies examining working memory in patients with MDD and schizophrenia [Fitzgerald et al., 2006; Glahn et al., 2005; Mendrek et al., 2005; Tan et al., 2005]. These coordinates were also shown to result in superior therapeutic efficacy in MDD when targeted through rTMS compared to the ‘5‐cm method’ [Fitzgerald et al., in press]. For each subject, the best non‐linear transform to map the standard brain to each individual brain was estimated using the subroutine spm_normalize from the SPM2 (http://www.fil.ion.ucl.ac.uk/spm/; [Ashburner and Friston, 1999; Ashburner et al., 1997]. Next, the coordinates for the DLPFCC in individual brains were estimated by applying the resulting transformation to the coordinates of the DLPFCC in the template (Fig. 1; Step 1A).
Estimating the position of the left DLPFC on the scalp (DLPFCS)
The DLPFCS on the scalp was defined as the position in which the tangential plane to the scalp had a perpendicular (called normal) that passed through the DLPFCC. The position on the surface of the scalp was estimated using a classic algorithm for rendering called marching cubes [Lorensen, 1987] followed by a selection process. To use the marching cubes algorithm, a threshold value of 250 (the value‐tone colour at the border of the scalp) was chosen to define an iso‐surface on the MRI representing the scalp. The marching cubes algorithm (http://local.wasp.uwa.edu.au/~pbourke/geometry/polygonise/) generates a triangular mesh (a set of 3‐3D coordinates) rendering this 3D surface on the image. Note that in actuality this threshold value defines three surfaces in a T1 contrast: the exterior surface of the scalp, the interior surface of the skull and the surface of the cortex. In addition, to create the triangular mesh, this version of the marching cube algorithm determined a normal to the iso‐surface at each vertex of the mesh by averaging the normals to the faces of all the triangles that shared this vertex.
The selection process to determine the location of the DLPFCC on the scalp consisted of seven sequential steps:
-
1
The coordinates of each vertex was associated with the closest voxel and only the voxels with a normal that intersected a sphere of 3 mm around the DLPFCC at a distance less than 3 cm were considered.
-
2
For each voxel (i) the average distance (
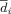) to the other voxels were calculated. If 
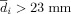, the voxel (i) was filtered out. This filtering process was necessary to remove voxels that were generated by the marching cubes algorithm that were further from the main cluster and were likely to be outliers. -
3
A second filter was then used to remove voxels that were within 1.5 cm of the DLPFCC, as these voxels were most likely to be on the cortex rather than the scalp.
-
4
Next, an average normal from all of the ensuing voxels (Fig. 2A) was calculated, and those voxels with a normal that formed an angle greater than 25° with respect to the average were removed.
-
5
An average position and normal was then calculated from the remaining vertices.
-
6
A 3D image of a 6‐cm line that represented a normal to the scalp (estimated in Step 5) which also passed through the middle point of the vertices' mean position was then superimposed on the MRI image. As quality control this line should have passed through the DLPFCC.
-
7
The position of the coil on the scalp (DLPFCS) was then determined manually by selecting one point on this 3D line, which fell on the scalp. A spherical mark with a diameter of 2.5 mm (i.e., small than a fiducial mark) was then superimposed on the MRI image for later co‐registration of the MRI image (Fig. 2B). The position for the DLPFCS predicted through our method will be called ‘method’ DLPFCS (mDLPFCS), while this position is referred to as the ‘experimental’ DLPFCS (eDLPFCS) once it is co‐registered to the subjects' MRI, representing its true position on the scalp.
Figure 2.
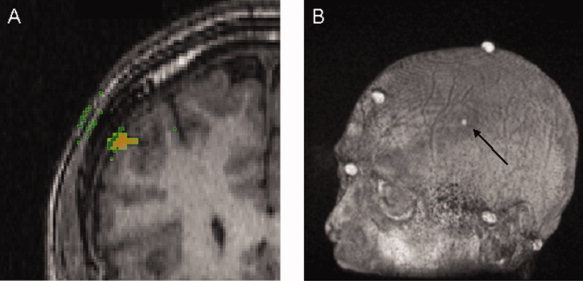
A: In this coronal slice of a MRI image, the orange spot represents the DLPFC on the cortex (DLPFCC) and the green squares are voxels on the iso‐surface with a normal that passes through the DLPFCC in a distance less than 3 cm. Voxels (green squares) on surfaces other than the scalp (i.e., the internal side of the skull, and the interface grey matter‐CSF) were filtered out if they had a normal greater than 25° from the average normal. The mDLPFCS was defined as the intersection of the scalp with a line with the orientation of the average normal and passes through their average position. B: The position of mDLPFCS was superimposed on each individual's MRI for later co‐registration. Once mDLPFCS is co‐registered, this position is referred to as the eDLPFCS.
MRI co‐registration
Prior to MRI co‐registration, a 64 channel EEG cap (STIM2, Neuroscan, USA) was placed on the subjects' head to mark the positions of electrodes AF3, F3, F5, FC3 and FC5 (‘10‐20 method’) with an ink‐filled syringe. The EEG cap was then removed for identification of the ‘5‐cm method’.
In accordance to the ‘5‐cm method’ to localise the DLPFC, single monophasic TMS pulses (Magstim Company Ltd., UK) were administered to the left APB of the motor cortex, while resulting electromyography activity was collected using commercially available software, Signal (Cambridge Electronics Design, UK). A felt pen was then used to mark the optimal position under the centre of the coil for eliciting motor evoked potentials from this muscle (APB) and the location of the DLPFC was measured 5 cm anterior from this position.
Neuronavagational techniques (MINIBIRD system; Ascension Technologies) combined with MRIcro/reg software were first used to co‐register the 7 fiducial markers to subjects' MRI with the position of the mDLPFCS superimposed on the image (represented as a sphere in Fig. 2B). The position of the DLPFCS was then marked on the subjects' scalp and its experimental coordinates recorded, and referred to as eDLPFCS. Next, the positions marked on the scalp for APB, ‘5‐cm method’, AF3, F3, F5, FC3 and FC5 electrodes (‘10‐20 method’) were registered to the image and their coordinates recorded. These coordinate positions were then translated to the MNI/ICBM using an affine transformation from the individual brain to the template (i.e., the inverse of the affine transformation that was first used in the non‐linear transformation to estimate DLPFCC). Finally, the positions APB, ‘5‐cm method’, and AF3, F3, F5, FC3, FC5 electrodes (‘10‐20 method’) relative to the eDLPFCS were also measured to provide data in individual space.
Software implementation
The algorithms were programmed in C++ and integrated in a friendly graphic user interface. SPM ran under MATLAB (The MathWorks, Inc. Natick, MA), called from the C++ via the API interface. In total our method takes ∼5 min with most of the time allotted to selecting the voxel location of the mDLPFCS (Step 7). The automated steps are practically instantaneous with any current hardware. Software is available by request via e‐mail to pablo.rusjan@camhpet.ca.
Data analysis
To evaluate the inter‐subject variability found between all of the methods (i.e., ‘5‐cm method’, ‘10‐20 method’ and our method), a jackknife approach was used for each ellipsoid volume representing the dispersion (N = 15) of each landmark:
-
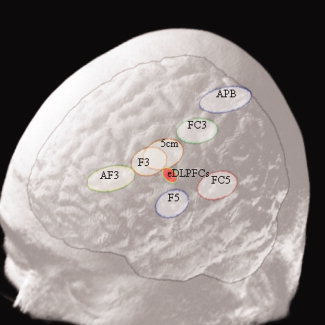
1The mean position and the standard deviation of each dimension (σ,σ,σ) for each method (condition) in each sub sample (j), by leaving one subject (j) out of the jackknife, where j = 1–15 was calculated. The standard deviations were then used to estimate the dispersion as the volume of an ellipsoid:
-
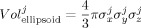
2
The difference between the dispersion of methods within each sub sample was then calculated as the difference of ellipsoid volume.
-
3
Finally, Wilcoxon non‐parametric signed‐rank tests were used to determine whether the volumes derived under each method (i.e., the three‐dimensional amount of variability in estimates) differed. A non‐parametric approach seemed more appropriate than a series of paired t‐tests, since the assumptions underlying parametric tests most likely would not have been met due to our sample size limitation. In addition, it may not have been appropriate to assume that the distributional properties of the composite standard deviation volume measurements were normally distributed.
RESULTS
Individual Space
The positions of APB, the ‘5‐cm method’, and electrodes AF3, F3, F5, FC3 and FC5 (‘10‐20 method’) relative to the eDLPFCS were measured with a measuring tape and are shown in Table I. These measures are not normalised by head size, and thus, provide an evaluation of both the ‘5‐cm method’ and the ‘10‐20 method’ to localise the left DLPFC in individual space. The average distance from APB to the eDLPFCS was ∼5.3 cm, ranging from 3.0 to 7.3 cm in 15 subjects. Although 5.3 cm is close to 5 cm, this position was not on the same sagittal plane as the position given for the ‘5‐cm method’, and the average distance between these two landmarks was 2.6 cm. In evaluating the ‘10‐20 method’ to localise the left DLPFC, we found that F5 was the closest electrode to eDLPFCS with a mean difference of 1.9 cm, followed by electrodes FC5 (2.3 cm) and F3 (2.8), respectively (Table I). Table II, compares the voxel coordinates predicted by our method (i.e., Fig. 2B) mDLPFCS with the position obtained with the co‐ registration probe during the experiment, referred to as eDLPFCS. Further, the difference between these two positions was 12.6 mm with the x‐direction (left‐right) driving this difference. More explicitly, the experimental coordinates were found to be more lateral (i.e., more exterior) than the centre of the fake fiducial marking the position of mDLPFCS (see Fig. 3, same result in standardised space). This discrepancy may reflect some systematic bias of the method (i.e., manual selection of the voxel representing mDLPFCS) that could be related to the intrinsic spatial resolution pattern of the MINIBIRD system, accuracy of the co‐registration procedures or the need to take into account the physical characteristics of the scalp (i.e., amount of hair on the scalp, size of the probe). As such, the difference between these two locations (i.e., mDLPFCS and eDLPFCS) will be statistically tested in standardised space to account for differences arising from head size and MRI orientation.
Table I.
Actual distance (cm) from the experimental location of left DLPFC (eDLPFCS) to EEG electrodes, APB, and the ‘5‐cm method’ on the scalp in all 15 healthy subjects in individual space
| ID | APB | 5 cm | F3 | F5 | FC3 | FC5 | AF3 |
|---|---|---|---|---|---|---|---|
| 1 | 7.00 | 2.50 | 2.00 | 0.80 | 5.20 | 3.50 | 3.50 |
| 2 | 7.30 | 2.00 | 1.00 | 2.50 | 4.50 | 4.50 | 2.30 |
| 3 | 4.50 | 1.50 | 2.80 | 2.30 | 3.00 | 1.60 | 5.00 |
| 4 | 3.00 | 3.20 | 2.40 | 2.30 | 1.70 | 2.80 | 5.20 |
| 5 | 5.00 | 2.80 | 3.20 | 1.00 | 4.00 | 1.50 | 5.00 |
| 6 | 5.50 | 3.00 | 4.00 | 2.50 | 3.30 | 1.00 | 6.00 |
| 7 | 5.10 | 3.40 | 4.00 | 2.00 | 4.00 | 1.20 | 6.00 |
| 8 | 6.00 | 2.40 | 2.00 | 2.00 | 2.50 | 2.20 | 4.50 |
| 9 | 6.00 | 1.20 | 0.70 | 2.50 | 3.80 | 4.50 | 1.80 |
| 10 | 6.50 | 1.80 | 2.00 | 2.70 | 1.50 | 3.00 | NaN |
| 11 | 5.00 | 0.80 | 1.50 | 2.50 | 4.00 | 5.00 | 2.50 |
| 12 | 6.50 | 1.20 | 1.20 | 3.00 | 2.80 | 4.50 | 4.00 |
| 13 | 5.40 | 0.60 | 2.00 | 1.20 | 3.00 | 2.50 | 4.00 |
| 14 | 6.30 | 2.70 | 1.50 | 1.50 | 3.00 | 3.80 | 3.20 |
| 15 | 5.50 | 1.00 | 1.20 | 2.00 | 3.30 | 3.40 | 4.00 |
| Mean | 5.34 | 2.63 | 2.77 | 1.91 | 3.67 | 2.30 | 4.71 |
| Std dev | 1.47 | 0.68 | 1.09 | 0.72 | 1.13 | 1.33 | 1.35 |
Table II.
A comparison showing the voxel coordinates predicted by our method (mDLPFCS) with the voxel coordinates obtained during the experiment with the co‐registration probe (eDLPFCS) in individual space
| ID | DLPFC experimental (vxl) | DPLFC method (vxl) | Difference (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | Length | |
| 1 | 52 | 161 | 164 | 58 | 166 | 165 | 5.2 | 4.3 | 0.9 | 6.8 |
| 2 | 56 | 157 | 169 | 57 | 178 | 152 | 0.9 | 18.1 | −14.6 | 23.3 |
| 3 | 44 | 127 | 160 | 54 | 127 | 163 | 8.6 | 0.0 | 2.6 | 9.0 |
| 4 | 57 | 147 | 156 | 61 | 150 | 158 | 3.4 | 2.6 | 1.7 | 4.6 |
| 5 | 42 | 151 | 151 | 63 | 152 | 152 | 18.1 | 0.9 | 0.9 | 18.1 |
| 6 | 45 | 158 | 160 | 61 | 158 | 162 | 13.8 | 0.0 | 1.7 | 13.9 |
| 7 | 40 | 155 | 146 | 61 | 155 | 148 | 18.1 | 0.0 | 1.7 | 18.1 |
| 8 | 59 | 155 | 153 | 62 | 157 | 153 | 2.6 | 1.7 | 0.0 | 3.1 |
| 9 | 46 | 167 | 156 | 70 | 169 | 152 | 20.6 | 1.7 | −3.4 | 21.0 |
| 10 | 44 | 169 | 151 | 61 | 167 | 149 | 14.6 | −1.7 | −1.7 | 14.8 |
| 11 | 37 | 161 | 155 | 61 | 163 | 153 | 20.6 | 1.7 | −1.7 | 20.8 |
| 12 | 72 | 149 | 162 | 70 | 149 | 166 | −1.7 | 0.0 | 3.4 | 3.8 |
| 13 | 56 | 154 | 145 | 65 | 155 | 145 | 7.7 | 0.9 | 0.0 | 7.8 |
| 14 | 38 | 148 | 161 | 52 | 147 | 158 | 12.0 | −0.9 | −2.6 | 12.3 |
| 15 | 56 | 156 | 161 | 70 | 157 | 163 | 12.0 | 0.9 | 1.7 | 12.2 |
| Average | 10.4 | 2.0 | −0.6 | 12.6 | ||||||
| Std dev | 7.3 | 4.7 | 4.3 | 6.7 | ||||||
Figure 3.
Although the position predicted by our method (mDLPFCS; green) is placed on the subjects' scalp, the actual position measured with the probe when co‐registered (eDLPFCS; orange) is biased in the radial direction. These positions are shown for all subjects in MNI space.
Standardised Space
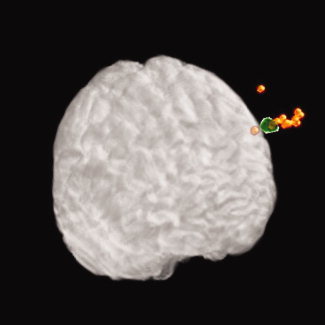
In standardised space, the closest position to eDLPFCS was found with the ‘5‐cm method’ (Table III). However, the average distance of eDLPFCS to APB was ∼7 cm and not along a parasaggital line as in the ‘5‐cm method’. Figure 4 illustrates that DLPFCS corresponds best to a position more lateral, inferior and posterior than F3, and superior to F5. Wilcoxon non‐parametric signed‐rank tests were then performed to evaluate the inter‐subject variability in ‘5‐cm method’ and the ‘10‐20 method’ compared to our method (SAS System v.9.1.3; SAS Institute, NC). Our method yielded the least amount of variation compared to the ‘5‐cm method’ (P < 0.0001) and compared with the ‘10‐20 method’ (P < 0.0001) for both electrodes F3 and F5, respectively. In addition, less inter‐subject variability was found with ‘10‐20 method’ compared with the ‘5‐cm method’ (P = 0.0002, electrode F3; P ≈ 0.000, electrode F5, respectively). Finally, with all three methods, a greater standard deviation was observed in the anterior‐posterior direction that may be reflective of the pattern of spatial resolution of the MINIBIRD; however, our method still yielded the least inter‐subject variability for eDLPFCS compared positions generated by the other methods.
Table III.
Positions in standardized MNI space (mm) for each subject predicted by the method (mDLPFCS) compared with positions measured during the experiment (eDLPFCS)
| ID | Method | Experimental | APB | 5 cm | F3 | F5 | FC3 | FC5 | AF3 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | ||||
| 1 | −59 | 37 | 46 | −65 | 33 | 47 | −53 | −35 | 89 | −56 | 13 | 68 | −49 | 31 | 66 | −71 | 27 | 40 | −54 | −5 | 82 | −80 | −6 | 52 | −32 | 55 | 52 |
| 2 | −60 | 36 | 47 | −61 | 19 | 67 | −45 | −36 | 78 | −52 | 19 | 66 | −53 | 23 | 58 | −78 | 15 | 29 | −45 | −17 | 71 | −74 | −18 | 42 | −42 | 50 | 43 |
| 3 | −62 | 32 | 45 | −71 | 31 | 43 | −59 | 2 | 82 | −60 | 43 | 54 | −54 | 51 | 51 | −70 | 41 | 25 | −59 | 21 | 75 | −79 | 16 | 37 | −38 | 69 | 38 |
| 4 | −59 | 34 | 45 | −62 | 31 | 44 | −46 | −73 | 102 | −47 | 62 | 33 | −50 | 52 | 38 | −68 | 45 | 12 | −62 | 16 | 59 | −77 | 16 | 31 | −39 | 73 | 30 |
| 5 | −58 | 35 | 45 | −70 | 32 | 46 | −58 | −23 | 80 | −67 | 27 | 51 | −62 | 31 | 54 | −78 | 18 | 30 | −63 | −6 | 70 | −86 | −12 | 38 | −49 | 5 | 50 |
| 6 | −58 | 31 | 46 | −72 | 31 | 43 | −58 | −7 | 85 | −55 | 39 | 69 | −52 | 64 | 48 | −70 | 52 | 26 | −58 | 31 | 73 | −79 | 26 | 45 | −35 | 83 | 30 |
| 7 | −60 | 34 | 44 | −79 | 33 | 43 | −56 | 11 | 94 | −55 | 60 | 58 | −55 | 64 | 65 | −69 | 53 | 38 | −61 | 30 | 86 | −81 | 24 | 56 | −36 | 75 | 47 |
| 8 | −59 | 35 | 46 | −62 | 33 | 46 | 37 | 33 | 91 | 50 | 20 | 69 | 56 | 42 | 50 | 74 | 31 | 28 | 57 | 1 | 74 | 81 | 3 | 42 | 44 | 65 | 33 |
| 9 | 57 | 35 | 45 | 81 | 31 | 50 | 75 | 22 | 88 | 78 | 26 | 60 | 83 | 27 | 55 | 90 | 21 | 24 | 93 | 5 | 64 | 102 | 13 | 27 | ‐67 | 50 | 39 |
| 10 | 61 | 34 | 45 | 77 | 36 | 47 | 51 | 23 | 79 | 66 | 25 | 58 | 53 | 49 | 57 | 77 | 37 | 37 | 62 | 20 | 71 | 88 | 7 | 40 | 39 | 77 | 36 |
| 11 | 58 | 36 | 46 | 81 | 36 | 49 | 58 | 11 | 83 | 60 | 26 | 57 | 60 | 23 | 65 | 77 | 17 | 33 | 69 | 8 | 69 | 92 | 15 | 31 | 52 | 61 | 51 |
| 12 | 59 | 31 | 47 | 50 | 30 | 43 | 53 | 45 | 75 | 56 | 10 | 48 | 59 | 38 | 38 | 65 | 14 | 8 | 59 | 8 | 62 | 70 | 21 | 20 | |||
| 13 | 62 | 34 | 44 | 71 | 32 | 45 | 64 | 29 | 80 | 66 | 16 | 58 | 49 | 41 | 63 | 72 | 34 | 40 | 54 | 12 | 73 | −80 | 10 | 40 | −44 | 62 | 46 |
| 14 | −56 | 34 | 46 | −68 | 37 | 50 | −44 | −24 | 92 | −56 | 29 | 73 | −60 | 35 | 64 | −76 | 28 | 36 | −63 | 1 | 76 | −85 | −7 | 44 | −46 | 57 | 42 |
| 15 | −61 | 33 | 45 | −74 | 31 | 43 | −69 | −10 | 79 | −66 | 35 | 54 | −63 | 43 | 48 | −76 | 35 | 22 | −73 | 6 | 68 | −86 | 6 | 34 | −43 | 71 | 34 |
| Average | −59 | 34 | 45 | −70 | 32 | 47 | −55 | −24 | 85 | −59 | 30 | 58 | −57 | 41 | 55 | −74 | 31 | 29 | −62 | 6 | 72 | −83 | 1 | 39 | −43 | 61 | 41 |
| Std dev | 2 | 2 | 1 | 9 | 4 | 6 | 10 | 20 | 7 | 8 | 16 | 10 | 8 | 13 | 9 | 6 | 13 | 10 | 11 | 15 | 7 | 8 | 15 | 9 | 9 | 19 | 8 |
| Distance | 10.71 | 0.00 | 68.93 | 15.39 | 17.21 | 19.07 | 36.33 | 34.75 | 39.80 | ||||||||||||||||||
Figure 4.
The dispersion of APB, ‘5‐cm method’, eDLPFCS and electrode positions are represented by spheroids in standardised space. Spheroids are centred at the mean position for each measurement with a radius in each direction (i.e. X, Y and Z) equal to 1 standard deviation. Please note that these positions were measured on the scalp so they are ‘flying’ over the grey matter.
Figure 3 compares the coordinates predicted by our method mDLPFCS with the position obtained with the co‐registration probe during the experiment, referred to as eDLPFCS in standardised space. A paired Hotelling's T‐squared test (SAS System v.9.1.3; SAS Institute, NC) was performed between the eDLPFCS and mDLPFCS and found that the locations differed significantly (T‐square = 46.44, df = 3,12, P = 0.0004). Furthermore, a series of paired t‐tests found the location of the mDLPFCS and eDLPFCS differed significantly in the x‐dimension (P = 0.0004), moderately in the y‐dimension (P = 0.0651), while there was no difference in the z‐dimension (P = 0.2947).
DISCUSSION
Here we presented a novel neuronavigational method to determine the most appropriate position to place the TMS coil on the scalp in order to target left DLPFC, and compared this with the ‘5‐cm method’ and ‘10‐20 method’. We found that our neuronavigational method was the least susceptible to inter‐subject variability followed by the ‘10‐20 method’ and lastly the ‘5‐cm method’ in standardised space. Furthermore, we found that our neuronavigational method yielded a DLPFC location more anterior and lateral than the ‘5‐cm method’ and between electrodes F3 and F5 of the ‘10‐20 method’. However, if MRI acquisition is not feasible, we recommend using the ‘10‐20 method’ by positioning the TMS coil over the F5 electrode as we found that the ‘10‐20 method’ was less susceptible to inter‐subject variability compared to the ‘5‐cm method’.
Consistent with Herwig et al. [ 2001], inter‐subject variability was found with the ‘5‐cm method’, which was greater than the variability found with our method (eDLPFCS position) and the ‘10‐20 method’ (Table III; Fig. 4). Also consistent with Herwig et al. [ 2001], we found that the ‘5‐cm method’ generated positions for the DLPFC that were posterior of our position for the DLPFC based on meta‐analyses on neuroimaging DLPFC activation during working memory in patients with depression and schizophrenia [Fitzgerald et al., 2006; Glahn et al., 2005; Mendrek et al., 2005; Tan et al., 2005]. Thus, the recommendations in this study are based on patients with depression and schizophrenia; however, the advantage of our neuronavigational method is that it can be employed to target any brain region.
The ‘10‐20 method’ was found to be less susceptible to inter‐subject variability compared to the ‘5‐cm method’ and yielded positions closer to the DLPFC position obtained by our method. Furthermore, when MRI coregistration is unavailable, the ‘10‐20 method’ should used to direct the TMS coil over the F5 electrode (Fig. 4; individual space). This finding, therefore, suggests that the TMS coil should be centred on electrode F5 and by extension F6 (‘10‐20 method’) to target the left and right DLPFC, respectively.
Our group has previously shown that targeting the DLPFC using neuronavigational techniques based using functional coordinates (x, y, z) = −45, 45, 35 (Talairach coordinates; (x, y, z) = −46, 45, 38; MNI coordinates) for this area results in a significant reduction in scores on the Montgomery‐Asberg Depression Rating Scale compared with those patients whose DLPFC was determined through the standard or ‘5‐cm method’ [Fitzgerald et al., 2009]. The functional coordinates investigated in this study were guided by a previous meta‐analysis on neuroimaging studies which examined working memory in patients with major depressive disorder (MDD; [Fitzgerald et al., 2006]). The results of the meta‐analysis found the DLPFC to be located within the juncture of BAs 9 and 46. Although, using this coordinate position indeed resulted in greater treatment efficacy, it does not preclude that other voxel coordinates within this juncture may more optimally improve the anti‐depressant effects of rTMS in MDD patients. In this regard, we selected our voxel coordinate for the DLPFC by first converting the coordinates used by Fitzgerald et al. [ 2009] to MNI coordinates that also were associated within the juncture of BAs 9 and 46. Our DLPFC coordinate resulted in a position that was a little more posterior and lateral to those examined by Fitzgerald et al. [ 2009]. In line with our position for the DLPFC, a recent study [Herbsman et al., 2009] who examined the relationship between the variability of the DLPFC location determined by the 5‐cm rule (i.e., ‘5‐cm method’) with scores on the Hamilton Depression Rating Scale in MDD patients. Herbsman et al. observed greater clinical response to rTMS in individuals with DLPFC positions that were more lateral and anterior compared to individuals with more medial and posterior locations. The mean position of the DLPFC was (x, y, z) = −46, 25, 44 (Talairach coordinates; (x, y, z) = −47, 24, 48; MNI coordinates) in those subjects with more lateral and anterior positions. The DLPFC position examined in this study (x, y, z) = −50, 30, 36; MNI coordinates) and the one in Herbsman et al. (x, y, z) = −47, 24, 48; MNI coordinates), thus, are more lateral and posterior to the coordinate previously investigated by our group [Fitzgerald et al., 2009], and suggests that a more lateral position within the junction of BAs 9 and 46 may more optimally improve treatment efficacy in MDD.
The results of this study are limited in several important ways. First, our proposed method for determining the position of DLPFCS assumes that the centre of the coil makes contact with the scalp in a single point therefore only one plane that was tangential to the scalp at this point was considered (see Fig. 3). However, hair and skin may have produced a different contact surface that may have caused a range of possible orientations for the TMS coil rather than a single tangential plane. This is consistent with the difference observed between the mDLPFCS and eDLPFCS locations in the x‐dimension, which may have arisen from Step 7 during the mDLPFCS voxel selection, which is manually selected. In this step the scalp DLPFC location in the MRI was delineated as an arbitrary value of colour intensity. A change in this threshold could move the scalp to a maximum in a voxel in either direction (1 voxel = 0.86 mm). The true difference observed in the x‐dimension between the two locations was equal to 10.4 mm in standardised space of which the size of the coregistration probe (8 mm), in addition to hair and skin may have contributed to this difference. The difference found between mDLPFC and eDLPFC positions, therefore, reflects a distance along the normal to the tangential plane that the TMS coil is positioned. Most importantly, regardless of which voxel for the mDLPFC we select along this line, the effect of the TMS on the DLPFC would not change and therefore is clinically insignificant. We have determined, however, that by selecting a voxel position that lies above the scalp rather than one that intersects the scalp, the difference arising in the x‐dimension will be minimised. For example, in Figure 2B we can superimpose a line representing the normal to the tangential plane on the scalp instead of a sphere. With this slight modification of our voxel selection process, any differences between the mDLPFC and eDLPFC positions would be owing to the variability in the MINIBIRD system itself. Second, since the non‐linear transformation (SPM) used in this study to convert the standard template to the individual brain (Fig. 1; Step 1) were designed to match the full brain rather than just the cortex, other transforms that are based on the trajectory of deep sulci in the cortex (i.e., surface‐based techniques for warping three‐dimensional images of the brain [Thompson and Toga, 1996]) may increase the accuracy of the method proposed in this study. Future studies examining the accuracy of using non‐linear transformations for determining the position of Talairach coordinates to individual cortex should be investigated. Furthermore, future studies should also aim to improve the algorithms used for rendering the surface of the scalp. Although the marching cubes algorithm (based on an arbitrary threshold value) seemed to work very well, this tends to render other iso‐surfaces (i.e., internal side of the skull and on the cortex) rather than just the iso‐surface of the subject's scalp. Removing these extra iso‐surfaces would decrease the filtering processes and possible bias involved when the voxel for the mDLPFCS is selected and therefore improve upon our method.
Although previous studies have also employed the marching cubes algorithm to determine scalp positions to target other brain regions [Andoh et al., in press], this is the first demonstration of neuronavigational methods which took into consideration the functional coordinates of the brain region of interest and the orientation of the TMS coil in order to optimally target the DLPFC. We used a novel neuronavigational method, which accurately targeted the DLPFC with less inter‐subject variability compared to both the ‘5‐cm method’ and ‘10‐20 method’. Our method improves upon these previous methods to localise the DLPFC in two respects. First, neuroimaging studies consistently report the location of the DLPFC at the juncture of BAs 9 and 46, however, our group previously demonstrated that using functional coordinates more accurately determines the most appropriate position in which to direct the TMS coil in order to optimise rTMS treatment efficacy in MDD [Fitzgerald et al., 2009]. Thus, we account for the fact that this is a functional brain region that is not considered in either the ‘5‐cm method’ or the ‘10‐20 method’. Second, a marching cubes algorithm determined the optimal location for TMS coil placement on the skull from the cortical position, thereby accounting for cortex morphology, skull shape, and the orientation of the TMS coil. Thus, we have minimised inter‐subject variability inherent in previous methods that do not consider characteristics of head and/or cortex or TMS coil orientation. The methods presented in this study, therefore, demonstrates a significant advancement to accurately target the DLPFC in rTMS treatment studies.
While the methods presented here require the addition of obtaining a T1‐weighted MRI, and involve several steps of neuronavigational processing that may be more expensive and time consuming compared to previous methods (e.g., the ‘5‐cm method’), a burgeoning treatment literature that was discussed previously [Fitzgerald et al., 2009] suggests that investing in such methods to optimise localisation and TMS targeting of the DLPFC is clinically superior to conventional treatment methods and should be pursued where possible. Our findings also suggest that in the event that MRI‐guided methods are not possible, placing the TMS coil over electrode F5 from the ‘10‐20 system’ should be used to target the left DLPFC.
Acknowledgements
The authors gratefully acknowledge the assistance of all persons and volunteers whose participation was essential in the successful completion of the study.
REFERENCES
- Andoh J, Riviere D, Mangin J, Artiges E, Cointepas Y, Grevent D, Paillere‐Martinot M, Martinot J, Cachia A ( 2009): A triangulation‐based magnetic resonance image‐guided method for transcranial magnetic stimulation coil positioning Brain Simulation. (in press). [DOI] [PubMed]
- Ashburner J, Friston KJ ( 1999): Nonlinear spatial normalization using basis functions. Hum Brain Mapp 7: 254–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner J, Neelin P, Collins DL, Evans A, Friston K ( 1997): Incorporating prior knowledge into image registration. Neuroimage 6: 344–352. [DOI] [PubMed] [Google Scholar]
- Evans AC, Collins DL ( 1993): A 305‐member MRI‐based sterotactic atlas for CBF activation studies. In: Proceedings of the 40th annual meeting of the Society for Nuclear Medicine.
- Fitzgerald PB, Oxley TJ, Laird AR, Kulkarni J, Egan GF, Daskalakis ZJ ( 2006): An analysis of functional neuroimaging studies of dorsolateral prefrontal cortical activity in depression. Psychiatry Res 148: 33–45. [DOI] [PubMed] [Google Scholar]
- Fitzgerald PB, Maller JJ, Hoy K, Thomson R, Daskalakis ZJ: Exploring the optimal site for the localization of dorsolateral prefrontal cortex in brain stimulation experiments (in press). [DOI] [PubMed]
- Fitzgerald PB, Hoy K, McQueen S, Maller JJ, Herring S, Segrave R, Bailey M, Been G, Kulkarni J, Daskalakis ZJ ( 2009): A randomized trial of rTMS targeted with MRI based neuro‐navigation in treatment‐resistant depression. Neuropsychopharmacology 34: 1255–1262. [DOI] [PubMed] [Google Scholar]
- George MS, Wassermann EM, Williams WA, Callahan A, Ketter TA, Basser P, Hallett M, Post RM ( 1995): Daily repetitive transcranial magnetic stimulation (rTMS) improves mood in depression. Neuroreport 6: 1853–1856. [DOI] [PubMed] [Google Scholar]
- Gerloff C, Corwell B, Chen R, Hallett M, Cohen LG ( 1997): Stimulation over the human supplementary motor area interferes with the organization of future elements in complex motor sequences. Brain 120 ( Part 9): 1587–1602. [DOI] [PubMed] [Google Scholar]
- Glahn DC, Ragland JD, Abramoff A, Barrett J, Laird AR, Bearden CE, Velligan DI ( 2005): Beyond hypofrontality: A quantitative meta‐analysis of functional neuroimaging studies of working memory in schizophrenia. Hum Brain Mapp 25: 60–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbsman T, Avery D, Ramsey D, Holtzheimer P, Wadjik C, Hardaway F, Haynor D, George MS, Nahas Z ( 2009): More lateral and anterior prefrontal coil location is associated with better repetitive transcranial magnetic stimulation antidepressant response. Biol Psychiatry. [DOI] [PubMed] [Google Scholar]
- Herwig U, Padberg F, Unger J, Spitzer M, Schonfeldt‐Lecuona C ( 2001): Transcranial magnetic stimulation in therapy studies: examination of the reliability of “standard” coil positioning by neuronavigation. Biol Psychiatry 50: 58–61. [DOI] [PubMed] [Google Scholar]
- Herwig U, Satrapi P, Schonfeldt‐Lecuona C ( 2003): Using the international 10–20 EEG system for positioning of transcranial magnetic stimulation. Brain Topogr 16: 95–99. [DOI] [PubMed] [Google Scholar]
- Jasper HH ( 1958): The ten‐twenty electrode system of the International Federation. Electroencephalogr Clin Neurophysiol 10: 370–375. [PubMed] [Google Scholar]
- Lorensen WE, Cline HE ( 1987): Marching Cubes: A high resolution 3D surface construction algorithm. Proceedings of SIGGRAPH 21, 163–169. [Google Scholar]
- Mazziotta J, Toga A, Evans A, Fox P, Lancaster J, Zilles K, Woods R, Paus T, Simpson G, Pike B, et al. ( 2001): A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM). Philos Trans R Soc Lond B Biol Sci 356: 1293–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendrek A, Kiehl KA, Smith AM, Irwin D, Forster BB, Liddle PF ( 2005): Dysfunction of a distributed neural circuitry in schizophrenia patients during a working‐memory performance. Psychol Med 35: 187–196. [DOI] [PubMed] [Google Scholar]
- Pascual‐Leone A, Rubio B, Pallardo F, Catala MD ( 1996): Rapid‐rate transcranial magnetic stimulation of left dorsolateral prefrontal cortex in drug‐resistant depression. Lancet 348: 233–237. [DOI] [PubMed] [Google Scholar]
- Rossi S, Cappa SF, Babiloni C, Pasqualetti P, Miniussi C, Carducci F, et al. ( 2001): Prefrontal [correction of Prefontal] cortex in long‐term memory: An “interference” approach using magnetic stimulation. Nat Neurosci 4: 948–952. [DOI] [PubMed] [Google Scholar]
- Tan HY, Choo WC, Fones CS, Chee MW ( 2005): fMRI study of maintenance and manipulation processes within working memory in first‐episode schizophrenia. Am J Psychiatry 162: 1849–1858. [DOI] [PubMed] [Google Scholar]
- Thompson P, Toga AW ( 1996): A surface‐based technique for warping three‐dimensional images of the brain. IEEE Trans Med Imaging 15: 402–417. [DOI] [PubMed] [Google Scholar]