Abstract
Purpose:
To improve the accuracy of quantitative susceptibility mapping plus quantitative blood oxygen level-dependent magnitude (QSM+qBOLD or QQ) based mapping of the oxygen extraction fraction (OEF) and cerebral metabolic rate of oxygen (CMRO2) using cluster analysis of time evolution (CAT).
Methods:
3D multi-echo gradient echo and arterial spin labeling images were acquired in 11 healthy subjects and 5 ischemic stroke patients. Diffusion Weighted Imaging (DWI) was also performed in patients. CAT was developed for analyzing signal evolution over echo time. QQ-based OEF and CMRO2 were reconstructed with and without CAT, and results were compared using ROI analysis and a paired t-test.
Results:
Simulations demonstrated that CAT substantially reduced noise error in QQ-based OEF. In healthy subjects, QQ-based OEF appeared less noisy and more uniform with CAT than without CAT; average OEF with and without CAT in cortical gray matter was 32.7 ± 4.0 and 37.9 ± 4.5 %, with corresponding CMRO2 of 148.4 ± 23.8 and 171.4 ± 22.4 μmol/100g/min, respectively. In patients, regions of low OEF were confined within the ischemic lesions defined on DWI when using CAT, which was not observed without CAT.
Conclusion:
The cluster analysis of time evolution (CAT) significantly improves the robustness of QQ-based OEF against noise.
Keywords: cerebral metabolic rate of oxygen, oxygen extraction fraction, quantitative susceptibility mapping, quantitative blood oxygenation level-dependent imaging, machine learning, K-means, cluster analysis of time evolution
INTRODUCTION
The cerebral metabolic rate of oxygen (CMRO2) and oxygen extraction fraction (OEF) are important markers of brain tissue viability and function, such as in stroke (1–3), and their mapping using MRI has received great interest (4). Quantitative models have been proposed to investigate the effect of deoxyhemoglobin in blood, a strong paramagnetic source, on the MRI signal, including 1) magnitude signal modeling methods such as quantitative imaging of extraction of oxygen and tissue consumption (QUIXOTIC) (5), calibrated fMRI (6–9), and quantitative BOLD (qBOLD) (10–12), and 2) phase signal modeling methods for a value of the whole brain CMRO2 (13–16) and a voxel-wise quantitative susceptibility mapping (QSM)-based CMRO2 methods (17–19).
Recently, QSM and qBOLD (QSM+qBOLD=QQ) have been combined to model the effect of OEF on the magnitude and phase of multi-echo gradient echo (mGRE) data (20). This QQ approach enables OEF and CMRO2 mapping without vascular challenges that are difficult to administer in clinic practice. However, QQ remains challenging, because qBOLD with a strong coupling between venous oxygenation (Y) and venous blood volume () is very difficult to invert (11). The qBOLD inversion is highly sensitive to noise, susceptible to substantial errors in OEF at typical signal-to-noise (SNR) levels (11,21).
We introduce here a cluster analysis of time evolution (CAT) method to overcome the noise sensitivity of QQ-based OEF by improving the effective SNR. The basic idea of the CAT method is that voxels with a similar mGRE signal evolution have similar model parameter values and that the number of clusters as determined by machine learning is much smaller than the number of voxels. Consequently, averaging over a cluster can substantially increase SNR for a cluster-wise inverse solution that can be used as a robust initial guess for voxel-wise QQ optimization. In this study, QQ-based OEF and CMRO2 with and without CAT (20) were compared in simulations, healthy subjects and ischemic stroke patients.
THEORY
CMRO2 (μmol/100g/min) and OEF (%) can be expressed as
| [1] |
| [2] |
where CBF is the cerebral blood flow (ml/100g/min), [H]a=7.377μmol/ml is the oxygenated heme molar concentration in the arteriole based on a hematocrit of Hct=0.357 (18), Y the venous oxygenation (dimensionless), and Ya = 0.98 the arterial oxygenation, where [H] is 7.53 μmol/ml is the heme molar concentration with Hct=0.357 (17). The qBOLD method models the mGRE magnitude in a voxel as (20):
| [3] |
where G(t) is the macroscopic field effect at time t (20), FBOLD is the deoxygenated blood effect inside the voxel: FBOLD(Y, v, χnb, t) = exp[-v ⋅ fs(δω ⋅ t)] (11), where fs is the signal decay by the blood vessel network (12), and δω is the characteristic frequency due to the susceptibility difference between deoxygenated blood and the surrounding tissue (20):
| [4] |
with γ=267.513MHz/T the gyromagnetic ratio, B0 the main magnetic field, Δχ0 = 4π × 0.27ppm the susceptibility difference between fully oxygenated and fully deoxygenated red blood cells (22), χba = −108.3 ppb the susceptibility of fully oxygenated blood, using the assumed Hct above (19), and χnb is the susceptibility of non-blood materials in tissue.
Due to the non-linear nature of Eq. 3, qBOLD based OEF estimates are highly dependent on initialization and SNR (21). To increase the effective SNR, we propose a novel Cluster Analysis of Time evolution (CAT) method for QSM+qBOLD (“QQ with CAT” hereafter). This method is based on the following insights. Voxels with similar signal time-course SqBOLD(t)/G(t) have similar tissue parameters (Y, v, R2). Many voxels have very similar signal time-courses and form a cluster for an effective signal averaging or SNR improvement (23). K-means clustering can be used to identify these clusters (24). The QQ problem is solved first with a cluster-wise optimization by assuming parameters Y, v, and R2 to be constant within each cluster while S0 and χnb are allowed to vary from voxel to voxel, since the magnitude and phase signals depend predominantly on S0 and χnb, respectively. Next, a voxel-wise optimization is performed by using the solution from the cluster-wise optimization as the initial guess.
QQ is formulated as:
| [5] |
where w is the weighting on the QSM term, and
| [6] |
with χ the measured susceptibility, χba = ψHb ⋅ χoHb + (1 − ψHb) ⋅ χp the fully oxygenated blood susceptibility (19), α = 0.77 the ratio between the venous and total blood volume v/CBV (25), ψHb = 0.0909 the hemoglobin volume fraction assuming Hct =0.357 (18,26–28), χp = −37.7 ppb the blood plasma susceptibility (29), ΔχHb = 12522 the susceptibility difference between deoxy- and oxyhemoglobin (17,29). The third term in Eq. 5 used the physiological constraint that the OEF averaged over the brain, , should be similar to OEFwb, the brain OEF value estimated from the main draining vein, the straight sinus: OEFwb = Hctvt ⋅ OEFss where Hctvt = 0.759 is the hematocrit ratio between large vessels (26) and brain tissue, and with estimated from the average susceptibility in the straight sinus with ψHb = 0.1197 (20,27,28), v = 1 and χnb = 0 in Eq. 6. In Eq. 5, S(t) is the measured mGRE data, and λ the regularization strength.
METHODS
Numerical Simulation 1
To investigate the relationship between SNR and the dependency of OEF on the initial guess, we performed a simulation. The mGRE and susceptibility values were simulated using Eqs. 3 and 6, respectively. The input (ground truth) was Y = 60%, χnb = −0.1 ppm, S0 = 1000 au, and R2 = 20 Hz. For the v input, two v values were used: 3% (Case 1) and 1% (Case 2). The same echo times are used as in the healthy subjects (TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms). Gaussian noise was added to the mGRE signals and the QSM values to obtain SNR ∞ (no noise), 1000, 100, and 50. For each SNR, the optimization was subsequently performed to estimate Y with different initial guesses for Y(0.15,0.3,0.45,0.6,0.75,0.9) and v (0.01,0.03,0.05,0.07). The ground truth was used for the initial guesses of S0, χnb and R2. This was repeated for 500 times for each SNR. w=5 × 10−3 and λ = 0. A relative error was computed as .
Numerical Simulation 2
To compare the accuracy of QQ with and without CAT (20), we performed a simulation. First, the mGRE signals and the QSM values for each brain voxel were simulated using Eqs. 3 and 6, respectively, using the same echo times as in the stroke patients (see below). The input (ground truth) was the result from QQ with CAT method in one stroke patient, who was imaged 6 days post onset (see below). The average OEF and v across the brain was 29% and 0.97%, respectively. Gaussian noise was added to the mGRE signals and the QSM values to obtain SNR ∞ (no noise), 1000, 100, and 50. For each SNR, the simulated data was processed in two ways: 1) QQ without CAT, with a constant OEF initial guess for the whole brain (20) and 2) QQ with CAT. The same optimization, including w = 5 × 10−3 and λ = 103, was performed as in experimental data (see below). OEFwb was set to the average ground truth OEF across the brain (29 %). Root-mean-square error (RMSE) was calculated to measure accuracy.
Data Acquisition
Healthy subjects:
This study was approved by the local Institutional Review Board. Healthy volunteers were recruited (n=11; 10 males, 1 female, mean age 34 ± 12 years) for brain MRI on a 3T scanner (HDxt, GE Healthcare) using an 8-channel brain receiver coil. After obtaining consent, all subjects were instructed to avoid caffeine or alcohol intake 24 hours prior to the MRI. MRI was performed in the resting state (15) using a 3D fast spin echo (FSE) arterial spin labeling (ASL) sequence (31–33), a 3D spoiled mGRE sequence (13,34,35), and an inversion prepared T1w SPGR sequence (BRAVO) (36). The 3D FSE ASL sequence parameters were: 20 cm FOV, 1.56 mm in-plane resolution, 3.5 mm slice thickness, 1500 ms labeling period, 1525 ms post-label delay, 976.6 Hz/pixel bandwidth, spiral sampling of 8 interleaves with 512 readout points per leaf, 35 axial slices, TE=10.1 ms, TR=4533 ms, and 3 signal averages. The 3D mGRE sequence parameters were: 0.78 mm in-plane resolution, 1.2 mm slice thickness, volume coverage identical to the 3D FSE ASL sequence, 7 equally spaced echoes: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms, TR= 30.5 ms, bandwidth 488.3 Hz/pixel and flip angle 15o. The pulse sequence was flow-compensated in all three directions (34). The inversion prepared T1w SPGR sequence parameters were: 0.78 mm in-plane resolution, 1.2 mm slice thickness, volume coverage identical to the 3D FSE ASL sequence, TE=2.92ms, TR=7.69 ms, 450 ms prep time, bandwidth 195.2 Hz/pixel, and flip angle 15o (Supporting Information Table S1a).
Stroke patients:
MRI was performed in 5 ischemic stroke patients using 3D ASL, 3D mGRE, and DWI on a clinical 3T scanner (GE MR Discovery 750) using a 32-channel brain receiver coil. The time interval between stroke onset and MRI examination ranged between 6 hours and 12 days. All lesions were located in unilateral cerebral artery territory. The 3D FSE ASL sequence parameters were: 24 cm FOV, 1.9 mm in-plane resolution, 2.0mm slice thickness, 1500 ms labeling period, 1525 ms post-label delay, 976.6 Hz/pixel bandwidth, 68 axial slices, TE=14.6 ms, TR=4787 ms, and 3 signal averages. The 3D mGRE sequence parameters were: 0.47mm in-plane resolution, 2mm slice thickness, volume coverage identical to the 3D FSE ASL sequence, 8 equally spaced echoes: TE1/ΔTE/TE8 = 4.5/5/39.5 ms, TR= 42.8 ms, bandwidth=244.1 Hz/pixel, and flip angle 20o. DWI sequence parameters were: 24 cm FOV, 0.94 mm in-plane resolution, 3.2 mm slice thickness, 1953.1 Hz/pixel bandwidth, 0, 1000 s/mm2 b-values, TE=71 ms, TR=3000 ms, and 4 signal averages (Supporting Information Table S1b).
Image Processing
Healthy subjects:
QSM reconstruction was performed as follows: first, an adaptive quadratic-fit of the mGRE phase was performed to estimate the total field (30). Second, the Projection onto dipole fields (PDF) method was used to obtain the local field (31). Finally, the Morphology Enabled Dipole Inversion with automatic uniform cerebrospinal fluid zero reference (MEDI+0) algorithm was used to compute susceptibility (32–35). CBF maps (ml/100g/min) were generated from the ASL data using FuncTool (GE Healthcare, Waukesha, WI, USA). All images were co-registered and interpolated to the resolution of the QSM maps using the FSL FLIRT algorithm (36,37).
Stroke patients:
QSM and CBF processing was the same as in the healthy subjects, except a linear-fit of the mGRE phase was used to estimate the total field as 3D flow-compensation was not available on the scanner used in the patient studies.
Clustering
The mGRE magnitude signal S(t) was used for clustering after the macroscopic field inhomogeneity contribution, G was removed (See appendix of (38)). For the purpose of clustering, the mGRE signal for each voxel was normalized by the average signal across echoes. The K-means clustering algorithm using the squared Euclidean distance (39–42) was then applied to cluster voxels with similar normalized signal evolution across echoes. Conventional K-means clustering requires an a priori choice of the number of clusters, denoted by K. Here, we used the X-means method (43) that automatically selects K. In this method, two operations are repeated iteratively. In Step 1, a conventional K-means clustering with a given initial number of clusters is performed and the Bayesian Information Criterion (BIC) measure is computed (44), which is the sum of the clustering log-likelihood and a penalty on K. As K increases, goodness of fitting (log-likelihood) increases, but the possibility of overfitting also increases. The penalty term on K reduces this possibility. In Step 2, the centroid (the center of mass) for each cluster is replaced by two child centroids, and a local K-means (K = 2) is performed within that cluster using those child centroids as initial guesses. In order to decide whether each cluster should be replaced by the two obtained child clusters, the BIC is computed for this cluster: a larger BIC indicates a replacement is desired, otherwise the ‘parent’ centroid is kept. Steps 1 and 2 are repeated until the overall BIC stops increasing or until K reaches an a priori set maximum. In this study, 1 and 50 was used for the initial and maximum number of clusters, respectively.
For speed, the X-means algorithm to obtain the optimal number of clusters K was carried out on 10% of the total voxels, randomly selected. This process was repeated 10 times and the K with the largest BIC value among the 10 trials was selected. The corresponding centroids were then used as the initial centroids for the final K-means on all voxels.
Optimization
The QSM+qBOLD (QQ) optimization (Eq.5) was solved by iteratively solving the following subproblems: 1) updating S0 based on qBOLD (Eq. 7); 2) updating χnb based on QQ optimization (Eq. 8) χ, and 3) updating the Y, v, R2 values based on QQ optimization (Eq. 9). Concretely, in the kth step, the subproblems are:
| [7] |
| [8] |
| [9] |
Eq. 7 was solved using closed form expressions, while Eqs. 8 and 9 were solved iteratively. First, Y, v, R2 were initialized as follows: Y0 was estimated from OEFwb in Eq. 5. The straight sinus mask was obtained automatically using global and regional thresholding on QSM combined with positional (inferior, posterior brain) and geometrical (straightness of the vein) constraints. For initial guesses for v (v0), the whole brain was roughly segmented into three parts, gray matter (GM), white matter (WM), and cerebral spinal fluid (CSF) with either T1w (11 healthy subjects and 4 stroke patients) or T2-FLAIR image (1 stroke patient without T1w image) via FSL FAST (45). v0 was set to 3/1.5/1% for GM/WM/CSF, respectively based on literature (10,11). χnb,0 was set to satisfy Eq. 6 with Y0 and v0. The initial guess S0,0 and R2,0 were obtained by solving Eq. 3, and using Y0, v0 and χnb,0. The resulting mono-exponential fit was performed using ARLO (46). Before fitting, 3D Gaussian smoothing (standard deviation of 0.5 of the diagonal length of the voxel) was performed on S and G to improve SNR. Voxels with R2 >100 Hz or R2 < 2.5 Hz were considered as outliers and removed from all subsequent processing.
Second, using the resultant clusters obtained in the Clustering section, a cluster-based optimization was performed, in which the unknowns Y, v, R2 were assumed to be constant within each cluster. The average of the Y0, v0, R2,0 across each cluster was used as the initial value for that cluster. To improve convergence behavior during non-linear fitting, the unknows Y, v, χnb, R2 were scaled to have roughly the same order of magnitude: , where x is the unknown in the original scale, c is the scaling factor: 0.5, 0.05, |χnb,0|, avg(R2,0) + 4. SD(R2,0) for Y, v, χnb, R2, respectively. avg(R2,0) and SD(R2,0) denote the average and standard deviation of R2,0 in the cluster, respectively. Lower and upper bounds were set to 0.0 and 0.98 for Y (before scaling), 0.4v0 and 2v0 for v (before scaling), 0.5 and 1.5 for R2 (after scaling). For χnb, the lower and upper bounds were set to the value χnb calculated from Eq. 6 with Y/v/=0.98/0.1 and 0.0/0.1, respectively. The optimization was performed on all clusters jointly. To compensate for the scale of the input MRI data, the qBOLD term in Eq. 8 and 9 was normalized by where is the average of the magnitude of the first echo across the whole brain, Nvoxel the number of voxels, and NTE the number of echoes. The QSM term in Eq. 8 and 9 was also normalized by . The regularization weighting factor (λ) and the weighting on the QSM (w) were chosen by performing L-curve analysis (47): λ was first chosen with w = 0, then w was chosen with the previously decided λ. The limited-memory Broyden-Fletcher-Goldfarb-Shanno-Bound (L-BFGS-B) algorithm was used for the constrained optimization (48,49). The optimization was stopped when the relative residual , with Ek,n the energy of the kth iteration at the kth step, was smaller than 10−5 for Eqs. 8 and 9. For the kth step, the optimization was stopped when with nk the number of L-BFGS-B iterations at step k after convergence. To prevent L-BFGS-B from not updating the Hessian when the residual falls below a preset threshold, the cost function was multiplied by a factor of 104 before L-BFGS-B was started.
Third, voxel-wise QQ optimization was performed using L-BFGS-B, allowing Y, v, and R2 to vary from voxel to voxel. The cluster-based result was used as initial guess. The scaling was the same as the cluster-wise optimization. The lower and upper bounds were set to 0.7 and 1.3 of the initial guesses. The optimization was stopped when rk,n < 2 × 10−4 for Eqs 8 and 9, and ρk < 10−2.
For Numerical Simulation 1, the same optimization settings were used as for experimental data, except for the fixed lower and upper bounds for v, 0.01 and 0.1 before scaling.
QQ with CAT method was compared with QQ without CAT, which uses a constant initial guess OEF for the whole brain (20). For QQ without CAT, we followed the optimization described in (20). The weight on QSM (w) was set to 100 for healthy subjects and stroke patients based on L-curve analysis. The optimization was stopped when the relative residual was smaller than 0.005 for healthy subjects and 0.001 for the stroke patients.
All algorithms were implemented in Matlab R2016a (Mathworks Inc., Natick, MA). All the clustering and optimization were carried out with an Intel Core i7–6900K 3.2 GHz processor. The computation time of the clustering, cluster-wise and voxel-wise optimization were 2.7 ± 0.7 mins, 3.3 ± 0.7 mins, and 4.6 ± 1.1 mins respectively for the 11 healthy subjects (106 voxels and 7 echoes), and 8.8 ± 2.5 mins, 8.8 ± 1.6 mins, 7.6 ± 1.2 mins respectively for the 5 stroke patients (1.8×106 voxels and 8 echoes). The code used for the experiments in this work, upon this paper publication, will become available for download from https://med.cornell.edu/mri.
Statistical Analysis
ROI analyses (mean and standard deviation) and paired t-tests were performed to compare CMRO2 and OEF values between QQ with and without CAT. For the ROIs in the healthy subjects, cortical gray matter (CGM) masks were constructed based on T1-weighted images by an experienced neuroradiologist (S.Z. 7 years of experience). For the stroke patients, ROIs for the lesion and its corresponding contralateral side were drawn based on DWI by the same neuroradiologist. To investigate the dependency on the number of clusters, conventional K-means was performed with K=1,5,10,15, 20, and the X-means result. QQ with CAT was subsequently performed for each K. The same optimization scheme was used as in experimental data including w/λ = 5 × 10−3/103. To investigate the OEF difference among different K values, a repeated measures ANOVA was performed.
RESULTS
In the optimal number of clusters determined by X-means, the difference between the 10% sub-sampling scheme and 100% sampling was on average <1 in 11 healthy subjects and 5 stroke patients (N=16). The 10% sub-sampling scheme (including the 10 trials) was 5~10 times faster than 100% sampling. The optimal number of clusters by the X-means method was 10 ± 2 in healthy subjects (N=11) and 16 ± 0 in stroke patients (N=5).
In the L-curve analysis, the corners for 4 randomly chosen subjects (2 healthy subjects and 2 stroke patients) were located at λ = 103 and w = 5 × 10−3. Figure 1 shows the influence of SNR on the sensitivity of the estimated Y on the initial guess (Numerical Simulation 1). Without noise, the relative error was low, but as SNR decreased from 1000 to 50, the relative error tended to increase when the initial guess deviated from the ground truth. For instance, at SNR 50 in Case 1, the relative error was 7.5% when Y0 = 0.6 and v0 0.03, but it was 29.1 % when Y0 = 0.15 and v0 = 0.03.
Figure 1.
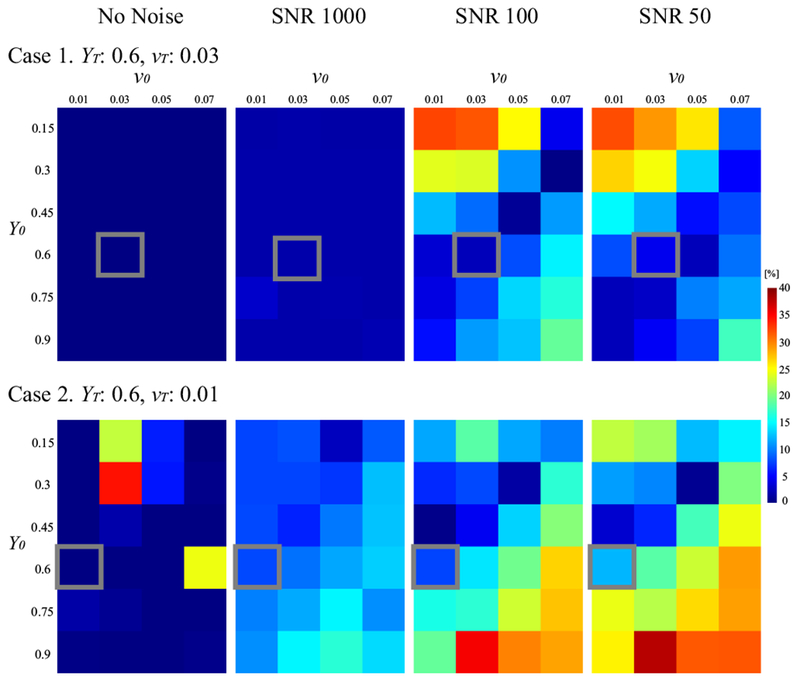
Influence of SNR on the sensitivity of the estimated Y on the initial guess (Numerical Simulation 1). Shown is the relative error between the estimated Y and the ground truth (YT). Y0 and v0 are the initial guesses of Y and v, respectively. As SNR decreases, Y becomes increasingly more sensitive to the initial guess, resulting in larger errors when the initial guess is away from the ground truth value. This seems more severe in the case with smaller v: vT = 0.03 (Case 1) vs. 0.01 (Case 2). The gray box indicates the ground truth values (YT and vT).
Figure 2 shows the comparison of the OEF maps obtained using QQ with and without CAT in the simulated stroke brain (Numerical Simulation 2). QQ with CAT provided a more accurate OEF map than that without CAT, especially at low SNRs. For instance, at SNR 50, QQ with CAT captured the low OEF region, whereas QQ without CAT did not accurately depict low OEF values. QQ with CAT provided lower RMSE than QQ without CAT for all SNRs.
Figure 2.
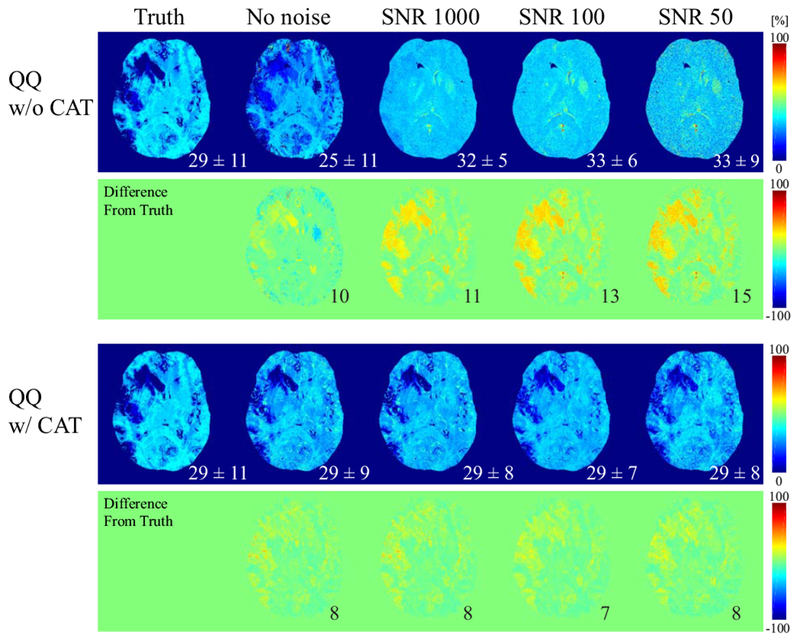
Comparison between the OEF obtained by QQ without and with CAT at different SNRs in the simulated stroke brain (Numerical Simulation 2). At all SNRs, QQ with CAT captures low OEF values, whereas QQ without CAT is not sensitive to low OEF values at low SNRs. The numbers in white indicate the OEF average and standard deviation in the whole brain, and black represents the root-mean-square error (RMSE).
Figure 3 shows a comparison between QQ with and without CAT in a healthy subject. The OEF with CAT appeared less noisy and more uniform, whereas OEF without CAT was noisy and had extreme values, for example >80% in deep gray matters. QQ with CAT showed a good CMRO2 contrast between CGM and WM without extreme values seen in QQ without CAT. v showed CGM/WM contrast and generally had lower values than QQ without CAT.
Figure 3.
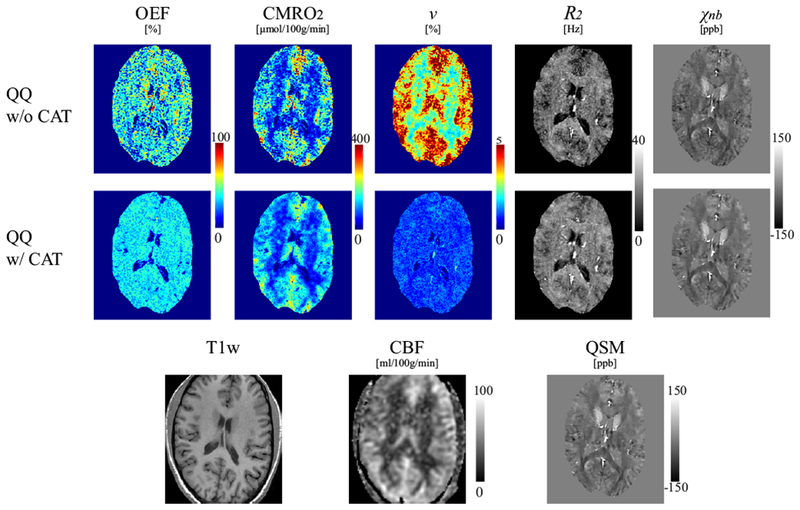
Comparison of OEF, CMRO2, v, R2 and χnb maps between QQ without and with CAT in a healthy subject. QQ with CAT shows a less noisy and more uniform OEF, and a good CMRO2 contrast between cortical gray matter and white matter without extreme values. The corresponding anatomy as depicted on a T1-weighted image, CBF map and susceptibility map are shown for reference.
Figure 4 shows the OEF, CMRO2, v, R2, and χn,b maps in one stroke patient (6 days post stroke onset) using QQ with and without CAT. In the OEF and CMRO2 maps, the lesion was distinguished more clearly using QQ with CAT than without. A low OEF region was clearly contained within the lesion as defined on DWI. However, QQ without CAT did not show a clearly localized low OEF region, neither within nor outside of the DWI-defined lesion. QQ with CAT generally showed low v regions specific to the DWI defined lesion, while QQ without CAT showed similar v contrast to that of CBF. QQ with CAT generally had higher R2 and χnb.
Figure 4.
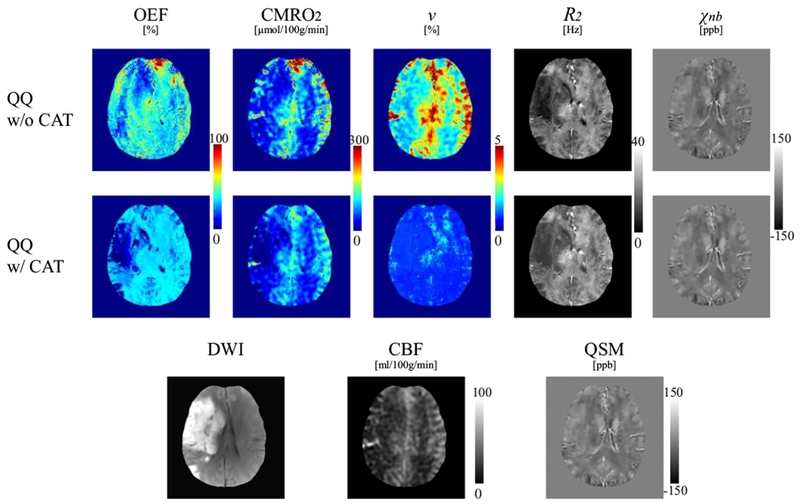
Comparison of OEF, CMRO2, v, R2 and χnb maps between QQ without and with CAT in a stroke patient imaged 6 days post stroke onset. In the CMRO2 and OEF maps, the lesion can be distinguished more clearly with QQ with CAT. For QQ with CAT, a low OEF region is clearly visualized and contained with the lesion region as defined on DWI, but a low OEF region obtained with QQ without CAT is not as well localized nor contained within the lesion as defined on DWI. QQ with CAT generally shows lower v in the DWI-defined lesion. The contrast in v in QQ without CAT result is similar in appearance to that of CBF. QQ with CAT shows generally higher R2 and χnb maps.
Figure 5 shows an OEF histogram in the lesion and in its contralateral region for both QQ with and without CAT in a second stroke patient (12 days post stroke onset). The OEF with CAT was distributed differently in the lesion as compared to the contralateral side. The lesion showed 8 peaks with the strongest two peaks at 0 and 17.5%, while the contralateral side had 6 peaks with dominant peaks at 35 ~ 45%. However, QQ without CAT did not have a distribution specific to low OEF values in the lesion, but there were bell-shaped distributions for both the lesion and contralateral side (broader in the contralateral side) with peaks at 47% and 49%, respectively.
Figure 5.
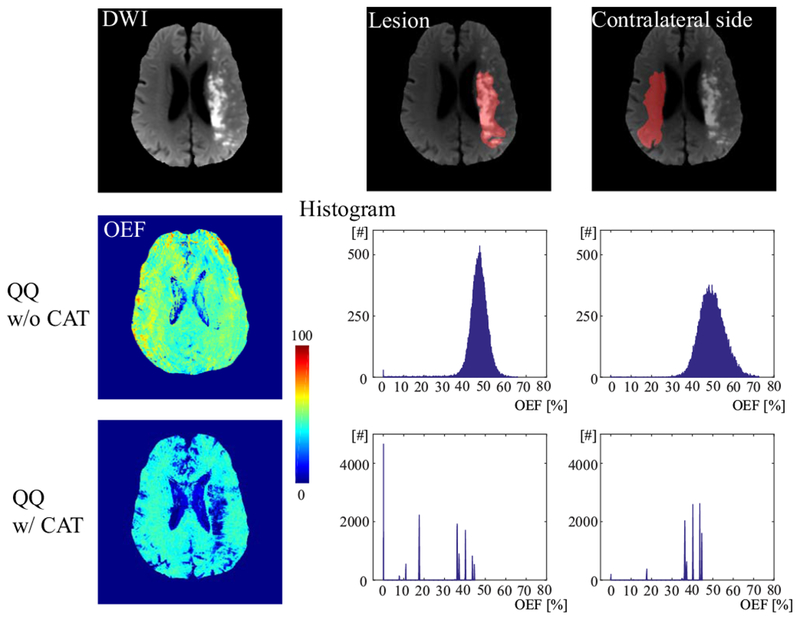
The histogram of OEF values in the lesion and its contralateral side in a second stroke patient imaged 12 days post stroke onset. QQ with CAT shows a different distribution in the lesion as compared to mirror side. The lesion shows 8 peaks with the strongest two peaks at 0 and 17.5%, while the contralateral side has 6 peaks with dominant peaks at 35 ~ 45%. However, QQ without CAT does not have a distribution specific to low OEF values in the lesion, but there are bell-shaped distributions for both the lesion and contralateral side (broader in the contralateral side) with peaks at 47% and 49%, respectively.
Figure 6 shows the segmentations and resulting OEF maps for a range of cluster numbers in the third stroke patient (4 days post stroke onset). The resultant OEF maps had a similar appearance for all K larger than 5, and were not significantly different: p=0.9999, F(5, 8520050)=0.0164 (repeated measures ANOVA). The X-means selected K = 17. The same pattern was observed in a healthy subject (Supporting Information Figure S1)
Figure 6.
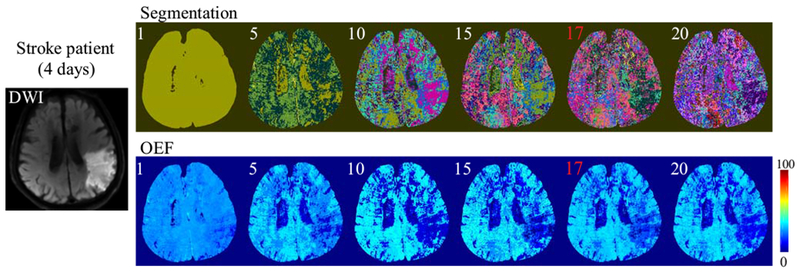
The segmentations and resultant OEF maps using a different number of clusters (K = 1,5,10,15,20, as well as the X-means result, 17 indicated in red) in a third stroke patient (4 days post stroke onset). In the segmentations, different colors indicate different clusters. The resulting OEF appearance is nearly constant for K ≥ 5.
Figure 7 shows the X-means clusering result (K = 17) and the average signal evolution for each clusters in the third stroke patient (4 days post stroke onset). The lesion and the contralateral side had distintively different dominant clusters: green clusters in the lesion and blue and pink clusters in the contralateral side. The corresponding average signal evolution was also different between the lesion and contralateral side.
Figure 7.
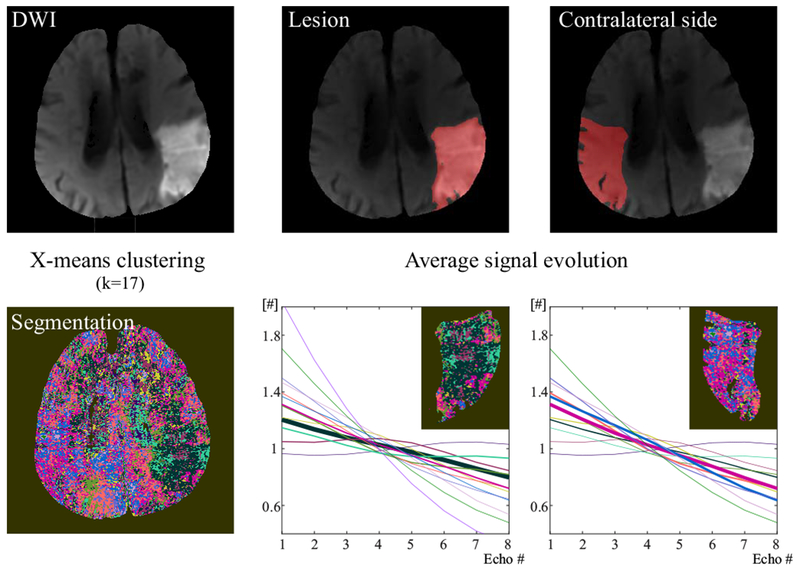
X-means clusering (K = 17) and the average signal evolution for each clusters in the third stroke patient (4 days post stroke onset). Different color indicates different cluster in the segmentation map. The corresponding average sigal evolution was shown in the same color as the cluster color. The width of the signal evolution is proportional to the number of voxels within clusters in the lesion and the contralateral side: The thicker the curve is, the more voxels the correspoding cluster has. For each voxel, the signal evolution was normalized by the average signal across echoes after the macroscopic field inhomogeneity contribution, G was removed. The average of these normalized signal evolutions across each cluster is shown here in different colors.
Figure 8 shows the ROI analysis in the CGM of healthy subjects using QQ with and without CAT. QQ with CAT showed smaller OEF, CMRO2 and v than QQ without CAT (N=11,): OEF was 32.7 ± 4.0 % and 37.9 ± 3.1 % (p<0.01), CMRO2 was 148.4 ± 23.8 and 171.4 ± 22.4 μmol/100g/min (p<0.01), v was 1.00 ± 0.2 % and 4.45 ± 0.39 % (p<0.01). Meanwhile, QQ with CAT showed higher R2 and χnb values than QQ without CAT: R2 was 16.5 ± 0.5 Hz and 13.1 ± 0.7 Hz (p<0.01), χnb is −20.2 ± 8.1 ppb and −33.8 ± 9.0 ppb (p<0.01).
Figure 8.
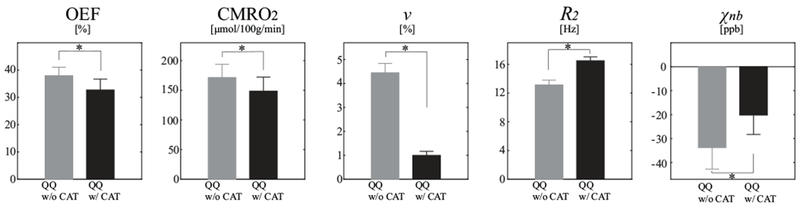
Average and standard deviation of OEF, CMRO2, v, R2, and χnb maps between QQ without and with CAT in cortical gray matter from healthy subjects (N=11). QQ with CAT shows smaller average CMRO2, OEF and v than the one without CAT, but QQ with CAT shows higher average R2 and χnb values. * p<0.01 (paired t-test).
DISCUSSION
Our results indicate that the cluster analysis of time evolution (CAT) substantially improves the robustness against noise of QSM+qBOLD (QQ) based mapping of OEF and CMRO2. Compared to QQ without CAT, the denoised OEF map demonstrates greater accuracy in simulations, appears more uniform in healthy subjects, and depicts a spatial pattern of low values within the DWI-defined ischemic lesions in stroke patients. Therefore, the CAT enables robust QQ-based OEF mapping from mGRE data alone without vascular challenges.
Clustering is an effective tool for dealing with noise in time-series data, as demonstrated in fMRI where the signal change is a very small percentage and very noisy (50,51). The echo-time series data of mGRE is stronger than fMRI time series. However, the QQ model is fundamentally relying on the separation of deoxyheme in cylindrical geometries from other susceptibility sources diffusely distributed in tissue. Use of two field strengths may also help separation of superparamagnetic ferritin from paramagnetic deoxyheme (52), but this is impractical in a clinical setting. The difference between echo time-series of random cylinders and diffuse distribution in qBOLD is about 10% (12,53), which is stronger than the signal change in fMRI but fundamentally makes QQ inversion sensitive to noise. Clustering as in CAT promises to allow robust QQ-based OEF and CMRO2 mapping in clinical practice.
Compared to QQ without CAT, OEF maps obtained using the proposed CAT method are more uniform and have less extreme values in healthy subjects (Figure 3), in agreement with previous PET studies (54,55). The suppressed noise is likely due to the use of cluster-wise optimization. Unknowns are assumed to be constant throughout the cluster, thereby creating an effective signal averaging. The simulations suggest that the resulting higher SNR makes the estimated parameters less sensitive to measurement noise. The overall noise reduction in Y and v also propagates into χnb and R2 maps with noise reduction benefits, compared to QQ without CAT (Figure 3).
QQ with CAT shows smaller OEF values (Figure 3 and 8), e.g. 32.7 ± 4.0 % and 37.9 ± 3.1 % (p<0.01) in CGM for QQ with and without CAT, respectively. The smaller OEF values in QQ with CAT are accompanied by higher R2, as compared to the one without CAT (16.5 ± 0.5 Hz vs.13.1 ± 0.7 Hz). This can be explained by that for the same measured magnitude signal decay, OEF decreases if R2 increases (Eq. 3 and 4). Both OEF values with and without CAT fall within the range previously reported for OEF obtained using PET: 35 ± 7 % (56) and 40 ± 9 % (55), and with other MRI based techniques: 26 ± 2 % (5), 31.7 ± 6.1 % (57), 35 ± 4 % (7), and 38 ± 14% (6).
QQ with CAT shows smaller v values in healthy subjects than QQ without CAT: 1.00 ± 0.2 % vs 4.45 ± 0.39 (p<0.01) in CGM. Compared to PET and other MR techniques, the v from QQ with and without CAT is a bit smaller and larger, respectively: the v values obtained using PET, e.g. 1.9 ± 0.5 % (58) and 2.0 ± 0.2 % (59), and other MR techniques: 1.75 ± 0.13 % (10), 1.9 ± 0.5 2.46 ± 0.28 (25), 2.68 ± 0.47 % (60), 3.6 ± 0.4% (61). Further studies are needed to investigate the cause of the lower v from QQ with CAT than literature, e.g. performing an experiment that the v truth is known. It is because the ground truth v has not been measured directly and different v estimation methods have their own assumptions to be verified (62). For instance, qBOLD methods set the non-blood tissue susceptibility (χnb) to be uniform in the whole brain with the fully oxygenated blood susceptibility equal to −108 ppb (10,60), however tissue iron and myelin would cause regional χnb variation. The gray matter χnb value in this study, −20.2 ppb, was higher than the χnb value assumed in qBOLD. The inclusion of QSM in QQ with the greater χnb value may lead to smaller v value to obtain the same QSM value (Eq. 6). Calibrated BOLD methods using gas-inhalation assumes that CBF and CMRO2 remain constant during hyperoxia (63,64). However, CBF may decrease and/or CMRO2 may increase during hyperoxia, which leads an v overestimation (62,63). The v values from the PET methods are the difference the between the total and arterial blood volume (58,59), which includes both venous and capillary blood. This may lead to larger v than the one in this study. The R2 for CGM estimated with CAT, 16.5 ± 0.5 Hz, is greater than that without CAT, 13.1 ± 0.7 Hz; and both values agree with the values calculated from other MR techniques, 14.9 ± 0.2 Hz (10), 15.1 ± 0.6 Hz (12), 17.1 ± 2 Hz (65).
In ischemic stroke patients, low OEF regions obtained by QQ with CAT are largely contained within the ischemic lesions defined by DWI (Figures 4 and 5). However, the OEF maps without CAT did not show the DWI lesion spatial pattern. The low v region with CAT generally agrees with the DWI lesion spatial pattern; this observation is consistent with the blood volume decrease in ischemic stroke lesions (66). In contrast, QQ without CAT utilized a constant OEF initial guess, and the v map contrast was similar to that of the CBF map (Figure 4). This indicates that the v result without CAT did not change much from the initial guess, which is based on the CBF through a phenomenological relationship (17–19).
In a patient imaged 12 days post stroke onset, QQ with CAT shows a distinctly different lesion OEF histogram compared to the contralateral region (Figure 5), including the strongest two peaks OEF at 0% and 17.5%, in addition to several peaks of high OEF at 35~45% that were similar to the contralateral normal OEF. The low OEF region may indicate dead tissue (OEF < 10%), while the high OEF region may represent salvageable tissue (35~45%). QQ without CAT did not show such low OEF values in the lesion. These results suggest that the use of CAT allows QQ to capture the low OEF values expected in stroke lesions.
While this work focuses on OEF and touches v, QQ also outputs R2 and χnb non-blood susceptibility maps that may provide additional biomedical values. The R2 value is reduced in ischemic regions, which is consistent with literature of elevated T2 values but is not clear in its clinical implication (67). On the other hand, χnb may be examined in QSM brain applications (68), though χnb may be difficult to interpret in white matter (69). Particularly in studies dominated by tissue iron, including multiple sclerosis (70,71), cerebral cavernous malformation (72), and Parkinson’s disease (73), it may be interesting to investigate disease effects on OEF (deoxyheme iron in blood) and non-blood (presumably dominated by tissue iron) separately.
There are limitations on using the proposed QQ with CAT. The proper number of clusters was chosen automatically by the X-means method. This is based on a well-known metric, BIC. However, the optimal number of clusters might be different when using a different metric such as the Akaike information criterion, or when using a different clustering method, such as hierarchical clustering (41,74). This might affect the resulting OEF map. However, in our study, the OEF map was not sensitive to the number of clusters (Figure 6) chosen for K-means clustering. Furthermore, the voxel-wise optimization was performed after the cluster-wise optimization, which may alleviate the consequences of the imperfect clustering. As this CAT QQ technique translates to applications in sick patients, motion compensation such as by navigators (75–77) may be employed for robustness. To improve CMRO2 estimation accuracy, CBF measurement accuracy should be increased as well. The ASL-measured CBF used in this study has low spatial resolution and may not be accurate in WM (78). The robustness of the OEF estimation is further improved by a short first echo time and a small echo spacing since the deviation from mono-exponential decay of extravascular MRI signal predominantly occurs in short TE range (Supporting Information Figures S2, S3, and S4). OEF and v estimations in large veins might be inaccurate as they were treated in the same way as normal brain tissue, which could be mitigated by using v = 1 for large veins. This may be implemented by segmenting large veins, for example by thresholding the susceptibility map (79,80), similar to the segmentation of the straight sinus. QQ with CAT optimization is still non-linear, which means that convergence may be affected by the solver implementation, parameter scaling, and stopping criterion. No ground truth or reference measurement was available. An O15 PET study on a PET-MR scanner would allow measuring accuracy in vivo.
In conclusion, our study demonstrated the feasibility of the cluster analysis of time evolution (CAT) for QSM+qBOLD (QQ) in healthy subjects and in ischemic stroke patients by effectively improving SNR. In simulations, the proposed method was more accurate than QQ without CAT. QQ with CAT provides a less noisy and more uniform OEF in healthy subjects. In ischemic stroke patients, low OEF regions are contained with the stroke lesions defined on DWI. QQ with CAT may be readily applied to investigate tissue viability in various diseases, such as Alzheimer’s disease (81,82), multiple sclerosis (83), tumor (84), and ischemic stroke (85).
Supplementary Material
Supporting Information Figure S1. The segmentations and resultant OEF maps using a different number of clusters (K = 1,5,10,15,20, as well as the X-means result, 13 indicated in red) in a healthy subject. Different colors indicate different clusters. The resulting OEF appearance is nearly constant for K ≥ 5, and were not significantly different: p=1.0000, F(5,5750075)=0.0022.
Supporting Information Figure S2. Influence of SNR on the sensitivity of the estimated Y on the initial guess with the two different TE sets 1) healthy subject TE set: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms and 2) stroke patient TE set: TE1/ΔTE/TE8 = 4.5/5/39.5 ms (Numerical Simulation 1 with the two different TE sets). Shown is the relative error between the estimated Y and the ground truth (YT). Y0 and v0 are the initial guesses of Y and v, respectively. As SNR decreases, Y becomes increasingly more sensitive to the initial guess, resulting in larger errors when the initial guess is away from the ground truth value. This is more severe in the stroke patient TE sets compared to healthy subject TE set.
Supporting Information Figure S3. OEF obtained by QQ w/ CAT with 1) healthy subject TE set: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms and 2) stroke patient TE set: TE1/ΔTE/TE8 = 4.5/5/39.5 ms at different SNRs in the simulated stroke brain (Numerical Simulation 2 with the two different TE sets). The stroke patient TE set generally showed less uniform OEF map and provided a bit worse OEF quantification compared to the healthy subject TE set, e.g. greater RMSE at all SNRs. The numbers in white indicate the OEF average and standard deviation in the whole brain, and yellow represents the root-mean-square error (RMSE).
Supporting Information Figure S4. OEF obtained by QQ w/ CAT with 1) healthy subject TE set: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms and 2) stroke patient TE set: TE1/ΔTE/TE8 = 4.5/5/39.5 ms in three healthy subjects. MRI was performed in the three healthy subjects with the two TE sets on a 3T GE scanner using mGRE, setting all the imaging parameters the same except for the TE sets: 0.85mm in-plane resolution, 1.2mm slice thickness. The healthy subject TE set generally showed more uniform OEF map, which is consistent with the Supplementary Figure 3. The numbers in white indicate the OEF average and standard deviation in the whole brain.
Supporting Information Table S1a. Scanning parameters for 11 healthy subjects (GE 3T)
Supporting Information Table S1b. Scanning parameters for 5 stroke patients (3T GE)
ACKNOWLEDGMENTS
We thank Kelly McCabe Gillen, PhD, for her assistance in manuscript editing.
REFERENCES
- 1.Derdeyn CP, Videen TO, Yundt KD, Fritsch SM, Carpenter DA, Grubb RL, Powers WJ. Variability of cerebral blood volume and oxygen extraction: stages of cerebral haemodynamic impairment revisited. Brain : a journal of neurology 2002;125(Pt 3):595–607. [DOI] [PubMed] [Google Scholar]
- 2.Gupta A, Chazen JL, Hartman M, Delgado D, Anumula N, Shao H, Mazumdar M, Segal AZ, Kamel H, Leifer D, Sanelli PC. Cerebrovascular reserve and stroke risk in patients with carotid stenosis or occlusion: a systematic review and meta-analysis. Stroke 2012;43(11):2884–2891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gupta A, Baradaran H, Schweitzer AD, Kamel H, Pandya A, Delgado D, Wright D, Hurtado-Rua S, Wang Y, Sanelli PC. Oxygen Extraction Fraction and Stroke Risk in Patients with Carotid Stenosis or Occlusion: A Systematic Review and Meta-Analysis. American Journal of Neuroradiology 2014;35(2):250–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rodgers ZB, Detre JA, Wehrli FW. MRI-based methods for quantification of the cerebral metabolic rate of oxygen. Journal of Cerebral Blood Flow & Metabolism 2016;36(7):1165–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bolar DS, Rosen BR, Sorensen A, Adalsteinsson E. QUantitative Imaging of eXtraction of oxygen and TIssue consumption (QUIXOTIC) using venular‐targeted velocity‐selective spin labeling. Magnetic resonance in medicine 2011;66(6):1550–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bulte DP, Kelly M, Germuska M, Xie J, Chappell MA, Okell TW, Bright MG, Jezzard P. Quantitative measurement of cerebral physiology using respiratory-calibrated MRI. Neuroimage 2012;60(1):582–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gauthier CJ, Hoge RD. Magnetic resonance imaging of resting OEF and CMRO2 using a generalized calibration model for hypercapnia and hyperoxia. Neuroimage 2012;60(2):1212–1225. [DOI] [PubMed] [Google Scholar]
- 8.Hoge RD. Calibrated FMRI. Neuroimage 2012;62(2):930–937. [DOI] [PubMed] [Google Scholar]
- 9.Wise RG, Harris AD, Stone AJ, Murphy K. Measurement of OEF and absolute CMRO 2: MRI-based methods using interleaved and combined hypercapnia and hyperoxia. Neuroimage 2013;83:135–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He X, Yablonskiy DA. Quantitative BOLD: mapping of human cerebral deoxygenated blood volume and oxygen extraction fraction: default state. Magn Reson Med 2007;57(1):115–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yablonskiy DA, Sukstanskii AL, He X. BOLD-based Techniques for Quantifying Brain Hemodynamic and Metabolic Properties – Theoretical Models and Experimental Approaches. NMR Biomed 2013;26(8):963–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ulrich X, Yablonskiy DA. Separation of cellular and BOLD contributions to T2* signal relaxation. Magn Reson Med 2016;75(2):606–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wehrli FW, Fan AP, Rodgers ZB, Englund EK, Langham MC. Susceptibility-based time-resolved whole-organ and regional tissue oximetry. NMR in biomedicine 2017;30(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fan AP, Benner T, Bolar DS, Rosen BR, Adalsteinsson E. Phase-based regional oxygen metabolism (PROM) using MRI. Magn Reson Med 2012;67(3):669–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jain V, Langham MC, Wehrli FW. MRI Estimation of Global Brain Oxygen Consumption Rate. Journal of Cerebral Blood Flow & Metabolism 2010;30(9):1598–1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wehrli FW, Rodgers ZB, Jain V, Langham MC, Li C, Licht DJ, Magland J. Time-resolved MRI oximetry for quantifying CMRO(2) and vascular reactivity. Academic radiology 2014;21(2):207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang J, Liu T, Gupta A, Spincemaille P, Nguyen TD, Wang Y. Quantitative mapping of cerebral metabolic rate of oxygen (CMRO2) using quantitative susceptibility mapping (QSM). Magnetic Resonance in Medicine 2015;74(4):945–952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang J, Cho J, Zhou D, Nguyen TD, Spincemaille P, Gupta A, Wang Y. Quantitative susceptibility mapping-based cerebral metabolic rate of oxygen mapping with minimum local variance. Magn Reson Med 2017. [DOI] [PubMed] [Google Scholar]
- 19.Zhang J, Zhou D, Nguyen TD, Spincemaille P, Gupta A, Wang Y. Cerebral metabolic rate of oxygen (CMRO2) mapping with hyperventilation challenge using quantitative susceptibility mapping (QSM). Magnetic resonance in medicine 2017;77(5):1762–1773. [DOI] [PubMed] [Google Scholar]
- 20.Cho J, Kee Y, Spincemaille P, Nguyen TD, Zhang J, Gupta A, Zhang S, Wang Y. Cerebral metabolic rate of oxygen (CMRO2) mapping by combining quantitative susceptibility mapping (QSM) and quantitative blood oxygenation level-dependent imaging (qBOLD). Magnetic resonance in medicine 2018;80(4):1595–1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lee H, Englund EK, Wehrli FW. Interleaved quantitative BOLD: Combining extravascular R2’ - and intravascular R2-measurements for estimation of deoxygenated blood volume and hemoglobin oxygen saturation. Neuroimage 2018;174:420–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sukstanskii AL, Yablonskiy DA. Theory of FID NMR signal dephasing induced by mesoscopic magnetic field inhomogeneities in biological systems. Journal of magnetic resonance (San Diego, Calif : 1997) 2001;151(1):107–117. [DOI] [PubMed] [Google Scholar]
- 23.Aaron Tropp J Topics in sparse approximation 2004.
- 24.Aharon M, Elad M, Bruckstein A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation 2006. 4311–4322 p.
- 25.Hongyu A, Weili L. Cerebral venous and arterial blood volumes can be estimated separately in humans using magnetic resonance imaging. Magnetic resonance in medicine 2002;48(4):583–588. [DOI] [PubMed] [Google Scholar]
- 26.Sakai F, Nakazawa K, Tazaki Y, Ishii K, Hino H, Igarashi H, Kanda T. Regional cerebral blood volume and hematocrit measured in normal human volunteers by single-photon emission computed tomography. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism 1985;5(2):207–213. [DOI] [PubMed] [Google Scholar]
- 27.Savicki JP, Lang G, Ikeda-Saito M. Magnetic susceptibility of oxy- and carbonmonoxyhemoglobins. Proceedings of the National Academy of Sciences 1984;81(17):5417–5419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hoffman R Hematology: Basic Principles and Practice: Churchill Livingstone; 2005. [Google Scholar]
- 29.Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJ. Water proton MR properties of human blood at 1.5 Tesla: magnetic susceptibility, T(1), T(2), T*(2), and non-Lorentzian signal behavior. Magn Reson Med 2001;45(4):533–542. [DOI] [PubMed] [Google Scholar]
- 30.Xu B, Liu T, Spincemaille P, Prince M, Wang Y. Flow compensated quantitative susceptibility mapping for venous oxygenation imaging. Magn Reson Med 2014;72(2):438–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu T, Khalidov I, de Rochefort L, Spincemaille P, Liu J, Tsiouris AJ, Wang Y. A novel background field removal method for MRI using projection onto dipole fields (PDF). NMR Biomed 2011;24(9):1129–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu J, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn Reson Med 2010;63(1):194–206. [DOI] [PubMed] [Google Scholar]
- 33.Liu J, Liu T, de Rochefort L, Ledoux J, Khalidov I, Chen W, Tsiouris AJ, Wisnieff C, Spincemaille P, Prince MR, Wang Y. Morphology enabled dipole inversion for quantitative susceptibility mapping using structural consistency between the magnitude image and the susceptibility map. NeuroImage 2012;59(3):2560–2568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang Y, Liu T. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn Reson Med 2015;73(1):82–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.ZA-Ohoo Liu, Spincemaille P, Yao Y, Zhang Y, Wang Y. MEDI+0: Morphology enabled dipole inversion with automatic uniform cerebrospinal fluid zero reference for quantitative susceptibility mapping. (1522–2594 (Electronic)). [DOI] [PMC free article] [PubMed]
- 36.Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal 2001;5(2):143–156. [DOI] [PubMed] [Google Scholar]
- 37.Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage 2002;17(2):825–841. [DOI] [PubMed] [Google Scholar]
- 38.Cho J, Kee Y, Spincemaille P, Nguyen T, Zhang J, Wang Y. Optimal quantitative mapping of Cerabral Metabolic Rate of Oxygen (CMRO2) by combining quantitative susceptibility mapping (QSM)-based method and quantitative BOLD (qBOLD). In Proceedings of the 25th Annual Meeting of ISMRM;Hawaii, USA, Abstract 1110. [Google Scholar]
- 39.Forgy EW. Cluster analysis of multivariate data : efficiency versus interpretability of classifications. Biometrics 1965;21:768–769. [Google Scholar]
- 40.MacQueen J Some methods for classification and analysis of multivariate observations. Fifth Berkeley Symposium on Mathematical Statistics and Probability; 1967 1967; Berkeley, Calif University of California Press; p 281–297. (Fifth Berkeley Symposium on Mathematical Statistics and Probability). [Google Scholar]
- 41.Jain AK. Data clustering: 50 years beyond K-means. Pattern Recognition Letters 2010;31(8):651–666. [Google Scholar]
- 42.Lloyd S Least squares quantization in PCM. IEEE Transactions on Information Theory 1982;28(2):129–137. [Google Scholar]
- 43.Pelleg D, Moore AW. X-means: Extending K-means with Efficient Estimation of the Number of Clusters. Proceedings of the Seventeenth International Conference on Machine Learning: Morgan Kaufmann Publishers Inc; 2000. p 727–734. [Google Scholar]
- 44.Kass RE, Raftery AE. Bayes Factors. Journal of the American Statistical Association 1995;90(430):773–795. [Google Scholar]
- 45.Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging 2001;20(1):45–57. [DOI] [PubMed] [Google Scholar]
- 46.Pei M, Nguyen TD, Thimmappa ND, Salustri C, Dong F, Cooper MA, Li J, Prince MR, Wang Y. Algorithm for fast monoexponential fitting based on Auto-Regression on Linear Operations (ARLO) of data. Magn Reson Med 2015;73(2):843–850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hansen PC. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve. SIAM Review 1992;34(4):561–580. [Google Scholar]
- 48.Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Mathematical programming 1989;45(1):503–528. [Google Scholar]
- 49.Byrd RH, Lu P, Nocedal J, Zhu C. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing 1995;16(5):1190–1208. [Google Scholar]
- 50.Baune A, Sommer FT, Erb M, Wildgruber D, Kardatzki B, Palm G, Grodd W. Dynamical Cluster Analysis of Cortical fMRI Activation. Neuroimage 1999;9(5):477–489. [DOI] [PubMed] [Google Scholar]
- 51.Heller R, Fau - Yekutieli D Stanley D, Fau - Rubin N Yekutieli D, Fau - Benjamini Y Rubin N, Benjamini Y. Cluster-based analysis of FMRI data. (1053–8119 (Print)). [DOI] [PubMed]
- 52.Liu T, Spincemaille P, de Rochefort L, Wong R, Prince M, Wang Y. Unambiguous identification of superparamagnetic iron oxide particles through quantitative susceptibility mapping of the nonlinear response to magnetic fields. Magn Reson Imaging 2010;28(9):1383–1389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. (0740–3194 (Print)). [DOI] [PubMed]
- 54.Mintun MA, Raichle ME, Martin WR, Herscovitch P. Brain oxygen utilization measured with O-15 radiotracers and positron emission tomography. Journal of nuclear medicine : official publication, Society of Nuclear Medicine 1984;25(2):177–187. [PubMed] [Google Scholar]
- 55.Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proceedings of the National Academy of Sciences 2001;98(2):676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Carpenter DA, Grubb RL Jr., Tempel LW, Powers WJ. Cerebral oxygen metabolism after aneurysmal subarachnoid hemorrhage. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism 1991;11(5):837–844. [DOI] [PubMed] [Google Scholar]
- 57.Christen T, Schmiedeskamp H, Straka M, Bammer R, Zaharchuk G. Measuring brain oxygenation in humans using a multiparametric quantitative blood oxygenation level dependent MRI approach. Magn Reson Med 2012;68(3):905–911. [DOI] [PubMed] [Google Scholar]
- 58.Ito H, Ibaraki M, Kanno I, Fukuda H, Miura S. Changes in the Arterial Fraction of Human Cerebral Blood Volume during Hypercapnia and Hypocapnia Measured by Positron Emission Tomography. Journal of Cerebral Blood Flow & Metabolism 2005;25(7):852–857. [DOI] [PubMed] [Google Scholar]
- 59.Ito H, Fau - Iida H Kanno I, Fau - Hatazawa J Iida H, Fau - Shimosegawa E Hatazawa J, Fau - Tamura H Shimosegawa E, Fau - Okudera T Tamura H, Okudera T. Arterial fraction of cerebral blood volume in humans measured by positron emission tomography. (0914–7187 (Print)). [DOI] [PubMed]
- 60.An H, Lin W. Cerebral oxygen extraction fraction and cerebral venous blood volume measurements using MRI: effects of magnetic field variation. Magn Reson Med 2002;47(5):958–966. [DOI] [PubMed] [Google Scholar]
- 61.Stone AJ, Blockley NP. A streamlined acquisition for mapping baseline brain oxygenation using quantitative BOLD. Neuroimage 2017;147:79–88. [DOI] [PubMed] [Google Scholar]
- 62.Hua J, Liu P, Kim T, Donahue M, Rane S, Chen JJ, Qin Q, Kim SG. MRI techniques to measure arterial and venous cerebral blood volume. Neuroimage 2019;187:17–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Blockley NP, Griffeth VE, Germuska MA, Bulte DP, Buxton RB. An analysis of the use of hyperoxia for measuring venous cerebral blood volume: comparison of the existing method with a new analysis approach. Neuroimage 2013;72:33–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Blockley NP, Griffeth VE, Simon AB, Buxton RB. A review of calibrated blood oxygenation level-dependent (BOLD) methods for the measurement of task-induced changes in brain oxygen metabolism. NMR in biomedicine 2013;26(8):987–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Domsch S, Mie MB, Wenz F, Schad LR. Non-invasive multiparametric qBOLD approach for robust mapping of the oxygen extraction fraction. Zeitschrift für Medizinische Physik 2014;24(3):231–242. [DOI] [PubMed] [Google Scholar]
- 66.Hatazawa J, Fau - Toyoshima H Shimosegawa E, Fau - Ardekani BA Toyoshima H, Fau - Suzuki A Ardekani Ba, Fau - Okudera T Suzuki A, Fau - Miura Y Okudera T, Miura Y. Cerebral blood volume in acute brain infarction: A combined study with dynamic susceptibility contrast MRI and 99mTc-HMPAO-SPECT. (0039–2499 (Print)). [DOI] [PubMed]
- 67.Siemonsen S, Lobel U, Sedlacik J, Forkert ND, Mouridsen K, Ostergaard L, Thomalla G, Fiehler J. Elevated T2-values in MRI of stroke patients shortly after symptom onset do not predict irreversible tissue infarction. Brain 2012;135(Pt 6):1981–1989. [DOI] [PubMed] [Google Scholar]
- 68.Wang Y, Spincemaille P, Liu Z, Dimov A, Deh K, Li J, Zhang Y, Yao Y, Gillen KM, Wilman AH, Gupta A, Tsiouris AJ, Kovanlikaya I, Chiang GC, Weinsaft JW, Tanenbaum L, Chen W, Zhu W, Chang S, Lou M, Kopell BH, Kaplitt MG, Devos D, Hirai T, Huang X, Korogi Y, Shtilbans A, Jahng GH, Pelletier D, Gauthier SA, Pitt D, Bush AI, Brittenham GM, Prince MR. Clinical quantitative susceptibility mapping (QSM): Biometal imaging and its emerging roles in patient care. J Magn Reson Imaging 2017;46(4):951–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wisnieff C, Liu T, Spincemaille P, Wang S, Zhou D, Wang Y. Magnetic susceptibility anisotropy: cylindrical symmetry from macroscopically ordered anisotropic molecules and accuracy of MRI measurements using few orientations. Neuroimage 2013;70:363–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Chen W, Gauthier SA, Gupta A, Comunale J, Liu T, Wang S, Pei M, Pitt D, Wang Y. Quantitative Susceptibility Mapping of Multiple Sclerosis Lesions at Various Ages. Radiology 2014;271(1):183–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wisnieff C, Ramanan S, Olesik J, Gauthier S, Wang Y, Pitt D. Quantitative susceptibility mapping (QSM) of white matter multiple sclerosis lesions: Interpreting positive susceptibility and the presence of iron. Magn Reson Med 2015;74(2):564–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tan H, Liu T, Wu Y, Thacker J, Shenkar R, Mikati AG, Shi C, Dykstra C, Wang Y, Prasad PV, Edelman RR, Awad IA. Evaluation of iron content in human cerebral cavernous malformation using quantitative susceptibility mapping. Invest Radiol 2014;49(7):498–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Murakami Y, Kakeda S, Watanabe K, Ueda I, Ogasawara A, Moriya J, Ide S, Futatsuya K, Sato T, Okada K, Uozumi T, Tsuji S, Liu T, Wang Y, Korogi Y. Usefulness of quantitative susceptibility mapping for the diagnosis of Parkinson disease. AJNR Am J Neuroradiol 2015;36(6):1102–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Wilks DS. Chapter 15 - Cluster Analysis In: Wilks DS, editor. International Geophysics. Volume 100: Academic Press; 2011. p 603–616. [Google Scholar]
- 75.Wang Y, Rossman PJ, Grimm RC, Wilman AH, Riederer SJ, Ehman RL. 3D MR angiography of pulmonary arteries using real-time navigator gating and magnetization preparation. Magn Reson Med 1996;36(4):579–587. [DOI] [PubMed] [Google Scholar]
- 76.Nguyen TD, Nuval A, Mulukutla S, Wang Y. Direct monitoring of coronary artery motion with cardiac fat navigator echoes. Magn Reson Med 2003;50(2):235–241. [DOI] [PubMed] [Google Scholar]
- 77.Skare S, Hartwig A, Martensson M, Avventi E, Engstrom M. Properties of a 2D fat navigator for prospective image domain correction of nodding motion in brain MRI. Magn Reson Med 2015;73(3):1110–1119. [DOI] [PubMed] [Google Scholar]
- 78.Gardener AG, Jezzard P. Investigating white matter perfusion using optimal sampling strategy arterial spin labeling at 7 Tesla. Magnetic resonance in medicine 2015;73(6):2243–2248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Fan AP, Bilgic B, Gagnon L, Witzel T, Bhat H, Rosen BR, Adalsteinsson E. Quantitative oxygenation venography from MRI phase. Magnetic resonance in medicine 2014;72(1):149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Haacke EM, Tang J, Neelavalli J, Cheng YCN. Susceptibility mapping as a means to visualize veins and quantify oxygen saturation. Journal of Magnetic Resonance Imaging 2010;32(3):663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Sun X, He G, Qing H, Zhou W, Dobie F, Cai F, Staufenbiel M, Huang LE, Song W. Hypoxia facilitates Alzheimer’s disease pathogenesis by up-regulating BACE1 gene expression. Proceedings of the National Academy of Sciences of the United States of America 2006;103(49):18727–18732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Acosta-Cabronero J, Williams GB, Cardenas-Blanco A, Arnold RJ, Lupson V, Nestor PJ. In vivo quantitative susceptibility mapping (QSM) in Alzheimer’s disease. PloS one 2013;8(11):e81093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Trapp BD, Stys PK. Virtual hypoxia and chronic necrosis of demyelinated axons in multiple sclerosis. The Lancet Neurology 2009;8(3):280–291. [DOI] [PubMed] [Google Scholar]
- 84.Stadlbauer A, Zimmermann M, Kitzwogerer M, Oberndorfer S, Rossler K, Dorfler A, Buchfelder M, Heinz G. MR Imaging-derived Oxygen Metabolism and Neovascularization Characterization for Grading and IDH Gene Mutation Detection of Gliomas. Radiology 2017;283(3):799–809. [DOI] [PubMed] [Google Scholar]
- 85.Kudo K, Liu T, Murakami T, Goodwin J, Uwano I, Yamashita F, Higuchi S, Wang Y, Ogasawara K, Ogawa A, Sasaki M. Oxygen extraction fraction measurement using quantitative susceptibility mapping: Comparison with positron emission tomography. Journal of cerebral blood flow and metabolism : official journal of the International Society of Cerebral Blood Flow and Metabolism 2016;36(8):1424–1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Figure S1. The segmentations and resultant OEF maps using a different number of clusters (K = 1,5,10,15,20, as well as the X-means result, 13 indicated in red) in a healthy subject. Different colors indicate different clusters. The resulting OEF appearance is nearly constant for K ≥ 5, and were not significantly different: p=1.0000, F(5,5750075)=0.0022.
Supporting Information Figure S2. Influence of SNR on the sensitivity of the estimated Y on the initial guess with the two different TE sets 1) healthy subject TE set: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms and 2) stroke patient TE set: TE1/ΔTE/TE8 = 4.5/5/39.5 ms (Numerical Simulation 1 with the two different TE sets). Shown is the relative error between the estimated Y and the ground truth (YT). Y0 and v0 are the initial guesses of Y and v, respectively. As SNR decreases, Y becomes increasingly more sensitive to the initial guess, resulting in larger errors when the initial guess is away from the ground truth value. This is more severe in the stroke patient TE sets compared to healthy subject TE set.
Supporting Information Figure S3. OEF obtained by QQ w/ CAT with 1) healthy subject TE set: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms and 2) stroke patient TE set: TE1/ΔTE/TE8 = 4.5/5/39.5 ms at different SNRs in the simulated stroke brain (Numerical Simulation 2 with the two different TE sets). The stroke patient TE set generally showed less uniform OEF map and provided a bit worse OEF quantification compared to the healthy subject TE set, e.g. greater RMSE at all SNRs. The numbers in white indicate the OEF average and standard deviation in the whole brain, and yellow represents the root-mean-square error (RMSE).
Supporting Information Figure S4. OEF obtained by QQ w/ CAT with 1) healthy subject TE set: TE1/ΔTE/TE7 = 2.3/3.9/25.8 ms and 2) stroke patient TE set: TE1/ΔTE/TE8 = 4.5/5/39.5 ms in three healthy subjects. MRI was performed in the three healthy subjects with the two TE sets on a 3T GE scanner using mGRE, setting all the imaging parameters the same except for the TE sets: 0.85mm in-plane resolution, 1.2mm slice thickness. The healthy subject TE set generally showed more uniform OEF map, which is consistent with the Supplementary Figure 3. The numbers in white indicate the OEF average and standard deviation in the whole brain.
Supporting Information Table S1a. Scanning parameters for 11 healthy subjects (GE 3T)
Supporting Information Table S1b. Scanning parameters for 5 stroke patients (3T GE)


