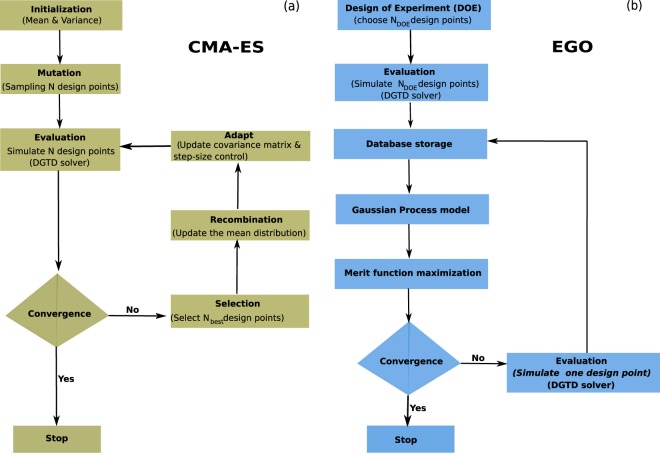
Figure 1.

For the CMA-ES (a), the optimization starts with an initial design and a given mean and variance. The second step consists in generating a population of N designs that will be evaluated using the fullwave DGTD solver. If the convergence is not satisfied, the algorithm chooses the N_best designs according to the objective function, and use them to update the mean of the distribution, size and the covariance matrix. N new designs are thereafter calculated and repeated steps until the convergence criterion is reached. For the EGO (b) instead, the algorithm starts with an initial design of experiments composed of N_DOE designs, that will be simulated to estimate the corresponding objective function. The results are used to construct a surrogate model, of interest to search for the next design. The latter is simulated using the fullwave DGTD solver, and the corresponding objective value enrich the database, repeating these steps until the convergence is obtained. The major difference between the CMA-ES and EGO methods essentially relies on the utilization of a surrogate model for EGO that drastically reduces the number of evaluations N_DOE by an order of magnitude.