Learning accurate representations of microbe-metabolite interactions

Abstract

Integrating multi-omics datasets is critical for microbiome research, but multiple statistical challenges can confound traditional correlation techniques. We solve this problem by using neural networks to estimate the conditional probability that each molecule is present given the presence of each specific microbe. We show with known environmental (desert biological soil crust wetting) and clinical (cystic fibrosis lung) examples, our ability to recover microbe-metabolite relationships, and demonstrate how the method can discover relationships between microbially-produced metabolites and inflammatory bowel disease.

2. Introduction

Knowledge gained by integrating complementary “-omics” data with a multi-omics approach will lead to improved diagnostics, automated drug discovery, and optimized culturing conditions for uncharacterized microbes [1]. Previous work have been able to predict metabolite abundance profiles from microbe abundance profiles [2, 3]. However, because conventional correlation techniques have unacceptably high false discovery rates, finding meaningful relationships between genes within complex microbiomes and their products in the metabolome is challenging.

Although there has been a widespread effort to develop multi-omics approaches, several conceptual challenges limit techniques that integrate disparate “omics” data in general, including linking the microbial sequencing and untargeted mass spectrometry. Therefore, new approaches are needed that can handle disparate data types [4]. Relative abundances of thousands of microbes and metabolites can be measured using sequencing and mass spectrometry, resulting in the generation of very high dimensional microbiome and metabolomics datasets. Quantifying microbe-metabolite interactions from these abundances requires estimating a distribution across all possible microbe-metabolite interactions.

Techniques such as Canonical Correspondence Analysis (CCA) and Partial Least Squares (PLS) approximate this joint distribution using a low dimensional representations [5, 6, 7]. Network models have been shown to improve classification accuracy using multiple datasets [8]. Factor models have been proposed to incorporate multiple datasets for biomarker analysis [9]. Despite of the wide application of these methods, they are notoriously difficult to interpret [10, 11, 12] and it remains unclear whether these models can obtain individual microbe-metabolite interactions.

Pearson and Spearman correlations assume independence between interactions, simplifying the estimation procedure by reducing it to a combination of independent two dimensional problems. However, many studies have shown that these methods are not statistically valid for compositional data, a fact first recognized by Pearson in 1895 and followed up in numerous studies [13, 14, 15, 16, 17]. This problem is further complicated because both microbiome [17] and mass spectrometry [18, 19, 20, 21] datasets are also compositional, meaning that the absolute abundances are not measured, which can confound statistical inference. For example, in untargeted mass spectrometry experiments, the set of molecules detected and their relative abundance vary depending on the extraction protocol and analytic methods used, which leads to only a partial snapshot of the metabolome. Moreover, measuring the total mass of molecules extracted is often not performed in large scale metabolomics efforts, due to the highly laborious nature of that step.

To understand how issues associated with compositional data impact inference on microbe-metabolite interactions, consider the example in Figure S1. There are two microbes and two metabolites in Figure S1a. All are increasing exponentially at different rates and are highly correlated with each other. If proportions are estimated from the absolute abundances via sampling, the information about the total microbe population size and the total metabolite abundance is lost, and the correlations between the microbes and the metabolites disappear. False positives can also appear as shown in Figure S1b, microbe and metabolite interactions that have no apparent correlation structure may appear to be correlated when investigating the proportions. These issues alone can give rise to overwhelming false positives and false negatives, making Pearson and Spearman in some scenarios comparable to random coin flips. Experimental validation currently takes large laboratories multiple years to perform [22], often requiring time-consuming manual examinations of erroneous correlations.

There are other compositional techniques such as SparCC[13] and proportionality[23] that are scale-invariant when analyzing a single dataset, but lose scale-invariance when analyzing multiomics datasets. This was shown in the context of identifying microbe-fungal interactions [24], which provided motivation to extend SPIEC-EASI [14] to handle multiomics datasets. We show that this approach does not work for microbe-metabolite interactions because of differences of measurement units between sequencing and mass spectrometry measurements (Supplementary materials). An alternative approach is to consider co-occurrence probabilities instead of correlations. Here, co-occurrence probabilities refer to the conditional probability of observing a metabolite given that a microbe was observed, thereby allowing us to identify the most likely microbe-metabolite interactions. To do this, we propose “mmvec”, (microbe-metabolite vectors), to learn these co-occurrence probabilities between microbes and metabolites (Figure 1). Due to its scale-robustness properties, the microbial-metabolite relationships learned by mmvec are consistent between the absolute and relative abundances. The microbe-metabolite interactions can be ranked [25] and visualized through standard dimensionality reduction interfaces, enabling interpretable findings. The computations behind mmvec can take advantage of modern GPU architectures using Tensorflow [26], enabling scalable inference on large multiomics datasets. Furthermore, we provide evidence in two benchmarks and four case studies that mmvec outperforms existing statistical methods.

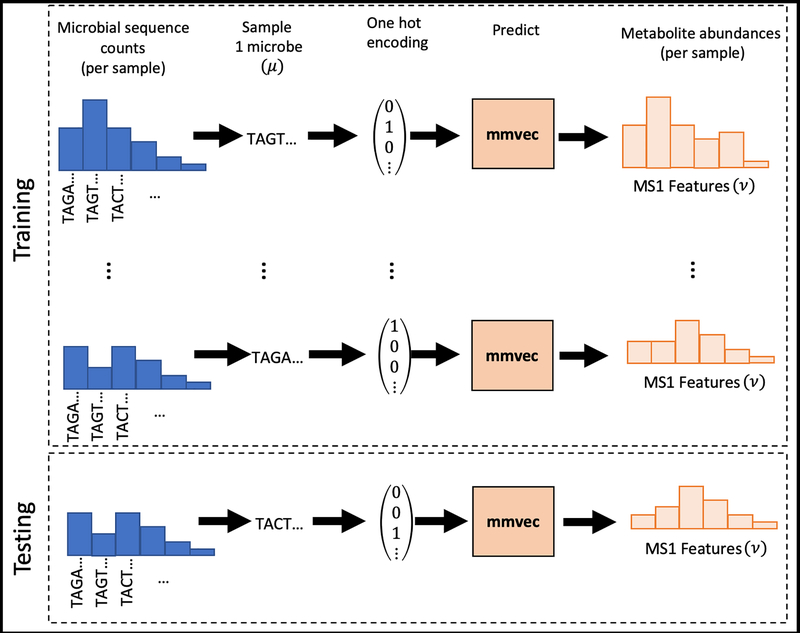
Figure 1:

Input data types and mmvec neural network architecture. (a) The neural network architecture where the input layer represents one-hot encodings of N microbes and the output layer represents the proportions of M metabolites. U corresponds to microbial vectors and V corresponds to metabolite vectors. (b) The pipeline for training mmvec. The objective behind mmvec is to predict metabolite abundances (y) given a single input microbe sequence (x), also known as a one-hot encoding. This training procedure will estimate conditional probabilities of observing a metabolite given the input microbe sequence. Cross-validation can be performed on hold-out samples to access overfitting.

3. Results and Discussion

We performed benchmarks comparing mmvec to Pearson, Spearman, SPIEC-EASI, SparCC and Proportionality [23] using a cystic fibrosis biofilm simulation. We then show that mmvec can resolve contradictory cyanobacteria-metabolite relationships in a desert soil biocrust wetting study. We also demonstrate recovery of known associations of P. aeruginosa-produced metabolites observed in cystic fibrosis [27]. Finally, we explore the relationships of microbiota and metabolic changes in mice fed a high fat diet [28] and inflammatory bowel disease [29], showing how this approach can be used to determine microbial origin of novel molecules even in extremely complex real-life biological systems with limited knowledge of existing associations.

3.1. Simulation benchmarks

To compare mmvec performance to Pearson, Spearman, Proportionality, SparCC and SPIEC-EASI correlations, we used data from existing studies in which the relationships between microbes and metabolites were the central focus of investigation. One such study simulated spatial-temporal dynamics in a microbial biofilm [27]. The original study tested the hypothesis that the cystic fibrosis (CF) microbiome community within human lungs can be manipulated by altering its chemical environment. Changes in pH and oxygen saturation suppress the principal pathogen, P. aeruginosa, without using antibiotics, by promoting the growth of a community of fermenters that out-compete the pathogen. The simplicity of this system allowed the high-level ecological patterns to be modelled. In the original simulations, the interactions between two microbes (fermenters denoted by Θ_f and P. aeruginosa denoted by Θ_p) and multiple molecules were modeled using Monad kinetics and diffusion processes[27] (Figure 2a).

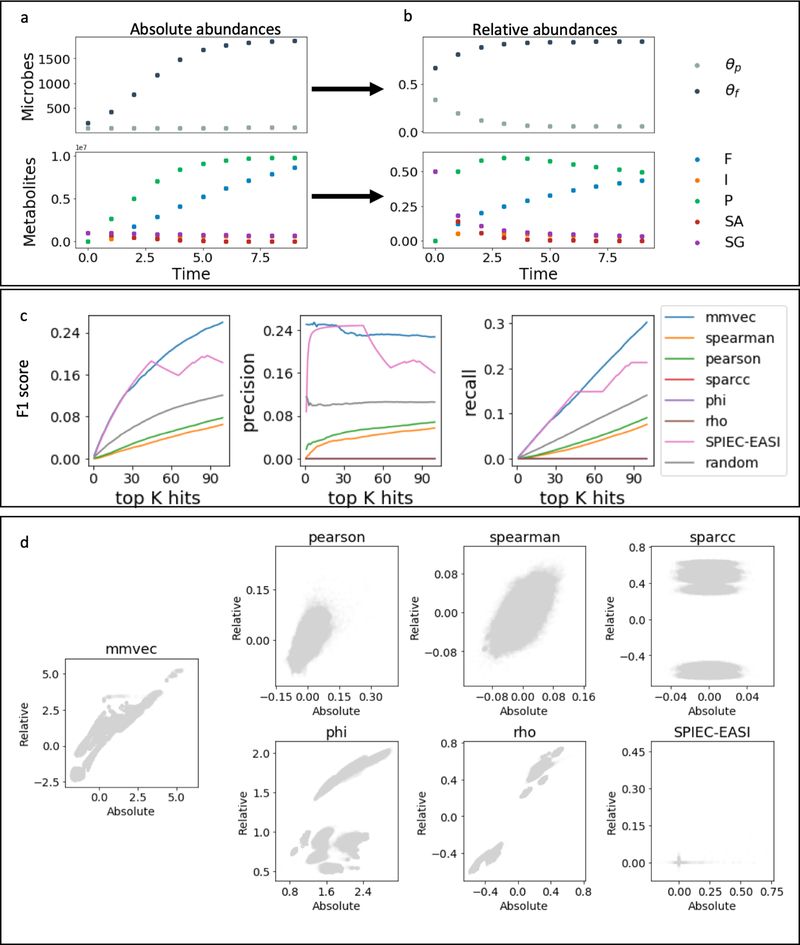
Figure 2:

Simulation benchmarks. (a) Absolute abundances of microbes and metabolites simulated from differential equations derived in [27] for a specific spatial point. (b) Proportions of the abundances shown in (a). (c) F1 score, precision and recall curves comparing mmvec to Pearson, Spearman, SparCC, SPIEC-EASI, and proportionality metrics phi and rho across the top 100 metabolites for each microbe. (d) comparisons of coefficients learned from absolute abundances and relative abundances all of the benchmarked methods.

We simulated the measurement process for microbial DNA sequencing and untargeted mass spectrometry for metabolites as discussed in the Online Methods, providing ground truth information on their interactions. The model simulates interactions between P. aeruginosa and the fermenters, and their interactions with the environment. It also simulates known interactions between microbes and molecules, such as sugar consumption by fermenters and ammonia production by the pathogen. For example, the fermenters are positively associated with sugars and ammonium concentration, and negatively associated with inhibitor concentration; P. aeruginosa is positively associated with amino acids and pH.

Therefore, we can test whether the top K metabolites associated with each microbe by each tool includes the correct microbe-metabolite interactions. Figure 2c shows specificity and sensitivity for each tools as a function of K. In these simulations, random chance outperformed all of the tools except for mmvec and SPIEC-EASI, with mmvec performing the best. As shown in Figure 2d and Figure S2, mmvec is the only method robust to scale deviations amongst the methods tested. This is critical for maintaining consistency between absolute and relative abundances, which can otherwise lead to inflated false positives and false negatives [16].

3.2. Soil biocrust wetting event case study

Many studies produce inconsistent results that can be resolved with improved data analysis, especially in environmental and clinical settings. To test whether mmvec can resolve unexplained discrepancies in microbe-metabolite interactions across studies, we applied it to a study of biocrust wetting [30]. In this study, laboratory-based exometabolite patterns observed with bacterial isolates were reproduced in the environment. Specifically, in this work authors identified metabolites that were consumed and released by multiple biocrust isolates including Microcoleus vaginatus and two Bacillus strains [31], and compared these patterns with closely-related environmental taxa and metabolites observed in situ [30].

While almost 70% of the examined microbe-metabolite relationships following the wetting event were validated [30], some contradicted the microbe-metabolite relationships observed in cultures [31]. These contradictions stemmed from Spearman correlations between M. vaginatus abundances and the observed metabolite abundances, but were resolved by mmvec (Figure 3a).

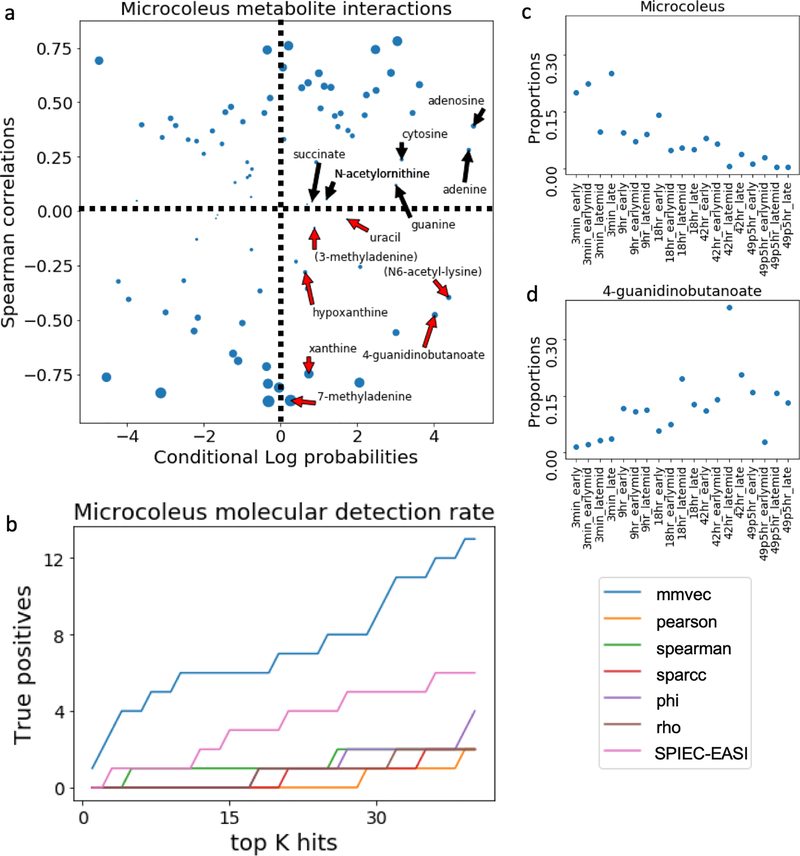
Figure 3:

M. vaginatus released metabolites after the biocrust wetting event. (a) Comparison of M. vaginatus metabolite interactions estimated from Spearman and mmvec from (n=19 samples). All of the experimentally validated M. vaginatus released metabolites are labeled. All metabolites with contradicting findings between the wetting experiment and the in vitro experimental results are highlighted in red. Points are resized according to the −10 log(p-value) obtained from Spearman correlation. Dashlines mark the cutoff for a Spearman correlation of zero, and the conditional log probabilities of zero. Here a zero log conditional probability represents the conditional probability of the average metabolite because all probabilities here are mean centered. (b) Benchmarks comparing the detection rate of the experimentally validated molecules across different statistical methodologies. (c) M. vaginatus proportions and (d) 4-guanidinobutanoate proportions following a wetting event.

All metabolites released from the M. vaginatus isolate have higher conditional probabilities than the average metabolite following biocrust wetting, and are among the top 80 co-occurring metabolites with M. vaginatus (of 485 molecules total). This result supports the original finding that M. vaginatus actually releases these molecules after the wetting event. In contrast, Spearman labels 7 of 13 of these molecules with a negative correlation, indicating that these molecules were consumed by M. vaginatus rather than released, as originally stated in [30]. When the annotation detection rates amongst different statistical methodologies, mmvec has a substantially higher true positive rate as shown in Figure 3b.

The conflicting results between mmvec and Spearman could be explained by the growing microbial biomass and shift in available resources after wetting (Figure 3 c, d). Total biomass is expected to increase, because M. vaginatus releases metabolites that enable the growth of many other microbes. Because DNA sequencing can only measure proportions, the growth in other microbes could cause the proportions of M. vaginatus to decrease, leading to a misleading anti-correlation with 4-guanidinobutanoate (Figure 3d). However, it is not possible to infer whether M. vaginatus is decreasing in abundance [25] or 4-guanidinobutanoate is increasing in abundance.

The change in the total biomass and the total available resources could explain the contradiction between the Spearman correlations and the isolate results. M. vaginatus likely grows at a slower rate relative to other microbes that benefit from the metabolite release. Because mmvec does not rely on knowledge of the total biomass or normalize to relative abundance, these contradictions are avoided.

3.3. Cystic Fibrosis case study

To further validate if mmvec can detect known microbe-metabolite interactions in a biological setting, we re-analyzed a study on lung mucus microbiome of patients with cystic fibrosis [27, 32]. Cystic fibrosis has been shown to be dominated by two major groups of microbes, anaerobes and pathogens that occupy unique niches, and their interactions are defined by the environment. Anaerobes dominate in low oxygen and low pH environments, while pathogens, in particular P. aeruginosa, dominate in the opposite conditions [27]. Mmvec clearly separates anaerobes and pathogens (Figure 4a), with known anaerobic microbes (Veillonella, Fusobacterium, Prevotella and Streptococcus) on the left, and notable pathogens, such as P. aeruginosa, on the right.

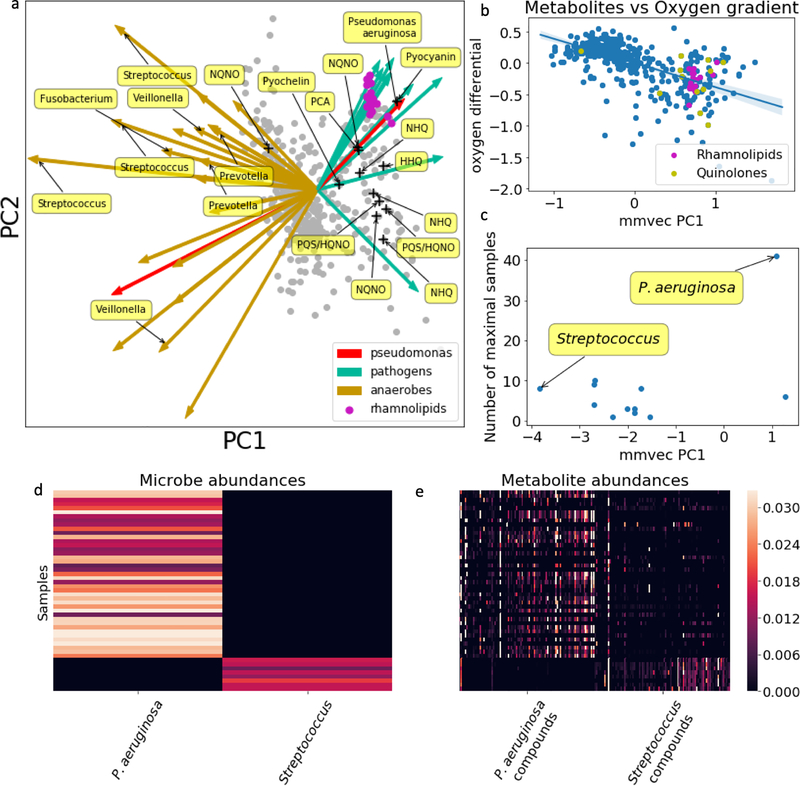
Figure 4:

Investigation of P.aeruginosa-associated molecules. (a) Biplot drawn from the mmvec conditional probabilities estimated for the cystic fibrosis dataset [27]. Arrows represent microbes and dots represent metabolites. The x and y axes represent principal components from the SVD of the microbe-metabolite conditional probabilities estimated from mmvec (n=138 samples). Distances between points quantify co-occurrence strength between metabolites, with small distances indicating metabolites that have a high probability of co-occurring with high probability. Distances between arrow tips quantify co-occurrence strength between microbes. The directionality of the arrows can be used to pinpoint which microbes can explain the metabolite co-occurrence patterns. Arrows highlighted in green correspond to putative cystic fibrosis pathogens and yellow arrows highlight known anaerobes. Only known molecules produced by P. aeruginosa are labeled. (b) Scatter plot of molecules with respect to the oxygen gradient differential and the first principal component learned from mmvec (n=442 molecules) with linear regression model and 95% confidence interval for regression estimate. (c) The first principal component vs the number of samples where the taxa was the most abundant taxa in that sample. (d) Heatmap of P. aeruginosa and Streptococcus abundances in samples where they are the most abundant species. (e) Heatmap of the top 100 molecules that co-occur with P. aeruginosa and Streptococcus.

P. aeruginosa is known to produce small-molecule virulence factors [33]. In the original study, based on annotations from GNPS[34], the bacterium was found to produce six molecules: 4-hydroxy-2-heptylquinoline (HHQ), Pyocyanin (PYO), Phenazine-1-carboxylic acid (PCA), 2-nonyl-4-hydroxy-quinoline (NHQ), 2-heptyl-3,4-dihydroxyquinoline (PQS, Pseudomonas quinolone signal) and Pyochelin [27]. As shown in Figure 4a, mmvec identifies these molecules with a high co-occurrence probability with P. aeruginosa. Mmvec also identifies a cluster of rhamnolipids likely produced by P. aeruginosa. Rhamnolipids are well characterized and are an important virulence factors for P. aeruginosa, contributing to biofilm development, motility on surfaces and antagonistic interactions with host inflammatory cells [35, 36]. These rhamnolipids were not identified in the original study [27]. The annotations for these compounds have been estiblished using GNPS [34].

There is a negative correlation between the first principal component learned from mmvec and the metabolites log-fold change across the oxygen gradient (Figure 4b) (Pearson r=−0.59, p-value 1.8×10⁻⁴⁴, n=442 molecules), which is consistent with the findings in the original work. No such correlation between the oxygen gradient and the first microbial principal component was found by Pearson (r=0.11, p=0.16, n=138 microbes). There exist two notable microbes on opposing ends of the first microbial principal component: P. aeruginosa, a known pathogen, and Streptococcus, a known anaerobe. The top 100 metabolites that are specific to P. aeruginosa and Streptococcus are shown to have drastically different profiles in samples where P. aeruginosa and Streptococcus were the most abundant species (Figure 4d,e) (logratio t-test=6.51, p=4.4×10⁻⁸, n=49 samples). This provides evidence that in the context of this study, the metabolomic profiles can be largely influenced by the most abundant microbes, a notion that has important implications for understanding CF etiology. To further support this, the learned metabolite conditional probabilities for P. aeruginosa can be used to predict the metabolite proportions in the 41 samples where P. aeruginosa is the most abundant taxa. The predicted P. aeruginosa metabolite profiles alone can explain 10% of the metabolite variation in these samples (r=0.319, p=1.18×10⁻¹¹, n=442 molecules).

Of 14 quinolone molecules known to be produced by P. aeruginosa, Pearson correlation detected 9 with p<0.05 without FDR correction, and only 5 with FDR correction. For example, Pyocyanin, does not appear related to P. aeruginosa by the raw proportions (r=0.158, FDR-corrected pvalue=0.089, rank=96, n=172 samples), but is ranked 34th most associated with P. aeruginosa by mmvec (Figure S3c), consistent with culturing experiments that demonstrate that P. aeruginosa produces this molecule [37]. 18 rhamnolipids are among the top 25 metabolites most associated with P. aeruginosa by mmvec, and have higher ranks with mmvec than with Pearson correlation (Figure S3b).

3.4. Effects of high fat diet in murine model case study

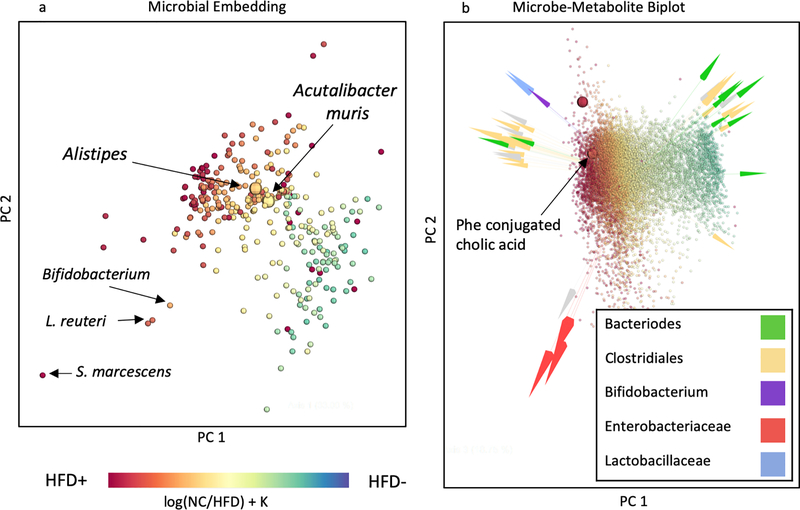
We then tested whether mmvec could determine the microbial origin of specific molecules in a complex biological system. We recently discovered a new kind of bile acid, where cholate is conjugated to amino acids other than glycine and taurine [38]. These molecules increased in abundance with high-fat diet in humans. We determined that these molecules are microbially-made since they were present in specific pathogen free, but not in germ free mice. We therefore set out to identify candidate producers. We were able to confirm that one of these bile acids, cholate phenylalanine amidate, was associated with high-fat diet in well-controlled study that investigated the development of non-alcoholic fatty liver disease (NAFLD), cirrhosis, and hepatocarcinoma (HCC) in a mouse model [28]. When re-analyzing these datasets for differential abundances via multinomial regression, the strong association of the novel bile acid with HFD became immediately apparent. The use of mmvec showed distinct associated groups of microbes and HFD (Figure 5a) and a clear stratification of the mass spectrometry data according to diet (Figure 5b). Several Clostridium spp. correlated with the cholate phenylalanine conjugate. Indeed, we showed that Clostridium spp. were found to produce this bile acid [38]. This result demonstrates mmvec’s ability to streamline the discovery of microbes that produce specific molecules of interest in vivo.

Figure 5:

Microbe/metabolite co-occurrences across study of HCC progression in the context of innate immunity in a mouse model [28]. (a) Visualization of microbial co-occurrence patterns, where distances between points approximates the Aitchison distance between microbes, which quantities microbial occurrences. Small distances are indicative of microbes with high probability of co-occurring together. Microbes are colored according to their association with HFD, which was estimated using differential abundance analysis via multinomial regression. (b) Emperor [59] biplot of microbe-metabolite interactions, with metabolites colored according to their association with HFD. HFD association was estimated through differential abundance analysis via multinomial regression. Distances between points approximate Aitchison distances between metabolites and distances between arrow tips approximate Aitchison distances between microbes. Several Clostridium spp. appear to co-occur with the new bile acid molecule cholate phenylalanine amidate, also referred to as Phe conjugated cholic acid.

3.5. Microbe-metabolite interactions in Inflammatory Bowel Disease

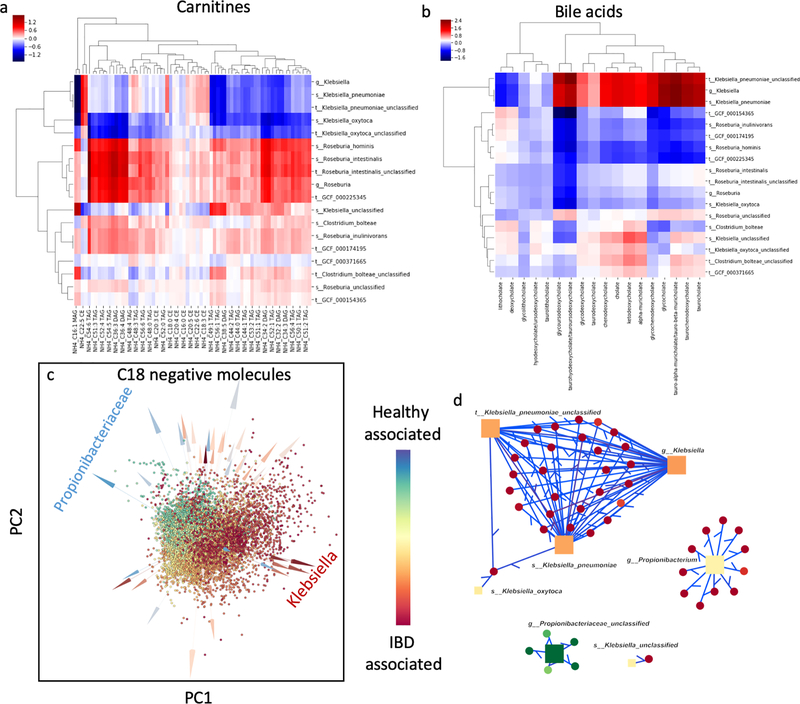
Finally, microbe-metabolite interactions were investigated for samples of IBD patients generated under the integrative Human Microbiome Project [29]. The role of the microbiome in IBD is acknowledged, but still poorly understood. The original study uncovered shifts in metabolomic and microbial profiles associated with the IBD. In particular, levels of carnitines and bile acids were shown to be affected [29]. Using mmvec we confirmed the core findings in the previous study, such as the co-occurrence between R. hominis and multiple carnitines, including previously noted C20, which have anti-inflammatory properties (Figure 6a) [29]. We also found high correlation of Klebsiella spp. with IBD status and that it co-occurs with high probability with several bile acids (Figure 6b). Although Klebsiella itself does not produce these compounds, some pathogens (including Klebsiella) are known to be resistant to bile acids [39]. Excessive production of some bile acids and bile acid malabsorption can lead to overabundance of bile acids, which is a hallmark of IBD [40], although the exact mechanisms remain unknown. The ability of Klebsiella to thrive in concentrated bile acid environments is consistent with the high co-occurrence probabilities shown in Figure 6b. We also noted that three Klebsiella species are the top drivers of the IBD-associated molecules (Figure 6c). It is important to delineate different reasons for co-occurrence. Unlike Klebsiella, Clostridium species are known for bile acid manipulation, including production of bile that can germinate Clostridium difficile spores or that have anti-microbial properties [41, 42].

Figure 6:

Microbe-metabolite interactions of the human microbiome in association with IBD samples [29]. (a) Heatmap visualization of the inferred conditional probabilities for various bile acids given the presence of Klebsiella, Roseburia and Clostridium bolteae. (b) Heatmap visualization of the inferred conditional probabilities for the carnitines given the presence of Klebsiella, Roseburia, and Clostridium bolteae. (c) Multiomics biplot of the microbe-metabolite interactions learned from metagenomics profiles and C18 negative ion mode LC-MS. Microbes (arrows) and metabolites (spheres) are colored according to their differentials estimated from multinomial regression. Klebsiella spp. appears to be strongly associated with IBD, while Propionibacterium spp. has strong negative association. (d) Network of the top 300 edges where only the edges that contain Klebsiella and Propionibacteriaceae are visualized.

Therefore, it is possible that in case of Clostridia, the existing co-occurrences (Figure 6b) are due to actual biosynthesis of the metabolites by the microbial species indicated rather than ability to withstand them.

In addition to recapitulating reported findings, mmvec also yielded previously undetected relationships. The major microbe that was found to be associated with healthy patients is Propionibacteriaceae, which was not detected in Price et al 2019 (Figure 6cd). This relationship is corroborated by other published studies. In one study, it has been shown that some members of the Propionibacterium genus produce 1.4-Dihydroxy-2-naphthoic acid (DHNA), a growth stimulator for bacteria such as Bifidobacterium that are thought to reduce the symptoms of IBD [43]. Also, in a survey of in vivo vs. in vitro bacterial activity, Probionibacterium freudenreichii was shown to play an immunomodulatory role in the context of an ulcerative colitis mice model [44]. In another study it was shown that Propionibacterium freudenreichii is a viable core component in an anti-inflammatory probiotic fermented dairy product [45]. The members of this family have been considered beneficial for intestinal immunoregulation; Propionibacteriaceae have been observed to be enriched in human breast milk and have been shown to restore Th17 differentiation [46]. Thus, it appears that the existing knowledge supports the statistically-inferred interaction uncovered by mmvec, but not identified in the published analysis of the dataset.

4. Conclusion

In both simulation benchmarks and annotated dataset, mmvec shows promise for inferring microbe-metabolite interactions from multiomics datasets. Our benchmarks suggest that mmvec outperforms all existing tools that aim to infer interactions between paired microbe-metabolite abundance datasets, both in simulations and in experimental data. In the biocrust wetting experiment, mmvec resolved conflicting findings between the in vitro validated M. vaginatus released metabolites and the sequencing/mass spectrometry analysis of environmental samples. In the cystic fibrosis study, mmvec can reliably identify all of the experimentally determined P. aeroginosa-produced molecules of interest. We show in the example of bile acid production that mmvec enables exploratory analysis in complex biological systems and streamlined discovery of the microbial origin of specific metabolites. Finally, mmvec was able to identify the strongest microbial contributions to the metabolite abundances in the IBD study, where one of those microbes was missed in the original study.

In light of these findings, the current methodology still has limitations. It remains unclear how to access statistical significance of an interaction using co-occurrence probabilities. Similarly, confidence intervals for the strength of each microbe-metabolite interaction can not yet be calculated. Furthermore, more theoretical work will be required to handle continuous-valued inputs.

The concepts outlined here should generalize beyond microbe-metabolite interactions to handle other paired multi-omic data types, provided that the input dataset is made up of counts (as in metagenomics, transcriptomics, etc.). With the exponential growth of multiomics datasets, there is much potential to use these methods to reveal microbial metabolism, including for microbes that are not cultivable in the laboratory. Approaches utilizing co-occurrence probabilities have the potential to enable more targeted experimental assays, accelerating the discovery of microbe-metabolite interactions, paving the way towards new ecosystems engineering approaches in clinical, environmental and industrial applications.

10. Methods

10.1. Mmvec neural network architecture

The development of our proposed neural network was inspired by applications in natural language processing. The underlying model can also be referred to as a bi-loglinear multinomial regression. Our mmvec model posits an assumed generative process for the data, which leads to an inference algorithm to recover the model’s parameters from multi-omics data. The model’s assumed generative model for metabolite ν, microbe μ and sample k given as follows.

First generate microbe vector u_μ for microbe μ∈{1,...N} and metabolite vectors v_ν for metabolite ν∈{1,...M},

$${\mathbf{u}}_{\mathrm{\mu }}\sim \mathcal{N}(\mathbf{0},{\mathrm{\sigma }}_{u}I){\mathbf{v}}_{\mathbf{\nu }}\sim \mathcal{N}(\mathbf{0},{\mathrm{\sigma }}_{v}I),$$

These vectors are length p, corresponding to the number of latent vectors dimensions. Each of these vectors are drawn from a normal prior centered around zero and a diagonal covariance matrix with variances σ_u and σ_v, namely to serve regularization purposes and avoid overfitting. For a given microbial sample x_k, the models generative process draws a single microbe from a single draw from the categorical distribution

$$\mathrm{\mu }\sim Categorical({\mathbf{x}}_{\mathbf{k}}).$$

That microbe μ can be used to index U in order to generate conditional probabilities q_μ

$$p(\mathrm{\nu }|\mathrm{\mu })=\frac{\exp \left({\mathbf{v}}_{\mathrm{\nu }}\cdot {\mathbf{u}}_{\mathrm{\mu }}+{\mathrm{\nu }}_{\mathrm{\nu }0}+u_{\mathrm{\mu }0}\right)}{\sum _j\exp \left({\mathbf{v}}_{\mathbf{j}}\cdot {\mathbf{u}}_{\mathrm{\mu }}+{\mathrm{\nu }}_{j0}+u_{\mathrm{\mu }0}\right)},$$

$${\mathbf{q}}_{\mathbf{\mu }}=[p({\mathrm{\nu }}_1|\mathrm{\mu }),\dots p({\mathrm{\nu }}_M|\mathrm{\mu })]$$

Here, v_j0 + u_μ0 are row and column biases, which are required to accurately estimate the conditional probabilities. The above transformation is the softmax transform [47] to compute probabilities from real-valued quantities. This transformation is also known as the inverse clr transform [48], which enforces scale invariance as shown in the simulations. In the mmvec model’s generative process, these conditional probabilities generate the metabolite abundances y_k for a given sample k through a multinomial distribution.

$${\mathbf{y}}_{\mathbf{k}}\sim Multinomial(n,{\mathbf{q}}_{\mathbf{\mu }}),$$

where n is the total metabolite abundances across sample k. It is important to note that metabolite abundances themselves are not counts, but rather a continuous representation of molecule counts. We make the simplifying assumption that these continuous valued abundances can be approximated by Multinomial count models.

This model bears resemblance to how word2vec estimates word probabilities conditioned on a single particular word [49]. There are a couple of majors differences to be considered. First, in the original application of word2vec, a skipgram was proposed. Skipgrams [49] have been designed to account for the sequential nature of text. There is no such sequential nature with microbiome or metabolite samples, the only ordering information that is known is the sample membership. As a result, the skipgrams can be replaced using multinomial sampling, where a single microbe is randomly sampled from a microbiome sample at each gradient descent step.

Second, in the original word2vec application a single input/output word pair were evaluated at each gradient descent step, which is required to incorporate the contextual information of words within sentences. In the application of multiomics, this is unnecessasrily complicated, since there is no such contextual with regards to microbes and metabolites. Instead, all of the metabolite abundances can be simultaneously evaluated for each gradient descent step, ultimately speeding up computations. Specifically, these metabolite abundances are simultaneously considered in order to estimate the conditional probabilities q_k for the given microbial count u_jk. From these conditional probabilities, the metabolite abundances y_k are generated from a Multinomial distribution. This process is repeated across all of the microbial reads. To show that p(ν|μ) truly approximates the probability of observing a metabolite given a microbe, we first need to make the simplifying assumption that the conditional distribution of a metabolite given the presence of a single microbe also follows a multinomial distribution as follows

$$p(Y=y|X_{\mathrm{\mu }}=1)=Multinomial(y|q_{\mathrm{\mu }})$$

Where y is the vector of observed metabolites, Y is the random variable modeling metabolite abundances, X is a random variable modeling microbe abundances, x is a vector of observed microbes and μ is a single microbe. Given these modeling assumptions, we can parameterize the conditional Multinomial distributions with embedding vectors as described above. This estimation procedure can be reformulated as a matrix factorization, where the conditional probability matrix is decomposed into two weight matrices U and V, which are comprised of microbe-metabolite vectors as follows

$$\mathbf{U}={[\mathbf{0},{\mathbf{u}}_{\mathbf{0}},{\mathbf{u}}_{\mathbf{1}},\mathrm{...},{\mathbf{u}}_{\mathbf{N}}]}^T\mathbf{V}=[{\mathbf{v}}_{\mathbf{0}},\mathbf{0},{\mathbf{v}}_{\mathbf{1}},\mathrm{...},{\mathbf{v}}_{\mathbf{M}}].$$

Here U∈R^N×p and V∈R^(M−1)×p represents the corresponding embeddings for N microbes and M metabolites. The number dimensions p for both U and V as well as the priors are specified by the user, but can also be evaluated during cross-validation. The biases u₀ and v₀ are critical for estimating accurate co-occurrence probabilities, as suggested by similar methodologies used in recommender systems [50]. The U and V matrices are estimated through maximum a posteriori (MAP) estimation using ADAM [51] with the following log-posterior

$$\mathcal{L}={\mathcal{L}}_Y+{\mathcal{L}}_U+{\mathcal{L}}_V$$

$${\mathcal{L}}_U=\sum _{\mathrm{\mu }}\sum _{\mathrm{\varrho }=1}^p\mathcal{N}(U_{\mathrm{\mu },\mathrm{\varrho }}|0,{\mathrm{\sigma }}_u)$$

$${\mathcal{L}}_V=\sum _{\mathrm{\nu }}\sum _{\mathrm{\varrho }=1}^p\mathcal{N}\left(V_{\mathrm{\nu },\mathrm{\varrho }}|0,{\mathrm{\sigma }}_{\mathrm{\nu }}\right)$$

$${\mathcal{L}}_Y=\sum _k\sum _{r\in x_k}Multinomial({\mathbf{y}}_{\mathbf{k}}|{\mathbf{q}}_{\mathbf{\mu }}).$$

Within a single iteration of stochastic gradient descent a single microbial sequence i is randomly drawn and compared to a complete set of metabolite abundances y_i for that given sample. If there are a total of R microbial reads across all of the microbial samples, there will be R iterations for a complete epoch over the microbial dataset. This means that the running time of this training process is O(RM) for a single epoch. Cross validation can be performed by holding out samples measuring the predictive power by looking at the sum of squares errors. Predictions can be made as follows

$$SSE=\sum _{k,i}{\left(y_k-m_k\cdot softmax\left(\mathbf{V}{\mathbf{U}}_{u_{ik},\cdot }\right)\right)}^2.$$

Where the predictive metabolite abundances are compared to the holdout abundances y_k across all microbial reads i in the holdout samples k. m_k denotes the total metabolite abundances in sample k

10.2. Microbe-metabolite vectors in simplicial coordinates

Here, we will provide some insights behind the underlying geometry behind this neural network. Doing so will provide intuition behind the algebraic operations commonly applied in the context of word2vec, suggesting the possibility of performing similar tasks in the context of microbe-metabolite interactions. Furthermore, this will motivate the use of the Aitchison distance to quantify microbe-microbe and metabolite-metabolite interactions. Finally we will make a connection to topic modeling, providing another means to potentially interpret the latent dimensions in the model. The connection between the softmax and the inverse clr transform suggests that the inputs to this transform can be represented in clr coordinates. The softmax function and its corresponding inverse, the clr transform, is given as follows

$$softmax(x)=[\frac{e^{x_1}}{\sum _i{e}^{x_i}},\dots ,\frac{e^{x_1}}{\sum _i{e}^{x_i}}]$$

$$clr(z)=[\log \frac{z_1}{g(z)},\dots ,\log \frac{z_D}{g(z)}]$$

Since biases are incorporated into the mmvec model, by construction Q=UV^T is both row centered and column centered, meaning that the sum of rows are zero and the sum of the columns are zero. Given this the following holds

Theorem: If Q=UV and 1_NQ=0 and Q1_M=0 then U1_p=0 and V1_p=0

Suppose that there exists another solution $\mathbf{Q}=\mathbf{U}{\mathbf{V}}^{{*}^{\mathbf{T}}}$ where $\mathbf{V}=\mathbf{V}-{\mathbf{1}}_{\mathbf{M}}{\mathbf{\lambda }}_{\mathbf{v}}^{\mathbf{T}}$ and λ_v∈R^p. Then

$$\mathbf{Q}=\mathbf{U}\left(\mathbf{V}-{\mathbf{1}}_{\mathbf{M}}{\mathbf{\lambda }}_{\mathbf{v}}^{\mathbf{T}}\right).$$

Given that the rows of Q sum to 0, then

$$\mathbf{U}{\left(\mathbf{V}-{\mathbf{1}}_{\mathbf{M}}{\mathbf{\lambda }}_{\mathbf{v}}^{\mathbf{T}}\right)}^T{\mathbf{1}}_{\mathbf{M}}=0$$

$$\mathbf{U}{\mathbf{\lambda }}_{\mathbf{v}}M=0.$$

This means that only the trivial solution λ_v=0 exists, therefore the rows of V do sum to 0.

Using the same reasoning above, suppose that there exists another solution Q=U*V^T where ${\mathbf{U}}^{*}=\mathbf{U}-{\mathbf{1}}_{\mathbf{N}}{{\mathbf{\lambda }}_{\mathbf{u}}}^T$ and λ_u∈R^p. Then

$$\mathbf{Q}=\left(\mathbf{U}-{\mathbf{1}}_{\mathbf{N}}{{\mathbf{\lambda }}_{\mathbf{u}}}^T\right){\mathbf{V}}^T.$$

Given that the columns of Q sum to 0, then

$${{\mathbf{1}}_{\text{N}}}^T\left(\mathbf{U}-{\mathbf{1}}_{\text{N}}{{\mathbf{\lambda }}_{\mathbf{u}}}^T\right){\mathbf{V}}^T=0$$

$$N{{\mathbf{\lambda }}_{\mathbf{u}}}^T\mathbf{V}=0.$$

This means that only the trivial solution λ_u=0 exists, therefore the rows of U do sum to 0.

Therefore the rows of both U and V must sum to zero if U and V are non-trivial.

As noted in previous compositional data analysis work, the sum of the components within a vector in clr coordinates is zero. Given that the row vectors within U and V both sum to zero, that suggests that each of these vectors are also in clr coordinates. This means the following properties are satisfied

Topic proportions

Since the U and V row vectors are in clr coordinates, that implies that these row vectors can be directly converted to p-dimensional proportions, yielding a similar interpretation to topics used in models such as LDA [52, 53].

Linearity

Vectors in clr coordinates are known to satisfy linearity, namely

$$clr(\mathrm{\alpha }x+y)=\mathrm{\alpha }clr(x)+clr(y)$$

for α∈R, x∈S^p and y∈S^p. This linearity property was leveraged in word2vec models to perform analogy reasoning. Since both microbes and metabolites are in clr coordinates, it should be possible to categorize microbe-microbe and metabolite-metabolite interactions.

Isometry

The clr transform is distance preserving, meaning that the Aitchison distance on proportions is equivalent to the Euclidean distance on clr vectors. This provides motivation for using Euclidean distances to compute microbe-microbe and metabolite-metabolite similarities.

10.3. Visualization through biplots

Visualization techniques from compositional data analysis can aid with interpretation [54, 55]. U and V can be visualized as factors within a biplot to visualize the microbe-metabolite embeddings on a single plot. The first two latent dimensions of U represent microbial coordinates on a 2D scatter plot and the first two latent dimensions of V represent metabolite coordinates on a 2D scatter plot. Typically the coordinate from the V matrix are plotted as arrows from the origin in order to identify features that explain the variance in U. However, in our case studies, there are typically many more metabolites than microbes - so we opt to visualize the metabolites as points and microbes as arrows for a simpler visualization As suggested by the above theorem, the distance between points approximates the Aitchison distance between metabolites, and the distance between arrow tips approximates the Aitchison distance between microbes. As suggested in [56], the Aitchison distance is also equivalent to the variance of the log ratios, suggesting that microbe-microbe and metabolite-metabolite distances could also be interpreted as a measure of proportionality [23].

10.4. Benchmarks

The simulated data was based on a cystic fibrosis biofilm model derived in Quinn et al [27] shown in Figure S12 in the paper. The biofilm model was built to explain how fermenters and P. aeruginosa responded to different concentrations of sugars, amino acids, pH, oxgygen and antibiotics across the Winogradsky column. These models solved for differential equations integrating Monad kinetics and diffusion processes and was run in Matlab using the code provided at https://github.com/zhangzhongxun/WinCF_model_Code

From this simulation, we only focus 2 microbes and 5 compounds. The two microbes are P. aeroginosa (Θ_p) and fermenters (Θ_f). The five compounds (SG), acids (F), ammonium (P), amino acids (SA) and inhibition molecules (I). In order to simulate a high dimensional dataset, each microbial taxon was split into 50 different subtaxa and each compound was split into 50 molecular subclasses. The partitioning procedure is given as follows

$${\mathbf{p}}_{\mathbf{i}}\sim \mathcal{N}\left(\mathbf{0},{\mathrm{\sigma }}_o\mathbf{I}\right){\mathbf{q}}_{\mathbf{i}}\sim \mathcal{N}\left(\mathbf{0},{\mathrm{\sigma }}_c\mathbf{I}\right)$$

$${\mathbf{o}}_{\mathbf{ij}}={\mathrm{\kappa }}_{ij}il{r}^{-1}\left({\mathbf{p}}_{\mathbf{i}}\right){\mathbf{c}}_{\mathbf{ik}}={\mathrm{\eta }}_{ik}il{r}^{-1}\left({\mathbf{q}}_{\mathbf{i}}\right),$$

where p_i is a vector proportions representing how the subtaxa corresponding to j will be distributed in sample i. κ_ij represents the absolute abundance of taxon j in sample i. o_ij represents a vector of the absolute abundances for all of the subtaxa corresponding to taxon j. These are the absolute abundances that are used for comparison in Figure 2.

Here we use the ilr⁻¹ transform to generate proportions from a multivariate normal distribution. Here the multivariate normal distribution is centered around zero, and the covariance matrix σ_oI has only a constant diagonal structure with a tunable parameter σ_o specifying the variability of the partitioning procedure. Larger values of σ_o will cause the allocations of the microbes to be increasingly uneven.

The partitioning procedure is identical for the metabolites. q_i is a vector proportions representing how the subcompounds corresponding to k will be distributed in sample i. η_ik represents the absolute abundance of compound k in sample i. c_ik represents a vector of the absolute abundances for all of the subtaxa corresponding to compound k. The multivariate normal distribution used to generate the proportions is centered around zero. The covariance matrix σ_cI has only a constant diagonal structure with a tunable parameter σ_c specifying the variability of the partitioning procedure. Larger values of σ_c will cause the allocations of the metabolites to be increasingly uneven.

Once the subtaxa and subcompounds absolute abundances have been simulated, the microbial relative counts and metabolite abundances are simulated. The sampling procedure is performed as follows

$${\mathrm{\zeta }}_i\sim \mathcal{L}\mathcal{N}\left(n,{\mathrm{\tau }}_o\right){\mathrm{\omega }}_i\sim \mathcal{L}\mathcal{N}(m,{\mathrm{\tau }}_c)$$

$$x_i\sim \mathcal{P}\mathcal{L}\mathcal{N}\left({\mathrm{\zeta }}_{i}C\left({\mathbf{o}}_{\mathbf{i}}\right),{\mathrm{\epsilon }}_o\right)y_i\sim \mathcal{L}\mathcal{N}\left({\mathrm{\omega }}_{i}C\left({\mathbf{c}}_{\mathbf{i}}\right),{\mathrm{\epsilon }}_c\right).$$

The total sequencing depths and total intensities for sample i are draw from Lognormal distributions with means parameterized by n and m and overdispersion parameters τ_o and τ_c. We chose to use the lognormal distribution for three reasons. First, the lognormal distribution models overdispersion. Second, the lognormal distribution has a simpler interpretation than other overdispersed distributions such as the negative binomial, since the parameters can be directly interpreted as a normal distribution and consequentially has a compositional interpretation due to its connection to the ilr transform. Finally, the lognormal distribution commonly used for modeling in the the ecological literature in the context of studying species populations in Niche theory and Neutral theory, leading to a natural biological interpretation.

Once the total sequencing depth and the total intensities are sampled, the microbial sequencing counts and metabolite abundances are then sampled. A Poisson lognormal distribution is used to generate the microbial counts from the microbial proportions C(o_i) scaled by the sequencing depth ζ_i. The counts are sampled with error ε_o. A Lognormal distribution is used to generate the metabolite abundances from metabolite proportions C(c_i) scaled by the total intensity ω_i. The abundances are sampled with error ε_c. All of the code used to generate the benchmarks can be found at https://github.com/knightlab-analyses/multiomic-cooccurrences.

10.5. Software workflows

To facilitate utilization of the mmvec tool, we have developed two different user facing interfaces. First, we have developed a qiime2 plugin [57], where mmvec can be run using a simple command line interface. This interface is complemented using [26], where users can monitor convergence rates for their models in real-time and evaluate how different parameters will affect their model fit (Figure S4). Second, we have integrated mmvec into the Global Natural Product Social Molecular Networking (GNPS) platform that can be accessed by the public. The online interface through GNPS resolves several usability issues. First, GNPS facilitates import of metabolomics data into qiime2 by pre-processing, importing, and sample renaming, This is performed as part of the standard metabolomics analysis at GNPS (e.g. molecular networking and feature-based molecular networking). Second, since it is possible to both download and re-use outputs of workflows run at GNPS directly, it is straightforward to select the GNPS qza and molecule annotations needed for mmvec. The user will need to upload the accompanying feature and taxonomy data for qiime2 and the analysis will be begin. Once the workflow completes, the biplots can be viewed directly in the browser and other outputs (e.g. ranks) are available for download (Figure S5).

The mmvec implementation is written using Tensorflow and can leverage GPUs for computation. The number of gradient descent iterations is specified by the user and model fit diagnostics can be monitored in real time using Tensorboard. The runtime of mmvec across 16 cores can take multiple days until a model convergence reaches convergence. With GPUs, the running time is reduced to a few hours. Using a Telsa GPU, the model can reach convergence within 4 hours on the IBD dataset comprised of 562 microbial taxa, 26,966 metabolite features and 400 samples. However, there is a trade-off of accuracy and running time. More accurate models require smaller learning rates and may take longer to run.

10.6. Data Analysis

Due to the overwhelming sparsity in microbiome datasets, some filtering is required in order to infer microbe-metabolite interactions. We chose to filter out microbes that appear in less than 10 samples, since these microbes don’t have enough information to infer which metabolites are co-occurring with them. In other words the mmvec model has too many degrees of freedom to perform inference on these microbes. For the cystic fibrosis study, there were 172 samples and after filtering there were 138 unique microbial taxa and 462 metabolite features. For the biocrust soils study, there were 19 samples and after filtering there were 466 unique microbial taxa and 85 metabolite features. For the murine high fat diet study, there were 434 samples and after filtering there were 902 microbes and 11978 metabolites. For the IBD dataset, there were 13920 features in the c18 LCMS dataset, 26966 features in the c8 LCMS dataset and 562 taxa. Cross validation was performed across all studies to evaluate overfitting. In the desert biocrust soils experiment, 1 sample out of 19 samples was randomly chosen to be left out for cross-validation. In all of the other studies, 10 samples were randomly chosen to be left out for cross-validation. All of the analyses can be found under https://github.com/knightlab-analyses/multiomic-cooccurences.

10.7. Data availability

The cystic fibrosis sequencing and metadata data can be found under http://qiita.microbio.me; study id: 10863. The corresponding GNPS analysis can be accessed at http://gnps.ucsd.edu/ProteoSAFe/status.jsp?task=34d825dbf4e9466e81d809faf814995b.

The biocrust soils data was retrieved from the supplemental section in Swenson et al [30]. The High fat diet murine model case study 16S rRNA data can be found under http://qiita.microbio.me; study id: 10856. The High fat diet murine model case study are publicly available at https://massive.ucsd.edu/ at MassIVE ID MSV000080918. The GNPS analysis for this study can be accessed at https://gnps.ucsd.edu/ProteoSAFe/status.jsp?task=977d85bba47b4e96bf69872b961b8edd

The IBD data used can be found under https://ibdmdb.org.

See Life Sciences Reporting Summary for more details on the experimental design.

10.7. Software availability

The software implementing the mmvec algorithm can be found under https://github.com/biocore/mmvec.

Differential abundance analyses in the high fat diet study was performed using L2-regularized multinomial regression using software available at https://github.com/biocore/songbird

The software used to build the multiomics network can be found at https://github.com/mortonjt/multiomics_network.

Biplots were generated using Emperor [58].