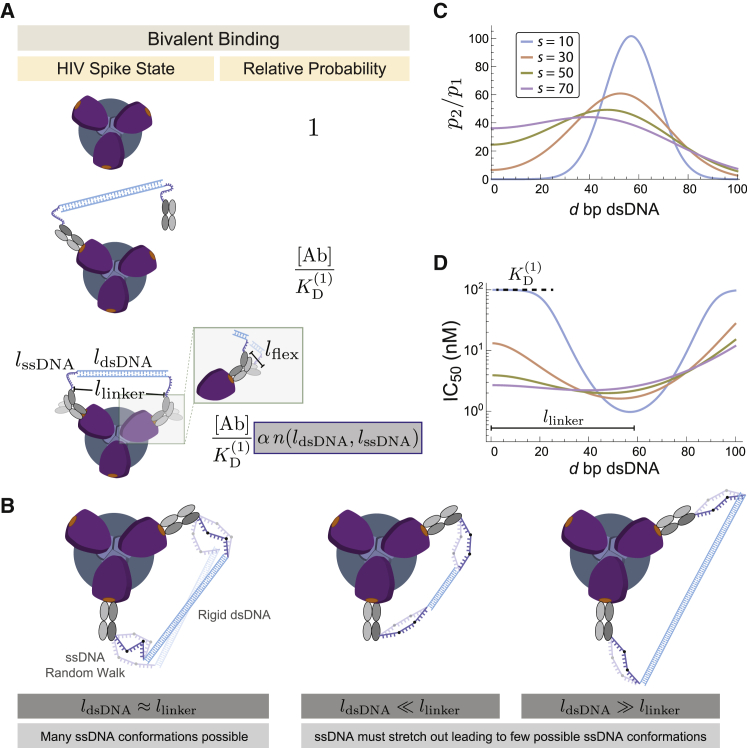
Figure 2.

Modeling the Optimal Linker Length for a diFab

(A) The energetic and entropic costs of monovalent binding depend upon the concentration [Ab] and dissociation constant $K_{\text{D}}^{\left(1\right)}$ of a single Fab binding. The boost in bivalent binding is dictated by the geometric or avidity factors $\alpha$ (which is the same for all diFabs) and $n$ (which depends upon the length of the dsDNA and ssDNA, the optimal length $l_{\text{linker}}$ of the linker between two bound Fabs, and the flexibility $l_{\text{flex}}$ between the C_H1-C_L and V_H-V_L domains of a bound Fab). The ability to neutralize is given by the sum of relative probabilities for the monovalent and bivalent states divided by the sum over all states.

(B) The boost $\alpha n$ of bivalently binding is computed by treating the ssDNA as a random walk and the dsDNA as a rigid rod (see STAR Methods section titled “Number of Microstates in the Model Including ssDNA”). An optimal linker matches the length of the dsDNA to the length between two bound Fabs $\left({\mathit{l}}_{\text{dsDNA}}\approx {\mathit{l}}_{\text{linker}}\right)$, giving rise to many configurations for the bivalently bound state and increasing its likelihood.

(C and D) The relative probability that a diFab with d bp dsDNA and s bases ssDNA is bivalently (p₂) versus monovalently (p₁) bound (C) and the predicted IC₅₀ values for these same constructs (D). Parameters used were l_linker = 20 nm, l_flex = 1 nm, $\mathit{\alpha }=5\times {10}^6$, and ${\text{K}}_{\text{D}}^{\left(1\right)}=100\text{nM}$.