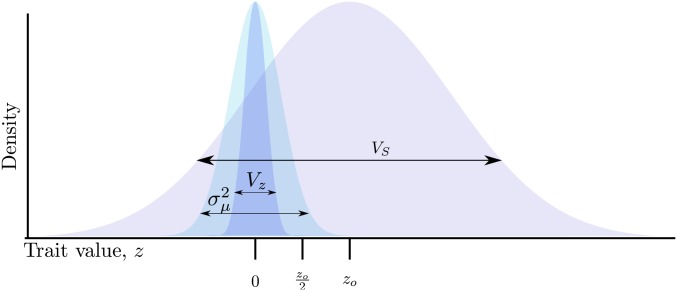
Figure 1.

Schematic of the model. A Wright–Fisher population evolves to equilibrium around an optimum trait under Gaussian stabilizing selection with mean zero, where the parameter $V_S$ represents the intensity of selection against extreme trait values $\left(w=e^{-z^2/2V_S}\right)$. At equilibrium, the mean trait value is $\overline{z}\approx 0$ and the genetic variance $V_G$ equals the phenotypic variance $V_z$. Mutations arise at a constant rate with effect sizes, γ, drawn from a Gaussian distribution with mean zero and variance ${\sigma }_{\gamma }^2$. The optimum then shifts to $z_o>0$, such that $w=e^{-{\left(z-z_o\right)}^2/2V_S}$. During adaptation, $\overline{z}$ approaches $z_o$ due to allele frequency change and new mutations. At any point during adaptation, mutations with effect sizes $\gamma >\left(z_o-\overline{z}\right)/2$ will overshoot the optimum if they reach high frequency or fix.