Fig. 3.

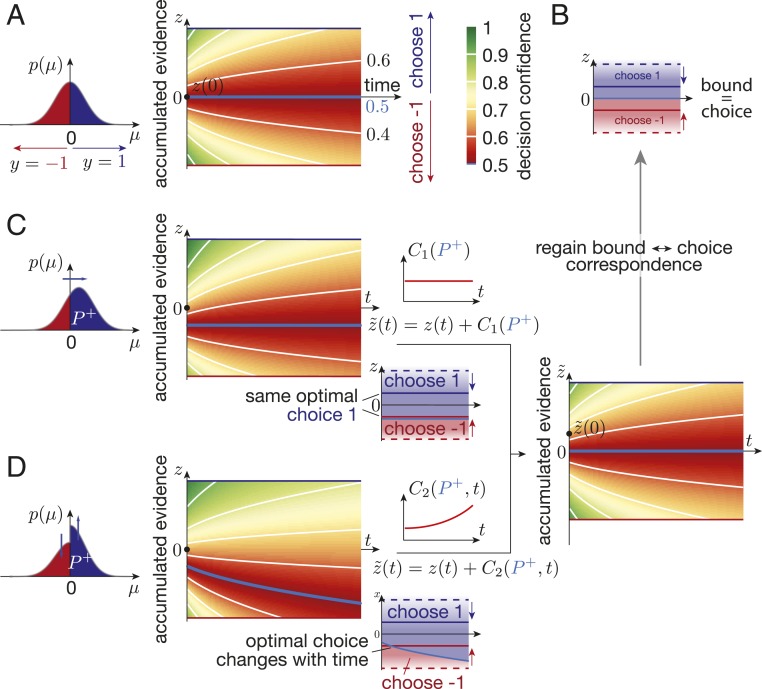
Decision confidence, prior biases, and the relation between decision boundary and choice. (A) For an unbiased prior [i.e., $P^{+}\equiv p\left(\mu \ge 0\right)=1/2$], the decision confidence (color gradient) is symmetric around $z=0$ for each fixed time $t$. The associated posterior belief $p\left(\mu \ge 0|z\left(t\right),t\right)$ (numbers above/below “time” axis label; constant along white lines; $\mathrm{½}$ along light blue line) promote choosing $y=1$ and $y=-1$ above (blue area in B) and below (red area in B) $z=0$. (B) As a result, different choices are Bayes-optimal at the blue/red decision boundaries, as long as they are separated by $z=0$, irrespective of the boundary separation (solid vs. dashed blue red lines). (C) If the prior is biased by an overall shift, the decision confidence is countershifted by the same constant across all $t$. In this case, both decision boundaries might promote the same choice, which can be counteracted by a time-invariant shift of $z$ by $C_1\left(P^{+}\right)$. (D) If the prior is biased by boosting one side while suppressing the other, the decision confidence shift becomes time dependent, such that the optimal choice at a time-invariant boundary might change over time. Counteracting this effect requires a time-dependent shift of $z$ by $C_2\left(P^{+},t\right)$. In both C and B, we have chosen $P^{+}=0.6$, for illustration.