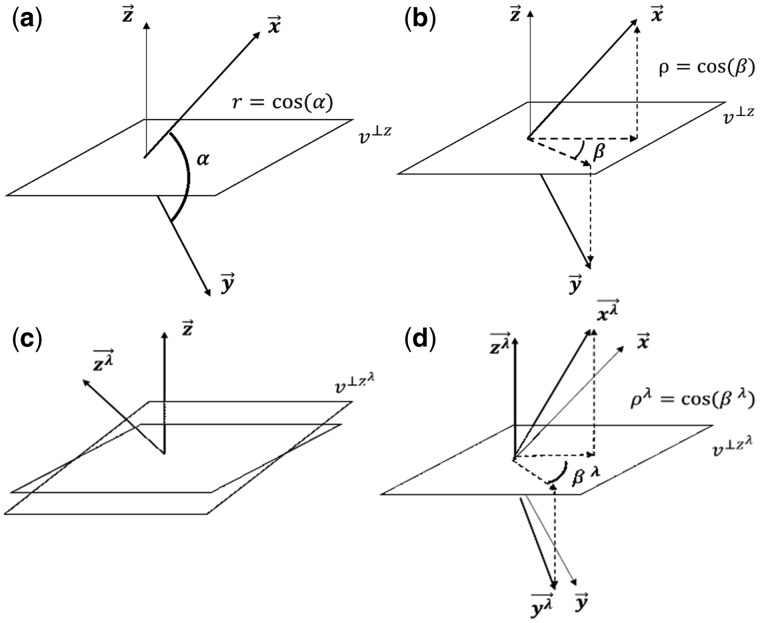
Fig. 1.

Geometry of the partial correlation. The vectors ${\displaystyle \overrightarrow{\mathit{x}}}$, ${\displaystyle \overrightarrow{\mathit{y}}}$ and ${\displaystyle \overrightarrow{\mathit{z}}}$ represent the random variables X, Y and Z  in subject space. In Panel (a), the correlation $\mathit{r}$ between X and Y is the cosine of $\alpha$. In Panel (b), the partial correlation between X and Y can be interpreted as the cosine of the angle $\beta$. That is the cosine between the projection of ${\displaystyle \overrightarrow{\mathit{x}}}$ and ${\displaystyle \overrightarrow{\mathit{y}}}$ onto a plane orthogonal to ${\displaystyle \overrightarrow{\mathit{z}}}$. The shrinkage effect consists in that the vectors ${\displaystyle \overrightarrow{\mathit{x}}}$, ${\displaystyle \overrightarrow{\mathit{y}}}$ and ${\displaystyle \overrightarrow{\mathit{z}}}$are transformed to ${\displaystyle \overrightarrow{{\mathit{x}}^{\mathit{\lambda }}}}, {\displaystyle \overrightarrow{{\mathit{y}}^{\mathit{\lambda }}}}$ and ${\displaystyle \overrightarrow{{\mathit{z}}^{\mathit{\lambda }}}}$ such that their lengths remain 1, and only the angles between each other change. In other words, the transformed vectors become less correlated. In Panel (c), the geometrical effect of the shrinkage consists in changing the projection plane ${\mathit{v}}^{\perp \mathit{z}}$ to ${\mathit{v}}^{\perp {\mathit{z}}^{\mathit{\lambda }}}$. In Panel (d), the ‘shrunk’ partial correlation ${\rho }^{\lambda }$ between X and Y is the cosine of the angle ${\beta }^{\lambda }$. That is the cosine between the projections of ${\displaystyle \overrightarrow{{\mathit{x}}^{\mathit{\lambda }}}}$ and ${\displaystyle \overrightarrow{{\mathit{y}}^{\mathit{\lambda }}}}$ onto ${\mathit{v}}^{\perp {\mathit{z}}^{\mathit{\lambda }}}$