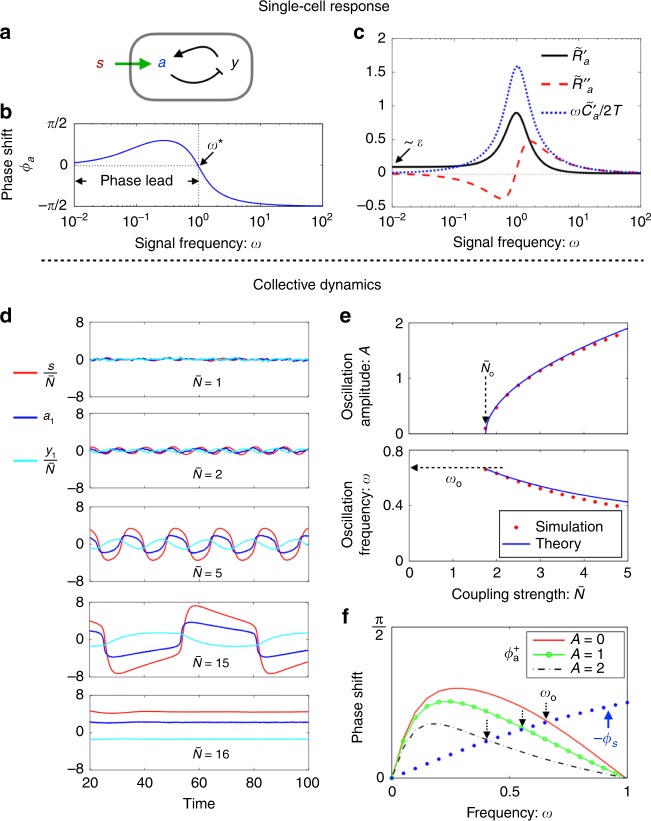
Fig. 3. A weakly nonlinear model with adaptation.

a–c Single-cell response. a A noisy two-component model with negative feedback. b Frequency-resolved phase shift ${\varphi }_a=-\arg \left({\tilde{R}}_a\right)$. A sign change takes place at $\omega ={\omega }^{*}\simeq {\left({\tau }_a{\tau }_y\right)}^{-1∕2}$, with $a$ leading $s$ on the low frequency side. c Real (${\tilde{R}}_a^{\prime }$) and imaginary (${\tilde{R}}_a^{″}$) components of the response spectrum. ${\tilde{R}}_a^{\prime }$ is of order $ϵ$ in the zero frequency limit, while ${\tilde{R}}_a^{″}$ changes sign at $\omega ={\omega }^{*}$. Also shown is the correlation spectrum ${\tilde{C}}_a\left(\omega \right)$ multiplied by $\omega ∕\left(2T\right)$, where $T$ is the noise strength. The fluctuation-dissipation theorem ${\tilde{R}}_a^{″}=\omega {\tilde{C}}_a\left(\omega \right)∕\left(2T\right)$ for thermal equilibrium systems is satisfied on the high frequency side, but violated at low frequencies. d–f Simulations of coupled adaptive circuits. d Time traces of the signal (red) and of the activity (blue) and memory (cyan) from one of the participating cells at various values of the coupling strength $\overline{N}={\alpha }_1{\alpha }_{2}N$. e The oscillation amplitude $A$ (of activity $a$) and frequency $\omega$ against $\overline{N}$. The amplitude $A$ grows as ${\left(\overline{N}-{\overline{N}}_{\mathrm{o}}\right)}^{1∕2}$ here, a signature of Hopf bifurcation. f Determination of oscillation frequency from the renormalised phase matching condition at finite oscillation amplitudes: ${\varphi }_a^{+}\left(\omega ,A\right)=-{\varphi }_s^{+}\left(\omega ,A\right)$. The linear model for $s$ yields ${\varphi }_s^{+}\left(\omega ,A\right)=-{\varphi }_s\left(\omega \right)$. Parameters: ${\tau }_a={\tau }_y=\gamma =K=c_3=1$, ${\alpha }_1={\alpha }_2=0.5$, and $ϵ=0.1$. The strength of noise terms is set at $T=0.01$.