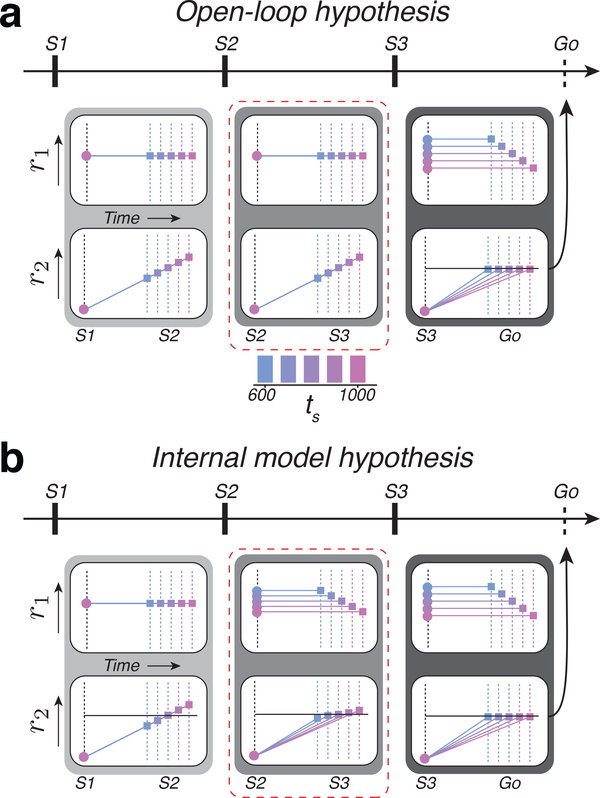
Figure 2. Predictions of the open-loop and internal model hypothesis in the 1-2-3-Go task.

a) Activity profile of two hypothetical populations, r₁ and r₂, under the open-loop hypothesis. Predictions are shown for each of the three epochs. r₁ provides the clock and r₂ integrates the clock to track elapsed time. During both the first and second epochs (light and medium gray boxes), the clock signal is independent of t_s. Therefore, r₂ at S2 or S3 represent the measured interval (different colored squares). These measurements set the clock speed (output of r₁) according to t_e(S3), and, as a consequence, r₂ ramps to threshold (horizontal black line) at a rate that depends on t_s from S3 to Go (dark gray box). b) Activity profile under the internal model hypothesis. r₁ and r₂ represent the control signal and simulation, respectively. During the first epoch (light gray box), the r₁ population supplies a constant speed command according to the mean of the prior. The r₂ population integrates this speed command and produces ramping activity that terminates at different points depending on the sample interval, t_s (different colored squares). The difference between the terminal point of r₂ and the predicted terminal point based on the mean of the prior (horizontal line) provides an error that allows r₁ to encode an interval-dependent speed command in the subsequent epoch (medium gray box, top). The corresponding r₂ population integrates the updated speed to generate ramping activity whose slope varies with t_s (bottom). The same process is repeated in the third epoch (dark gray box). Dashed red line highlights the key differences between the two hypotheses.