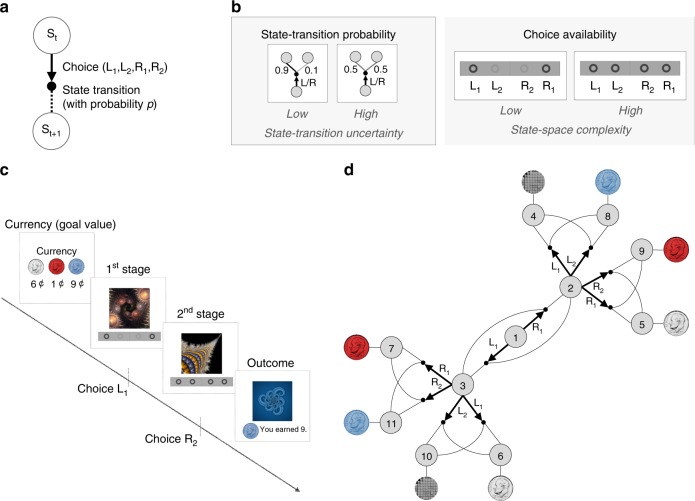
Fig. 1. Task design.
a Two-stage Markov decision task. Participants choose between two to four options, followed by a transition according to a certain state-transition probability p, resulting in participants moving from one state to the other. The probability of successful transitions to a desired state is proportional to the estimation accuracy of the state-transition probability, and it is constrained by the entropy of the true probability distribution of the state-transition. For example, the probability of a successful transition to a desired state cannot exceed 0.5 if p=(0.5, 0.5) (the highest entropy case). b Illustration of experimental conditions. (Left box) A low and high state-transition uncertainty condition corresponds to the state-transition probability p = (0.9, 0.1) and (0.5, 0.5), respectively. (Right box) The low and high state-space complexity condition corresponds to the case where two and four choices are available, respectively. In the first state, only two choices are always available, in the following state, two or four options are available depending on the complexity condition. c Participants make two sequential choices in order to obtain different colored tokens (silver, blue, and red) whose values change over trials. On each trial, participants are informed of the “currency”, i.e. the current values of each token. In each of the subsequent two states (represented by fractal images), they make a choice by pressing one of available buttons (L1, L2, R1, R2). Choice availability information is shown at the bottom of the screen; bold and light gray circles indicate available and unavailable choices, respectively. d Illustration of the task. Each gray circle indicates a state. Bold arrows and lines indicate participants’ choices and subsequent state-transition according to the state-transition probability, respectively. Each outcome state (state 4–11) is associated with a reward (colored tokens or no token represented by a gray mosaic image). The reward probability is 0.8.