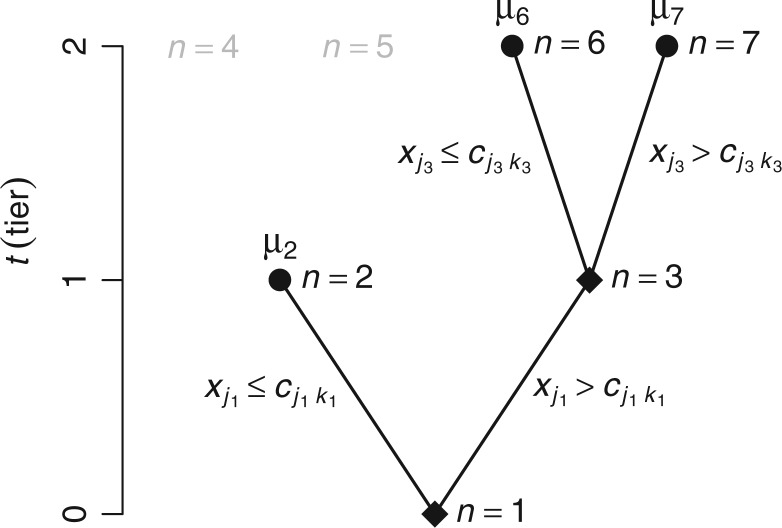
Fig. 1.
This is a diagram of a binary regression tree. On the vertical axis, we have the tier,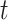 
, i.e., in each tier, we may have nodes 
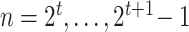. This tree has branch decisions (diamonds) at nodes 
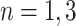and terminal leaf nodes (circles) at 
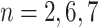with corresponding output values of 
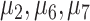. At branches 
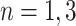, the splitting variable is 
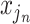and the cutpoint is 
, i.e., if 
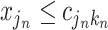, then go to node 
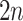, otherwise, 
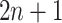. Note that nodes 
(in gray) do not appear since node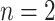 
is a leaf. This tree is denoted by 
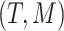and a corresponding regression function 
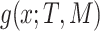where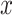 
is a vector of covariates, 
. 
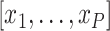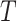represent the branch decision rules of the form 
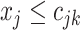and is composed of ordered triples, 
: 
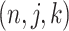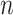for the node, 
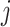for covariate 
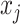and 
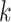for the cutpoint 
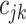. So, here we have 
. 
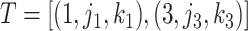represents leaves and is composed of ordered pairs,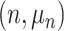 
: 
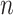for the node and 
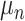for the outcome value. So, 
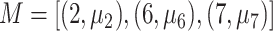. The regression function, 
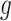, climbs the tree. For example, suppose 
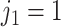and 
, then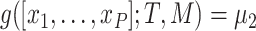 
.