Fig. 2.

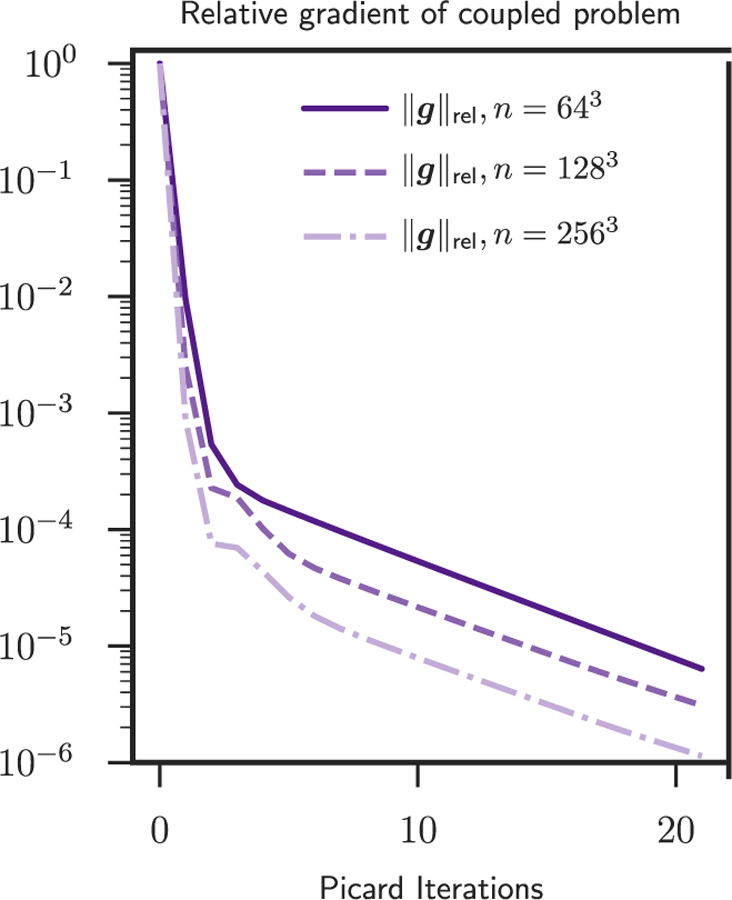
Here we summarize the norm of the reduced gradient of (3) as a function of the Picard iteration number for the sinusoidal analytic tumor / analytic velocity (SIN) test case. The exact numbers are reported in Table 3. The tree different curves correspond to the three different spatial resolutions for the velocity and tumor parameters. We use N_i ∈ {64, 128, 256} points per dimension for the velocity and analogously p ∈ {8, 64, 512}. We perform 20 Picard iterations after termination of the parameter-continuation scheme for the regularization parameter of the registration solver. We have two observations. First, the convergence of our scheme does not deteriorate as we increase the mesh resolution. As we refine the mesh we can reduce the gradient further and the number of iterations does not deteriorate (as it would be the case for a steepest descent method). Second, the convergence of our scheme eventually slows down for all mesh sizes.