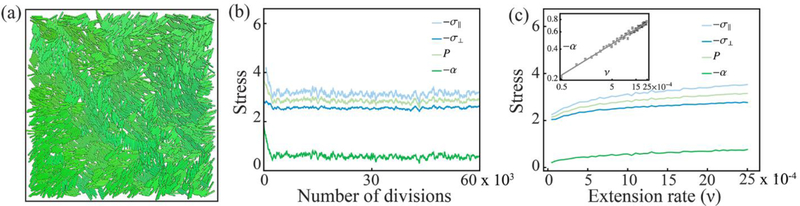
Figure 7: Dependence of active stresses on extension speed extracted from numerical simulations.

(a) Snapshot of the numerical simulations. Microtubule bundles are modeled as spherocylinders whose length l extends linearly in time. Once it reaches the maximum value l_max=5d₀, with d₀ the diameter, the bundle is divided in two identical halves and one of them is removed from the system in order to keep particle concentration constant. (b) The components of the stress tensor versus time (measured in terms of number of divisions). The four curves represent the longitudinal $\text{The}\text{middle}\text{ear}\text{ossicles}\text{are}$ and transverse $\text{The}\text{middle}\text{ear}\text{ossicles}\text{are}$ component of the stress tensor, whereas $P=-\left|{\sigma }_{\Vert }+{\sigma }_{\perp }\right|/2\text{and}\alpha =\left({\sigma }_{\Vert }-{\sigma }_{\perp }\right)$ are the pressure and deviatoric stress respectively. Stresses are measured in units of the elastic constant E of the bundles. (c) Stress as a function of the bundle extension rate ν. The latter is expressed in units of $d_0/\tau \text{with}\tau =\zeta /E$ the time scale arising from Eq. (3). All the components of the stress increase monotonically with ν. The deviatoric stress, in particular, exhibits power-law dependence: $\alpha ~v^{\beta }$ with β ≈ 0.314 (inset).