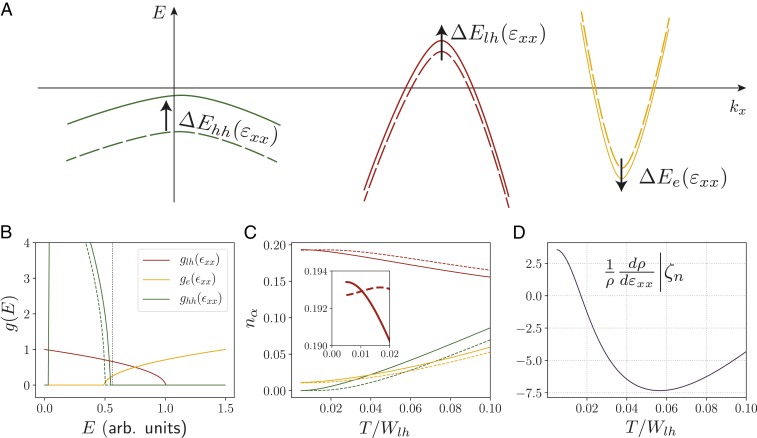
Fig. 4.

Theoretical low-energy model analysis. (A) Schematics of electron and hole pockets in the low-energy three-band model before (dashed) and after (solid) application of compressive strain. Direction of strain-induced band shifts $\mathrm{\Delta }E\left({\epsilon }_{xx}\right)$ were taken from DFT calculations (Fig. 3). (B) Density of states $g\left(E\right)$ of three-band model before (dashed) and after (solid) rigid band shifts $\mathrm{\Delta }{E}_e=-4\times 10^{-3}$ and $\mathrm{\Delta }{E}_{\text{hh}}=4\times 10^{-2}$. All energies are in units of the light-hole bandwidth $W_{lh}$. The shift ratio $\mathrm{\Delta }{E}_{hh}/\mathrm{\Delta }{E}_e=10$ is taken to be 5 times larger than the one found within DFT (see SI Appendix for a detailed discussion). Bandwidths are set to $W_e=W_{lh}=1$ and $W_{hh}=0.5$. Effective masses are assumed to be strain-independent for simplicity, and their ratios were set to $m_e*/m_{lh}*=1$ and $m_{hh}*/m_{lh}*=4.6$, which approximately agrees with SdH oscillation analysis (SI Appendix). The bottoms of the bands are at $E_{lh}^{\text{min}}=E_{hh}^{\text{min}}=0$ and $E_e^{\text{min}}=0.5$. The chemical potential $\mu \left(T=0\right)=0.56\hspace{0.17em}{W}_{lh}$ is indicated by the vertical dotted line (total electronic filling $\mathcal{N}=0.77$). (C) Carrier densities of the different bands $n_{\alpha }$ as a function of temperature $T$ for 0 and finite strain. Colors and line styles are identical to A and B. C, Inset shows that $n_{lh}$ increases at low $T$ [as long as $|E_{hh}\left({\epsilon }_{xx}\right)-\mu |\ll T$], but decreases at higher $T$, eventually causing the sign change of the ER. (D) Elastoresistivity contribution that arises from redistribution of carriers due to rigid band shifts $\mathrm{\Delta }E\left({\epsilon }_{xx}\right)$ is shown in B. We have assumed that these band shifts are caused by strain of size ${\epsilon }_{xx}=-0.2\%$. Comparison with DFT yields that $\mathrm{\Delta }{E}_{hh}=0.04W_{lh}\simeq 16\hspace{0.17em}\text{meV}$ (relative shift to the $lh$ pocket) and, thus, $T=0.06W_{lh}\simeq 300$ K. At $T=0$, $ER>0$ as electrons move from the $lh$ to the $e$ band, increasing the total number of carriers (C, Inset). At $T>0$ (or, more specifically, $T\gtrsim |E_{hh}-\mu |$), the $hh$ band is only partially filled, and moving it closer to the chemical potential shifts hole carriers from $lh$ to the $hh$ pocket, where their contribution to the conductivity is smaller. We note that the total ER also contains a contribution from the strain-induced increase of the effective masses, which leads to an approximately $T$-independent negative shift of ER.