Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Dec 11;4(26):21883–21890. doi: 10.1021/acsomega.9b02866

Macroscopic Modeling of Water Uptake Behavior of PEDOT:PSS Films

Lyazzat Zhanshayeva 1, Valentina Favaron 1, Gilles Lubineau 1,*
PMCID: PMC6933586  PMID: 31891066

Abstract

graphic file with name ao9b02866_0007.jpg

Poly(3,4-ethylene dioxythiophene)-poly(styrene sulfonate) (PEDOT:PSS) is a widely used conductive polymer (CP) for applications in electronic devices. In the context of transparent electrodes or soft actuators, the uptake of water by PEDOT:PSS is an essential element in the performance of the physical system. We study the water uptake of pure films and films treated with ethylene glycol (EG) commonly used to enhance the electrical properties of PEDOT:PSS. Gravimetric analysis was used to investigate the water sorption–desorption of PEDOT:PSS and its change with the EG treatment for a wide range of configurations (thickness, temperature, and relative humidity). We demonstrate that a simple Fickian model cannot correctly represent the experimental results; we therefore introduce a fully coupled reaction–diffusion scheme. This model describes the transport of diffusing molecules into the polymer film, taking into account, in addition to the classical diffusion mechanism, the reaction between the reactive sites of the polymer network and the water molecules. We demonstrate that solvent treatments have a direct influence on the kinetics of the water uptake of PEDOT:PSS films in terms of diffusivity, solubility, and rate of reaction. The proposed model can be used to accurately predict the water uptake of CP films in the case of complex three-dimensional configurations that are needed for the design of complex actuators.

Introduction

Because of their lightweight, flexibility, and ease of processability, organic conductive polymers (CPs) are widely applied in electronic devices.1 The most successful polymer is poly(3,4-ethylenedioxythiophene)-poly(styrene sulfonate) (PEDOT:PSS). Its tunable electrical properties (conductivity can reach 4000 S/cm by using proper treatment2−4), low-voltage-driven actuation mechanism,5 and the recently revealed self-healing effect6 make PEDOT:PSS a good candidate for transparent electrodes, organic solar cells, organic light-emitting diodes, wearable textiles, artificial muscles, sensors, and actuators.1,5,7−10

PEDOT:PSS features a strong coupling among its chemical, mechanical, and electrical behaviors, which has resulted in many applications in the field of electromechanical actuators.11 The mechanism of actuation comes from the hygroscopic nature of PSS that very easily absorbs water from the environment. Water molecules can actually exist in very different configurations. As shown by ref (12), based on the observation of isosteric heat of sorption, water molecules will mainly be adsorbed on the hydrophilic sulfonic acid groups at a low sorption degree. At a higher sorption degree, the active sites are totally saturated and water is in a free-water configuration. The absorbed water molecules increase the distance between the PEDOT:PSS grains, causing a volume increase. When an electric current is applied, the Joule effect results in the generation of in-the-volume heat, consequently changing the temperature. It results in the release of the previously absorbed water molecules, which translates into geometrical shrinking at the macroscale. PEDOT:PSS-based actuators can be operated under low voltages (0–10 V) that makes them particularly appealing for wearable electronic applications.5

Considering the phenomenology described above, water content plays a major role in PEDOT:PSS actuation properties. This phenomenology has been well studied for other families of CPs such as polypyrrole, with the pioneering work of Okuzaki’s group,13−15 but still additional data are needed in case of PEDOT:PSS. More generally, all properties of PEDOT:PSS are highly dependent on its water content. A decrease in Young’s modulus, along with an increase in the relative humidity (RH) of the environment, was reported in previous studies.16 This happens because of the weakened hydrogen bonding between the PEDOT and PSS grains, during the water uptake of hygroscopic PSS. In addition, water molecules increase the distance between PEDOT oligomers, resulting in an increase of electrical resistivity.17 A change in the distribution of both stress and strain was also observed.16 These results illustrate the crucial role of the water sorption mechanism of PEDOT:PSS in modifying the complete behavior of the film. Today, the phenomenological aspects of the PEDOT:PSS actuation and water sorption are well known. The amount of water vapor sorption decreases with an increase in temperature and hysteresis between the sorption and desorption isotherms that were previously reported,11 and there is a good understanding of the sorption isotherms from the thermodynamic viewpoint. Interesting works have been done recently, investigating the effect of microstructure (and especially the PEDOT:PSS ratio) on the coupling among water sorption, swelling, and electrical properties.18 However, to the best of our knowledge, there is no model or systematic data to describe the interplay among water absorption, mechanical expansion, and electrical stimulus. Elucidating the role of each component in the actuation properties is needed to further optimize and tailor soft actuators based on such materials.

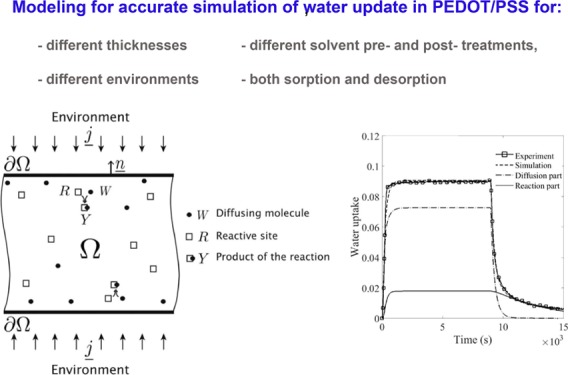
The objective of this paper is to provide a reliable macroscopic modeling of the water uptake in PEDOT:PSS films that can be used to better design transparent PEDOT:PSS electronics or actuators. To do so, we explore a wide range of experimental conditions, both during the sorption and desorption tests in order for our set of data to discriminate between the different modeling approaches.

We first used gravimetric analysis to understand the absorption–desorption mechanism by monitoring the water uptake of the film at a macroscopic level. The obtained data clearly show that a simple Fickian model presents severe limitations; we therefore need a more complex modeling approach. We decide to adopt the reaction–diffusion scheme proposed by El Yagoubi et al.19 to model the water uptake behavior. This model takes into account the reaction between water molecules and the substrate, in addition to the classical diffusion. Finally, we discuss how the constitutive parameters of this model are modified when classical treatments, such as pretreatment or post-treatment with ethylene glycol (EG), are used.

Materials and Methods

Material Preparation

An aqueous PEDOT:PSS dispersion (Clevios PH1000) was purchased from HC Starck, Inc. PH1000 was chosen because of its high electrical conductivity in comparison to other commercially available grades. It has a 1:2.5 w/w ratio of PEDOT to PSS. We study three types of films: pure, pretreated, and post-treated PEDOT:PSS. For each configuration, a drop-casting technique was used to prepare the films. A square Petri dish of size 8.5 cm × 8.5 cm, covered with a Teflon paper, was plasma-treated to remove the impurities and to maximize wettability. An Expanded Plasma Cleaner PDC-001 from Harrick Plasma was used at high power and 400 mTorr pressure, for 5 min. An adequate amount of the dispersion was then poured into the dish and cured in a fume hood for 48 h, at room temperature.

The pretreatment process was performed by adding the solvent EG (3 wt %) to the aqueous PEDOT:PSS dispersion. The solution was mixed for 6 h in a fume hood.

The post-treatment process was performed on a pure PEDOT:PSS film. The pure PEDOT:PSS film samples were placed inside a beaker filled with EG for 6 h and then removed.

The pretreated and post-treated films were annealed at 120 °C for 2 h. Let us note that we use “pretreated” and “post-treated” for naming samples after EG addition or EG rinsing and that we do not refer to oxidation/reduction of the CP. Three sample thicknesses (2L) were considered for pure films: 2L = 15 μm, 2L = 50 μm, and 2L = 100 μm, whereas only 50 μm was used for pretreated and post-treated films. The choice of relatively large thicknesses is motivated by applications on soft robotics and soft actuators, for which thicknesses are usually much larger compared to the films used for transparent electrodes. Film thicknesses were measured using a digital micrometer with a 1 μm accuracy. The drop-casting method is known for the ease of film preparation, but this method makes it difficult to control the film thickness and uniformity. Therefore, there was a 10% variation of thickness in polymer film samples. For this reason, the thickness of each individual sample was measured after processing, in order to secure accurate data.

Gravimetric Test

For gravimetric measurements, dried polymer films were cut into 7 mm by 7 mm squares using a CO2 universal laser system PLS 6.75. The following laser settings were used: speed: 5.0%; pulses per inch: 750; Z-axis: 4.00 mm; and power: 0.5, 1.5, and 2%, depending on the thickness of the film.

An IGAsorp dynamic vapor sorption (DVS) analyzer (Hiden Isochema) was used for gravimetric measurements. The temperature and RH, within the isolated chamber, were controlled while monitoring the mass uptake of the specimen with an embedded 10 μg resolution microbalance. The polymer samples were placed on a suspended stainless steel mesh inside the chamber, in order for both sides of the film to be exposed to the environment. Three configurations of the material were considered: pure, pretreated, and post-treated PEDOT:PSS. For each configuration, different samples were tested at different temperatures (26, 37, 50, and 80 °C) and RH’s (30, 60, and 80%), making a total of 36 different configurations. For each configuration, both the absorption and desorption responses were investigated. Each test was repeated three times.

We performed a systematic conditioning of the film: the water content of the film was removed prior to humidity exposure by drying the sample inside the equipment until the mass equilibrium was reached. The dried polymer films were exposed to a flow of 250 mL/min moist air until stabilization, followed by a desorption test, by keeping the temperature constant but prescribing the humidity level to 0%. The gas environment was controlled by mixing wet air with a dry flow of nitrogen. The DVS analyzer allowed the measurement of the mass uptake, m(t), every 20 s, which is a relatively high rate.

The results from the gravimetric tests were plotted as a ratio of the mass of absorbed water by the PEDOT:PSS film, Δm, to the mass of the dry sample, m0, defined as relative water uptake

graphic file with name ao9b02866_m001.jpg 1

where

graphic file with name ao9b02866_m002.jpg 2

Numerical Implementation

Gravimetric tests were reproduced using the COMSOL Multiphysics 5.2 software in which we implemented the model described briefly in the section and completely in the Supporting Information. Assuming that the thickness of the polymer film is much less than its width and length, a one-dimensional simulation was conducted. Considering the symmetry of the film, half of the thickness (L) was analyzed. The RH values were taken directly from the results file of the DVS chamber, for all configurations, to reproduce a real environment.

The mass uptake was derived, considering both the free (w) and bonded water (Y)

graphic file with name ao9b02866_m003.jpg 3

where MH2O = 0.018 kg/mol is the molar mass of water, ρ0 = 1350 kg m–3 is the initial density, and V0 is the initial volume of the sample.

The simulation and experimental curves were compared using a MATLAB Optimization Toolbox function “lsqnonlin”, which solves nonlinear least-squares data-fitting problems. The seven parameters of the model (S0, S1, D0, D1, kh, kr, and R0; see Supporting Information) were optimized. “lsqnonlin” minimizes the sum of squares of the vector-valued function, which is the difference between the experimental and simulation data. Also, the initial value of the function and its lower and upper bounds were specified individually, for each parameter. Iteration terminates when the solver reaches the stopping criteria specified by the user. For this problem, stopping criteria were the tolerance of the function value (1 × 10–8) and the number of maximum iterations (500). Each curve was optimized separately, and the parameters found for the first simulated curve were used as initial values for the next curves.

Results

Here, we only discuss raw experimental results without introducing any modeling consideration or opinion, which we will do in the Discussion section.

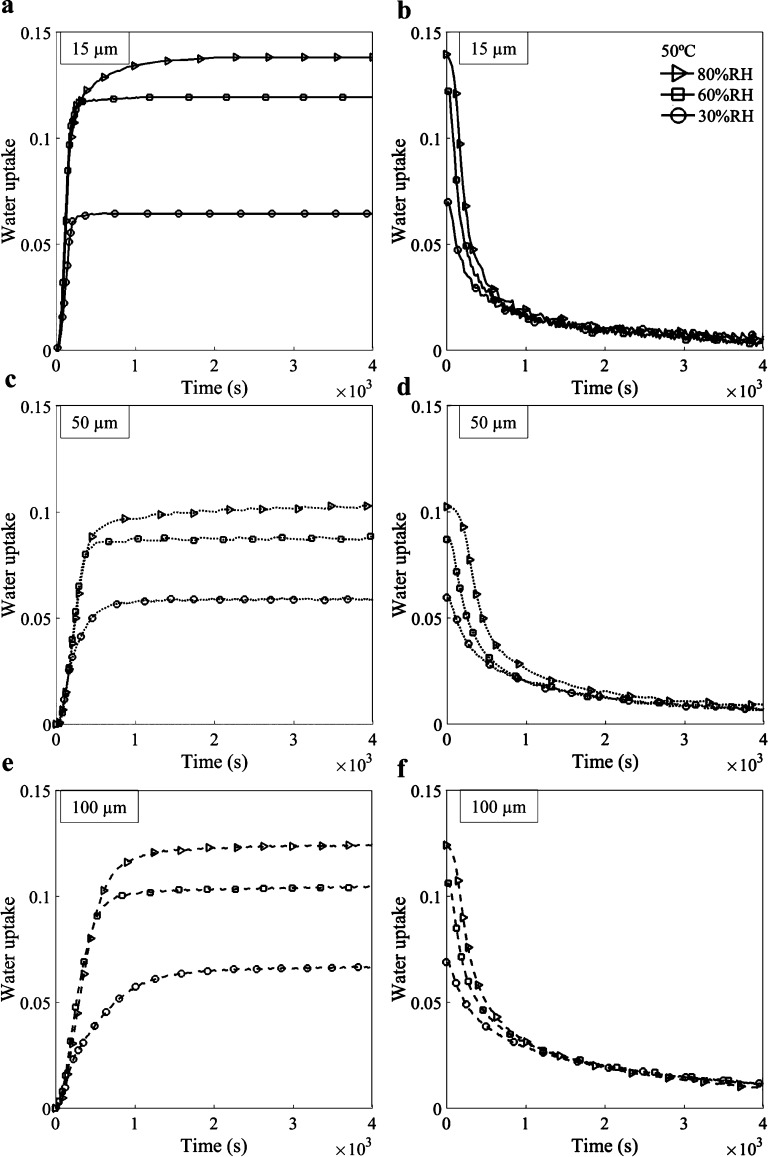
Figure 1 shows the evolution of the relative water uptake of pure PEDOT:PSS as a function of % RH change, at a constant temperature of 50 °C, for three thicknesses: (a,b) 15, (c,d) 50, and (e,f) 100 μm. The corresponding data for other temperatures are available in the Supporting Information (Figures S4–S7). Gravimetric experiments were found reproducible for all configurations. One test for each case is presented. Stabilization of mass was reached for all experimental configurations during the 3 h absorption test. We only plot the first hour of water absorption and the first hour of water desorption. The amount of absorbed water varies from a minimum of 3% (30% RH, 80 °C, see Figure S7) to a maximum of 56% (80% RH, 26 °C). All sorption curves (Figure 1a,c,d) display a saturation plateau that is constant until desorption starts.

Figure 1.

Figure 1

Open in a new tab

Sorption–desorption curves for (a,b) 15, (c,d) 50, and (e,f) 100 μm thick pure PEDOT:PSS films exposed to 30% RH, 60% RH, and 80% RH at 50 °C. The water uptake is dimensionless and defined by eq 1.

It is important to note the asymmetry between the absorption and desorption processes. During the absorption process, the polymer film uptakes water molecules relatively fast at the beginning, but the desorption process appears much slower. After a 1 h desorption process, we found that the PEDOT:PSS films still contained some residual mass uptake. We also observed that higher humidity level slightly increases the amount of residual water in the network.

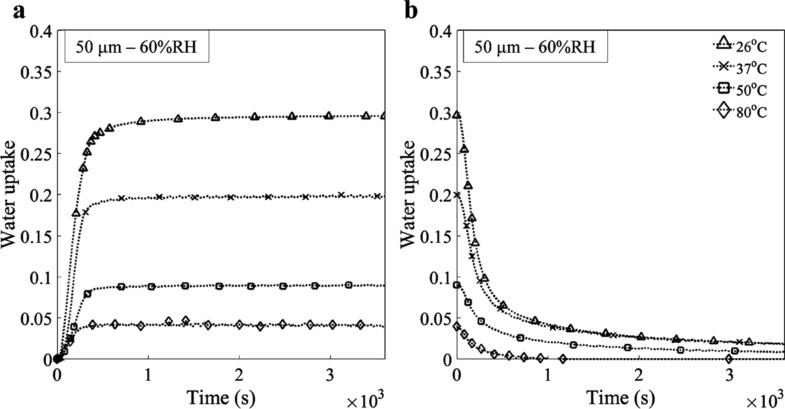
Figure 2 illustrates the sorption–desorption curves for a 50 μm pure PEDOT:PSS film exposed to 60% RH at four different temperatures. The amount of diffused water decreases with an increase in temperature. This result is consistent with Okuzaki’s findings.11 The saturation point is reached faster at higher temperatures, both for sorption (Figure 2a) and desorption (Figure 2b).

Figure 2.

Figure 2

Open in a new tab

(a) Sorption and (b) desorption curves for a 50 μm pure PEDOT:PSS film exposed to 60% RH at 26, 37, 50 ,and 80 °C.

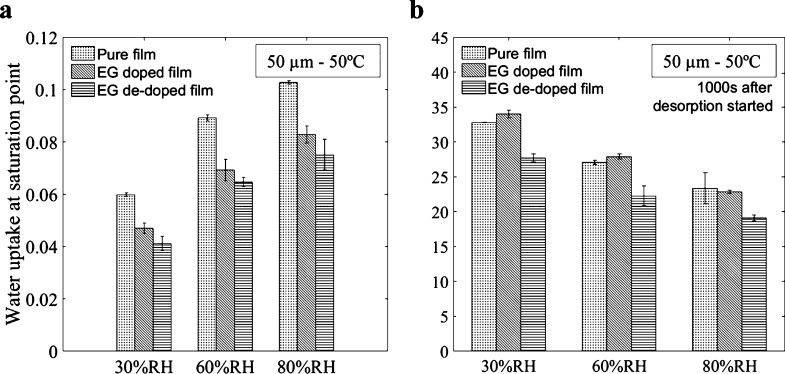
Figure 3a presents how the solvent treatment affects the water uptake process. We still do not introduce any model here and only focus on facts that can be directly observed from the experimental curves. The results indicate that the EG treatment (both pretreatment and post-treatment) induces a decrease of water uptake in the film, at saturation, in comparison with pure films, because of the structural changes it causes. The water uptake of the pretreated film is also always higher than the one of the post-treated film. This is consistent with the removal of PSS sites from the surface of the PEDOT:PSS film during the post-treatment process, which results in a decrease in the amount of reactive sites that bond with water molecules. In addition, the normalized water content of the post-treated film after 1000 s of desorption is less than that of pure and pretreated films (Figure 3b). A slightly faster water release is due to the lower number of reactions taking place in the polymer network associated with less PSS. It means that the part of free volume-associated water is more important in post-treated films than in other films, which is also consistent with the removal of PSS by washing. We would ascribe the slower desorption in the pretreated film compared to pure films to a reorganization of the microstructure (at constant PSS content). Because of the changes in conformation in the chains, the microstructure rearranges, resulting in a more dense network, less free volume, and slower desorption. This effect is, however, of second order as the associated variations are very small.

Figure 3.

Figure 3

Open in a new tab

(a) Water uptake of a 50 μm thick pure, pretreated, and post-treated PEDOT:PSS film exposed to 30% RH, 60% RH, and 80% RH at a saturation point. (b) Percent of water content after 1000 s of desorption started at 50 °C.

Discussion

These experimental results (asymmetry in kinetics between absorption and desorption and the existence of a non-negligible amount of residual water uptake after drying) suggest a non-Fickian absorption behavior. Indeed, we tried to represent these experimental results using a simple Fickian approach, but we could not represent both absorption and desorption with a unique set of material parameters. An example is provided in the Supporting Information (Section 1). Our results suggest a much more complex response that should be taken into account for the interactions between the diffused water and the substrate. The change in the microstructure triggered by the EG treatment can also strongly influence this interaction.

We adapt a more general model introduced by El Yagoubi and Lubineau.19 In addition to the classical diffusion, it takes into account the reaction of water molecules with the substrate that result in a global diffusion–reaction mechanism. The diffusing molecules, w, and the reactive site of the polymer, R, form a complex Y

graphic file with name ao9b02866_m004.jpg 4

where w, R, and Y coexist in the domain Ω. The unit of concentration is mol m–3.

We assume a first-order reaction for which the global rate of creation/consumption of water (rw) is given by the concentrations of reactants and products and by the rate constants (kh: rate constant of the forward reaction, kr: rate constant of the backward reaction) in a constant volume

graphic file with name ao9b02866_m005.jpg 5

where kh in m3 mol–1 s–1 and kr in s–1 are the functions of temperature.

The change of water concentration, at any point and any time, is the result of both the diffusion of free water and its interaction with the substrate (to create the complex Y made of the substrate and bonded water), such that

graphic file with name ao9b02866_m006.jpg 6

where j is the free-water flux. The full model is described in the Supporting Information (Section 2). The free-water flux (and diffusion of water in general) mainly depends on two material parameters: the diffusivity D (in m2 s–1) and the solubility S (in mol m–3 Pa–1). In case of non-Fickian diffusion, these material parameters eventually largely depend on the microstructure that evolves in time because of the reaction. Indeed, any structural reorganization will modify the free volume and the internal diffusion path, eventually modifying the effective macroscopic diffusion coefficient and solubility that measure how fast the diffusion is and how much can be absorbed, respectively. We model the effects of these microstructural changes in a simple way. From a macroscopic perspective, we assume a linear relationship among the reaction product Y, the diffusivity D, and/or the solubility S

graphic file with name ao9b02866_m007.jpg 7

As Y is the product of the reaction, with an initial concentration equal to zero, a linear relationship is the most simple model we can have that comes naturally from an asymptotic expansion around zero. Of course, more complex relations could be imagined, but these would not be relevant here as we could not discriminate between them based on the available experimental data. To summarize, this model describes the progressive conversion of the reactive sites (R) of the substrate into bonded water (Y) by interaction with the diffusing water (w). The initial concentration of the reactive site available in the polymer film to undergo chemical reaction is noted R0. The complete formulation of the model, for our case, and the numerical implementation in COMSOL Multiphysics and MATLAB Optimization toolbox, are given in the Supporting Information.

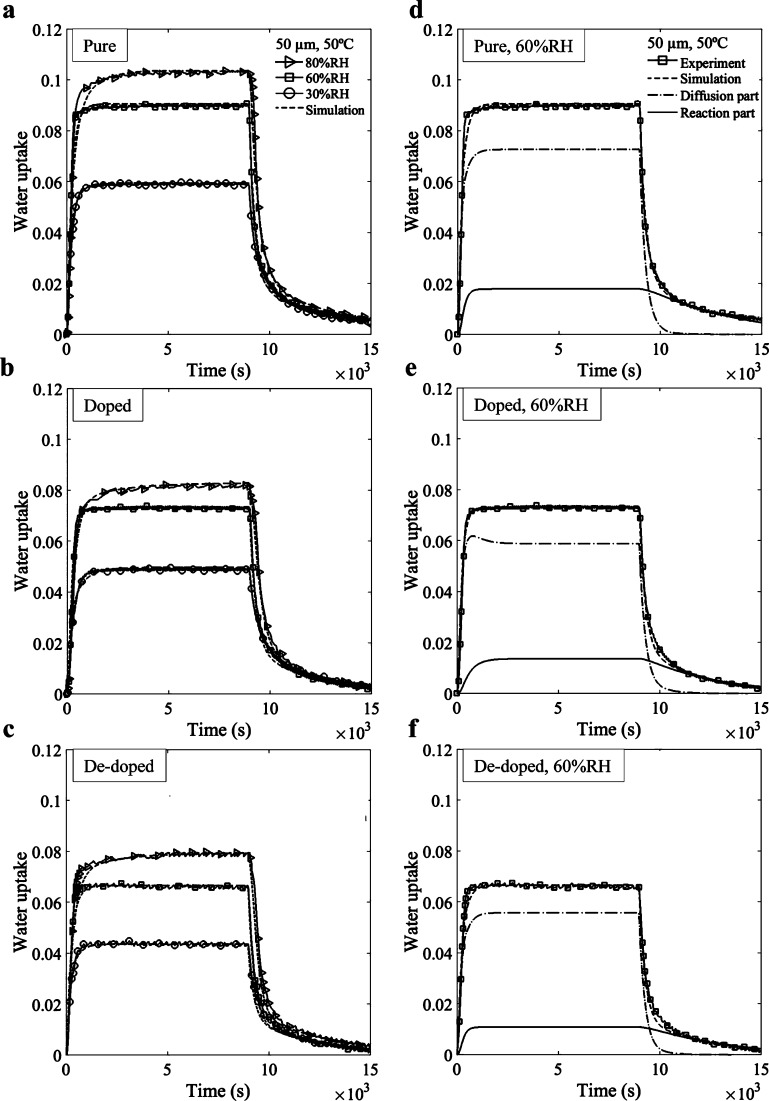
After a necessary calibration step (described in the Supporting Information), we first demonstrated that this diffusion–reaction model was able to describe the absorption–desorption results for pure, pretreated, and post-treated films at all (T, % RH) configurations. The data for the 50 μm film exposed to three humidity levels at 50 °C are presented in Figure 4a–c, where dashed lines represent the corresponding simulation results. Figure 4d–f shows the contribution of “diffusing” (w) and “reacting” (Y) water into the water uptake of pure, pretreated, and post-treated PEDOT:PSS films at 50 °C exposed to 60% RH. According to these results, mass uptake comes mainly from the diffusion of free water, but the bonded water described in the “reaction part” largely contributes to explain the response during desorption. The proposed model described all configurations with similar accuracies.

Figure 4.

Figure 4

Open in a new tab

(a–c) Comparison between the simulation and experimental curves for 50 μm at 50 °C; (d–f) contribution of “diffusing” and “reacting” water into the water uptake of PEDOT:PSS exposed to 60% RH.

It is then interesting to study and explain how the parameters of the model vary with the different configurations. The initial solubility constant S0, the initial diffusivity constant D0, and the quantity R0 of the sulfonate groups accessible for reaction at the beginning of the process are of particular interest. At room temperature, and for pure PEDOT:PSS, their values were S0 = 11.1 mol m–3 Pa–1, D0 = 1.6 × 10–12 m2 s–1, and R0 = 2730 mol m–3, respectively.

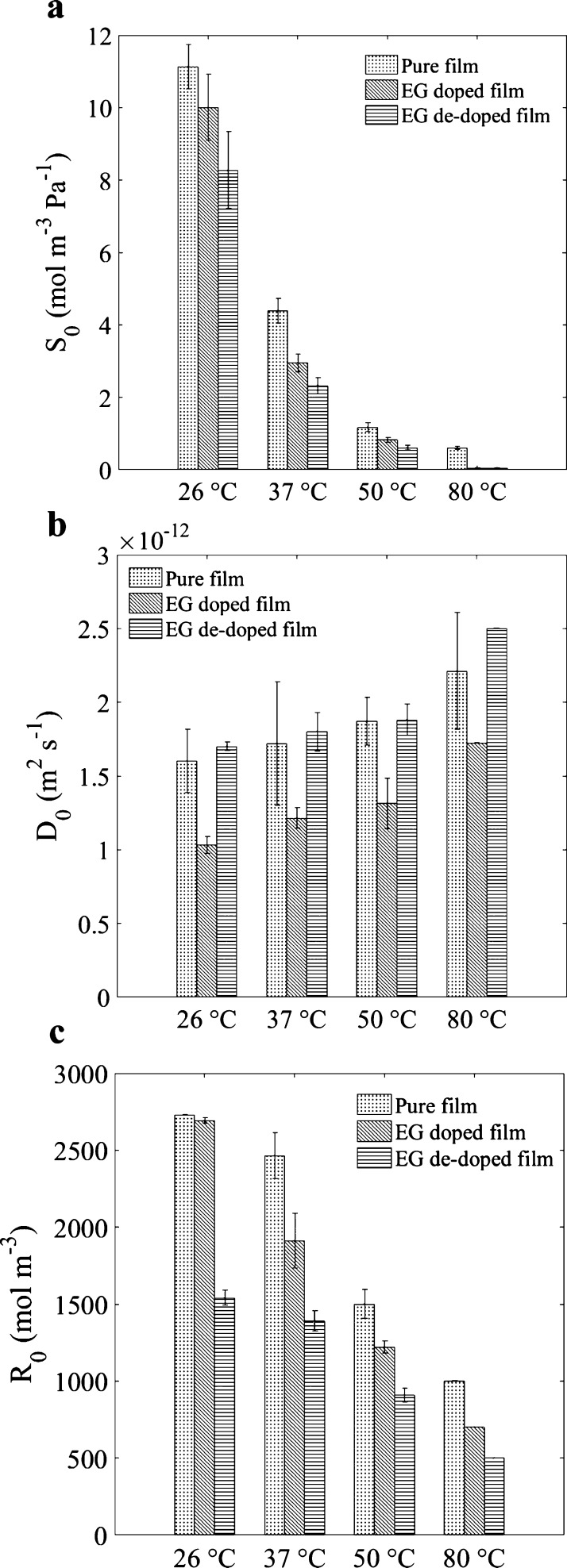
Figure 5 illustrates how the aforementioned parameters vary with various solvent treatments and at different temperatures. The way these parameters change, depending on the configuration, provides additional insights into the physical process and the following important parameters as discussed below.

Figure 5.

Figure 5

Open in a new tab

Evolution of (a) solubility constant S0, (b) diffusion constant D0, and (c) concentration of available reactive sites R0 with temperature increase for pure, EG-treated, and post-treated films.

About the Solubility Constant S0 with Temperature

In all cases, S0 decreases with a temperature increase (Figure 5a). Higher temperatures lead to the strengthening of the hydrogen bond between the PSS chain and the PEDOT:PSS grains.20 This means that it will be more difficult for the water molecules to bond with the sulfonate groups, as less space is made available for the uptake of water.

About the Diffusivity Constant D0 with Temperature

D0 increases with a temperature increase for all film types (Figure 5b); however, the change is not drastic, compared to S0. This can be explained by two competing mechanisms: (i) the increase in temperature causes an increase in the kinetic energy of diffusing molecules, resulting in an acceleration of the diffusion process (this mechanism usually explains the exponential change with temperature of the diffusivity constant for a pure Fickian process) and (ii) the drying polymer film becomes densely packed, decelerating the diffusion process. The first phenomenon is dominant, as D0 still has a positive trend with the increase in temperature.

About the Quantity of Available Sites for Reaction R0 with Temperature

The decrease of the reactive substrate concentration (R0) with temperature is also ascribed to the change in the microstructure. Less PSS is accessible to undergo a chemical reaction in the compacted structure, which translates into a reduction of the apparent quantities of sites available for reaction (R0). An in-depth investigation of the change in the microstructure with temperature can be found in ref (20)

The observed evolution of these parameters with the addition of solvents (Figure 5) is also compatible with the expected changes in the PEDOT:PSS film’s structural order as discussed below.

About the Evolution with EG Pretreatment

Adding an EG solvent into the PEDOT:PSS aqueous solution changes the conformation of the PEDOT chains from a benzoid (coiled) to a quinoid structure (linear).21 This leads to an increase in the number of interchain interactions because interactions among chains of linear conformation are facilitated, compared to the coiled conformation. Therefore, EG enhances the organization of the microstructure and promotes a more packed configuration.22,23 Such a microstructure will be more difficult to penetrate and will leave less free volume for the diffusion process to happen. These changes can be seen in Figure 5a, where the solubility of the pretreated film is lower than the solubility of the pure film; it results in the slow diffusion process (D0 decreased, see Figure 5b) and in the reduction of concentration of accessible sulfonate groups for bonding (see Figure 5c).

About the Evolution with EG Post-Treatment

The pure PEDOT:PSS film was post-treated by immersion into the EG solvent, which partially removes the hygroscopic PSS from the surface. Therefore, it uptakes the least amount of water among the three films (Figure 5a), resulting in a reduction in the concentration of reactive sites for water molecules to bond with (Figure 5c). The bulk of post-treated film remains similar to that of the pure film, which explains the similarity in the diffusion coefficients for both films (Figure 5b).

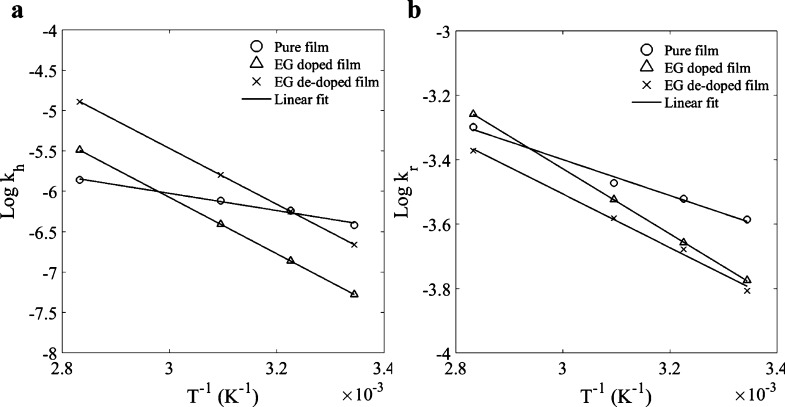
Finally, the chemical reaction between the diffusing molecules and the substrate is described in our model by the forward (kh) and backward (kr) rate constants, which follows Arrhenius’ law

graphic file with name ao9b02866_m008.jpg 8

where A is a pre-exponential factor, Rg is the universal gas constant, and Ea is the activation energy.

Figure 6 illustrates how the logarithm of rate constants changes with the inverse of temperature. The lines fit to Arrhenius’ law for the temperatures 26, 37, 50, and 80 °C. The EG treatment significantly affects the temperature dependence of the rate constants. The differences between the slopes for pure and treated films can be attributed to the morphological reorganization taking place after the solvent treatment. The values of Ea for the different film types are given in Table 1. For both rate constants, the activation energies of EG-treated films are higher than those for the pure film.

Figure 6.

Figure 6

Open in a new tab

Change of rate constants (a) kh and (b) kr with temperature, for pure, EG-treated, and post-treated films.

Table 1. Activation Energy Values for kh and kr.

Ea for pure pretreated post-treated
forward 20 948 67 093 66 384
backward 12 057 19 399 15 302
Open in a new tab

Conclusions

We have studied the absorption–desorption mechanism of PEDOT:PSS and investigated the effects of EG treatment (pretreatment and post-treatment). Gravimetric tests were used to provide the evolution of water uptake in polymer films at different temperatures and RH levels. Following the pretreatment with EG, a morphological reorganization of the polymer network and a loss in free volume resulted in a decrease in water uptake. For the post-treated film, the removal of the hydrophilic sites of PSS contributed to the reduction in the amount of water reacting with the polymer.

The water transport process was described using a diffusion–reaction model by implementing it in a COMSOL Multiphysics and MATLAB optimization toolbox. A set of parameters was identified to describe the kinetics of sorption and desorption. The simulation results showed the same trend as the one found in experimental tests for solubility change. The evolution of each key parameter with respect to temperature and solvent treatment was found consistent with the physical considerations.

This study highlights the dependence of the behavior of PEDOT:PSS on the environmental conditions and the influence of EG treatment on water transport kinetics. This is the first step in the establishment of a complete Multiphysics model needed for the design of complex PEDOT:PSS-based components.

Acknowledgments

The research reported in this publication was supported by the funding from King Abdullah University of Science and Technology (KAUST), under award number BAS/1/1315-01-01.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b02866.

  • Study about the validity of the Fickian diffusion model, description of the diffusion–reaction model, and database with all experimental results (PDF)

Author Contributions

G.L. conceived the study. L.Z. and V.F. conducted the experiments and simulation. All authors analyzed the results and wrote the manuscript.

The authors declare no competing financial interest.

Notes

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Supplementary Material

ao9b02866_si_001.pdf (2.5MB, pdf)

References

  1. Cicoira F.; Santato C.. Organic Electronics: Emerging Concepts and Technologies, 3rd ed.; John Wiley & Sons, 2013. [Google Scholar]
  2. Kim N.; Kee S.; Lee S. H.; Lee B. H.; Kahng Y. H.; Jo Y.-R.; Kim B.-J.; Lee K. Highly conductive PEDOT:PSS nanofibrils induced by solution-processed crystallization. Adv. Mater. 2014, 26, 2268–2272. 10.1002/adma.201304611. [DOI] [PubMed] [Google Scholar]
  3. Wu F.; Li P.; Sun K.; Zhou Y.; Chen W.; Fu J.; Li M.; Lu S.; Wei D.; Tang X.; Zang Z.; Sun L.; Liu X.; Ouyang J. Conductivity Enhancement of PEDOT:PSS via Addition of Chloroplatinic Acid and Its Mechanism. Adv. Electron. Mater. 2017, 3, 1700047. 10.1002/aelm.201700047. [DOI] [Google Scholar]
  4. Wang C.; Sun K.; Fu J.; Chen R.; Li M.; Zang Z.; Liu X.; Li B.; Gong H.; Ouyang J. Enhancement of Conductivity and Thermoelectric Property of PEDOT:PSS via Acid Doping and Single Post-Treatment for Flexible Power Generator. Adv. Sustainable Syst. 2018, 2, 1800085. 10.1002/adsu.201800085. [DOI] [Google Scholar]
  5. Okuzaki H.Soft Actuators: Materials, Modeling, Applications, and Future Perspectives; Asaka K., Okuzaki H., Eds.; Springer, 2014; Chapter 8, pp 111–126. [Google Scholar]
  6. Zhang S.; Cicoira F. Water-Enabled Healing of Conducting Polymer Films. Adv. Mater. 2017, 29, 1–6. 10.1002/adma.201770291. [DOI] [PubMed] [Google Scholar]
  7. Lin P.; Yan F.; Yu J.; Chan H. L. W.; Yang M. The application of organic electrochemical transistors in cell-based biosensors. Adv. Mater. 2010, 22, 3655–3660. 10.1002/adma.201000971. [DOI] [PubMed] [Google Scholar]
  8. Nilsson D.; Kugler T.; Svensson P. O.; Berggren M. An all-organic sensor-transistor based on a novel electrochemical transducer concept printed electrochemical sensors on paper. Sens. Actuators, B 2002, 86, 193–197. 10.1016/s0925-4005(02)00170-3. [DOI] [Google Scholar]
  9. Hu L.; Li M.; Yang K.; Xiong Z.; Yang B.; Wang M.; Tang X.; Zang Z.; Liu X.; Li B.; Xiao Z.; Lu S.; Gong H.; Ouyang J.; Sun K. PEDOT:PSS monolayers to enhance the hole extraction and stability of perovskite solar cells. J. Mater. Chem. A 2018, 6, 16583–16589. 10.1039/c8ta05234d. [DOI] [Google Scholar]
  10. Chen R.; Sun K.; Zhang Q.; Zhou Y.; Li M.; Sun Y.; Wu Z.; Wu Y.; Li X.; Xi J.; Ma C.; Zhang Y.; Ouyang J. Sequential Solution Polymerization of Poly(3,4-ethylenedioxythiophene) Using V2O5 as Oxidant for Flexible Touch Sensors. iScience 2019, 12, 66–75. 10.1016/j.isci.2019.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Okuzaki H.; Suzuki H.; Ito T. Electrically driven PEDOT/PSS actuators. Synth. Met. 2009, 159, 2233–2236. 10.1016/j.synthmet.2009.07.054. [DOI] [Google Scholar]
  12. Okuzaki H.; Hosaka K.; Suzuki H.; Ito T. Effect of temperature on humido-sensitive conducting polymer actuators. Sens. Actuators, A 2010, 157, 96–99. 10.1016/j.sna.2009.10.022. [DOI] [Google Scholar]
  13. Okuzaki H.; Kuwabara T.; Kunugi T. Theoretical study of sorption-induced bending of polypyrrole films. J. Polym. Sci., Part B: Polym. Phys. 1998, 36, 2237–2246. . [DOI] [Google Scholar]
  14. Okuzaki H.; Kuwabara T.; Kondo T. Role and effect of dopant ion on sorption-induced motion of polypyrrole films. J. Polym. Sci., Part B: Polym. Phys. 1998, 36, 2635–2642. . [DOI] [Google Scholar]
  15. Okuzaki H.; Kondo T.; Kunugi T. Characteristics of water in polypyrrole films. Polymer 1999, 40, 995–1000. 10.1016/s0032-3861(98)00319-x. [DOI] [Google Scholar]
  16. Lang U.; Naujoks N.; Dual J. Mechanical characterization of PEDOT:PSS thin films. Synth. Met. 2009, 159, 473–479. 10.1016/j.synthmet.2008.11.005. [DOI] [Google Scholar]
  17. Kuş M.; Okur S. Electrical characterization of PEDOT:PSS beyond humidity saturation. Sens. Actuators, B 2009, 143, 177–181. 10.1016/j.snb.2009.08.055. [DOI] [Google Scholar]
  18. Sarkar B.; Jaiswal M.; Satapathy D. K. Swelling kinetics and electrical charge transport in PEDOT:PSS thin films exposed to water vapor. J. Phys.: Condens. Matter. 2018, 30, 225101. 10.1088/1361-648X/aabe51. [DOI] [PubMed] [Google Scholar]
  19. El Yagoubi J.; Lubineau G.; Roger F.; Verdu J. A fully coupled diffusion-reaction scheme for moisture sorption-desorption in an anhydride-cured epoxy resin. Polymer 2012, 53, 5582–5595. 10.1016/j.polymer.2012.09.037. [DOI] [Google Scholar]
  20. Zhou J.; Anjum D. H.; Chen L.; Xu X.; Ventura I. A.; Jiang L.; Lubineau G. The temperature-dependent microstructure of PEDOT/PSS films: insights from morphological, mechanical and electrical analyses. J. Mater. Chem. C 2014, 2, 9903–9910. 10.1039/c4tc01593b. [DOI] [Google Scholar]
  21. Ouyang J.; Xu Q.; Chu C. W.; Yang Y.; Li G.; Shinar J. On the mechanism of conductivity enhancement in poly(3,4- ethylenedioxythiophene):poly(styrene sulfonate) film through solvent treatment. Polymer 2004, 45, 8443–8450. 10.1016/j.polymer.2004.10.001. [DOI] [Google Scholar]
  22. Wei Q.; Mukaida M.; Naitoh Y.; Ishida T. Morphological change and mobility enhancement in PEDOT:PSS by adding co-solvents. Adv. Mater. 2013, 25, 2831–2836. 10.1002/adma.201205158. [DOI] [PubMed] [Google Scholar]
  23. Xia Y.; Ouyang J. Significant Conductivity Enhancement of Conductive Poly(3,4-ethylenedioxythiophene):Poly(styrenesulfonate) Films through a Treatment with Organic Carboxylic Acids and Inorganic Acids. ACS Appl. Mater. Interfaces 2010, 2, 474–483. 10.1021/am900708x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b02866_si_001.pdf (2.5MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES