Temperature-independent thermal radiation

Significance

Conventional wisdom states that the hotter an object is, the brighter it glows. This is the case for thermal light at any wavelength and enables applications such as infrared imaging and noncontact thermometry. We demonstrate a coating that emits the same amount of thermal radiation irrespective of temperature, within a temperature range of about 30 °C. This is accomplished using samarium nickel oxide—a quantum material that changes strongly but gradually as a function of temperature. This is the first time that temperature-independent thermal radiation has been demonstrated, and has substantial implications for infrared camouflage, privacy shielding, and radiative heat transfer.

Abstract

Thermal emission is the process by which all objects at nonzero temperatures emit light and is well described by the Planck, Kirchhoff, and Stefan–Boltzmann laws. For most solids, the thermally emitted power increases monotonically with temperature in a one-to-one relationship that enables applications such as infrared imaging and noncontact thermometry. Here, we demonstrated ultrathin thermal emitters that violate this one-to-one relationship via the use of samarium nickel oxide (SmNiO₃), a strongly correlated quantum material that undergoes a fully reversible, temperature-driven solid-state phase transition. The smooth and hysteresis-free nature of this unique insulator-to-metal phase transition enabled us to engineer the temperature dependence of emissivity to precisely cancel out the intrinsic blackbody profile described by the Stefan–Boltzmann law, for both heating and cooling. Our design results in temperature-independent thermally emitted power within the long-wave atmospheric transparency window (wavelengths of 8 to 14 µm), across a broad temperature range of ∼30 °C, centered around ∼120 °C. The ability to decouple temperature and thermal emission opens a gateway for controlling the visibility of objects to infrared cameras and, more broadly, opportunities for quantum materials in controlling heat transfer.

The total amount of power thermally emitted by a surface in free space can be obtained by integrating its spectral radiance—given by Planck’s law and an emissivity—over all wavelengths and hemispherical angles (1, 2). Assuming negligible angular dependence of the emissivity and wrapping the angular integral into the blackbody distribution, $I_{BB}\left(\lambda ,T\right)$, this relationship can be expressed as

$$A{\displaystyle \underset{\lambda }{\int }d\lambda \hspace{0.17em}\epsilon \left(\lambda ,T\right)I_{BB}\left(\lambda ,T\right)}=A{\epsilon }_{tot}\left(T\right)\sigma T^4,$$ [1]

where $A$ is the surface area, $\epsilon \left(\lambda ,T\right)$ is the spectral emissivity, $\lambda$ is the free-space wavelength, $T$ is the temperature, and $\sigma$ is the Stefan–Boltzmann constant. The total emissivity, ${\epsilon }_{tot}\left(T\right)$, can have a gradual temperature dependence even if the spectral emissivity has no such dependence due to the integration of $\epsilon \left(\lambda \right)I_{BB}\left(\lambda ,T\right)$ (3); nevertheless, this dependence is usually dwarfed by the $T^4$ term, and so ${\epsilon }_{tot}$ can often be considered to be approximately constant. Thus, the Stefan–Boltzmann law yields a one-to-one mapping between the temperature of an object and the emitted power, resulting in the conventional wisdom that hotter objects emit more light (Fig. 1 A and C) and enabling applications such as infrared imaging and noncontact thermometry (4, 5).

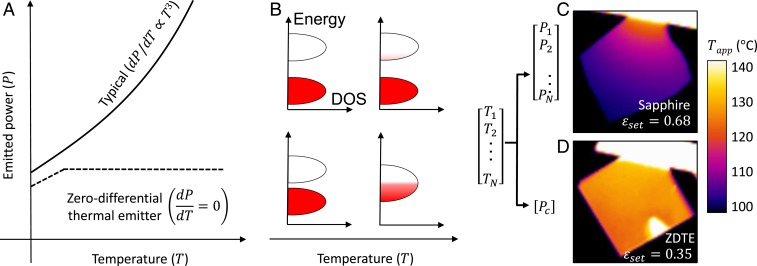
Fig. 1.

Comparison between a typical thermal emitter and a zero-differential thermal emitter (ZDTE). (A and B) For a typical emitter, for example comprising a semiconductor or insulator (cartoon band diagram in B, Top), any change in emission from a temperature-dependent change in materials properties is dwarfed by the $T^4$ dependence in the Stefan–Boltzmann law. Conversely, a ZDTE decouples temperature and thermal radiation over some temperature range and thus can only be made using a material with a very strong temperature dependence. In our implementation, we use the hysteresis-free insulator-to-metal phase transition in samarium nickelate (SmNiO₃) to achieve this behavior (B, Bottom). DOS, density of states. (C and D) LWIR images of samples mounted to hang off the edge of a heater stage, such that a temperature gradient is established from hot to cold. (C) A reference sample with a constant emissivity—in this case, a sapphire wafer—and (D) a ZDTE based on SmNiO₃. The color bar encodes the apparent temperature, obtained by assuming a particular set emissivity, ${\epsilon }_{set}$, which was chosen such that the sample region just below the heat stage appeared to be at 130 °C, which is the actual temperature at that point (see more discussion in Methods). For sapphire, there is a one-to-one relationship between temperature and thermally emitted power. Conversely, the ZDTE exhibits a constant emitted power over a range of temperatures, here ∼100 to 135 °C.

This assumption of a near-constant emissivity must be reexamined for thermal emitters comprising materials whose optical properties can be widely tunable with temperature (i.e., thermochromics). For example, an emissivity that increases with temperature can result in emitted power growing faster than $T^4$ (6, 7), and an emissivity that rapidly decreases with temperature can overwhelm and reverse the slope of the typical Stefan–Boltzmann curve (8, 9).

Here, we show that it is possible to achieve a complete breakdown of the conventional one-to-one mapping between the temperature and the thermally emitted power, $P$. A thermal-emission coating with this unique property can serve as a radiator that outputs a fixed amount of heat irrespective of its temperature and can conceal differences in temperature across an object from infrared imagers. This condition can be written as $\partial P/\partial T=0$ and occurs when ${\epsilon }_{tot}=\gamma T^{-4}$, where $\gamma$ is a constant with units of kelvin (4). A surface with ${\epsilon }_{tot}$ that fits this form over some temperature range is henceforth referred to as a zero-differential thermal emitter (ZDTE). Achieving ZDTE behavior using real materials is extremely challenging: The necessary rate of change of the emissivity with temperature is much larger than what can be attained using conventional materials (e.g., with band semiconductors such as silicon, via the temperature-dependent population of electrons in the conduction band; Fig. 1B) but is smaller than that of materials with abrupt phase transitions (e.g., vanadium dioxide; refs. 8 and 10). Furthermore, this condition is only possible for a hysteresis-free temperature dependence of the emissivity; otherwise, the ZDTE condition may only be satisfied during either heating or cooling, but not both (further discussed in SI Appendix, section 1).

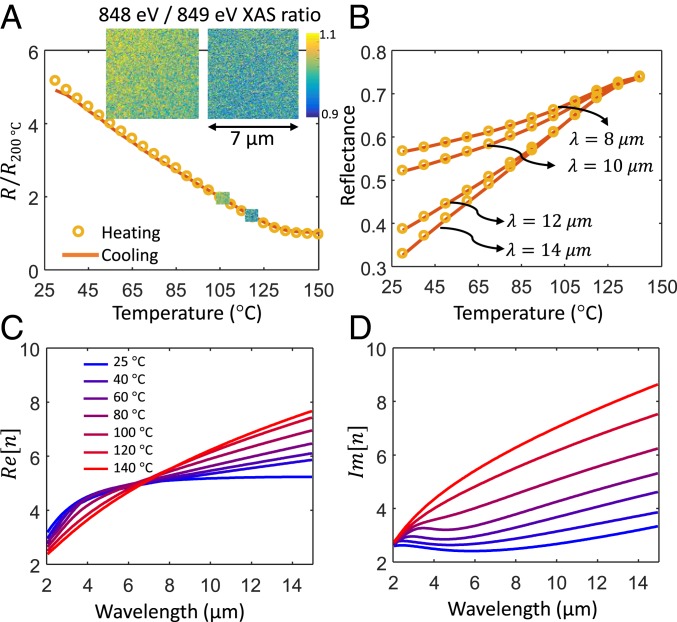
Here, we demonstrate ZDTE in the 8- to 14-µm atmospheric transparency window (11) using samarium nickel oxide (SmNiO₃), a correlated perovskite that features strong yet relatively gradual evolution of its optical properties over the temperature range of ∼40 to ∼140 °C, resulting from a fully reversible and hysteresis-free thermally driven insulator-to-metal transition (IMT) (12–16). The thermal IMT in SmNiO₃ is due to charge disproportionation in the Ni site and involves subtle changes in the Ni–O–Ni bond angle (12, 16). In our SmNiO₃ films (Methods), this thermally driven transition is reversible over many cycles and has essentially no hysteresis in both electrical (Fig. 2A) and optical measurements (Fig. 2B), in stark contrast to many other materials with strong IMTs [e.g., vanadium dioxide (17)]. Hysteresis-free IMTs can be found in rare-earth nickelates with high phase-transition temperatures, where negligible or complete absence of hysteresis may be due to the decoupling of the IMT with antiferromagnetic ordering and faster phase-transformation kinetics at higher temperatures (18, 19). The unique nature of this IMT is also directly observed in our spatially resolved X-ray absorption spectroscopy (XAS) maps across the thermal transition [Fig. 2 A, Inset], which demonstrate smooth variation with temperature (i.e., the absence of any metallic/insulating domain texture at any temperature) down to a ∼20-nm length scale, including for temperatures deep within the IMT; see Methods and SI Appendix, section 5 for details. No spatial features other than detector noise were observed. The trend in these spatial maps (including additional data in SI Appendix, section 5) suggests a smooth cross-over from the insulating limit to the metallic one, which is accompanied by a homogeneous phase landscape. The SI Appendix includes experimental data showing stability over many cycles (SI Appendix, section 2) and X-ray diffraction measurements that further help explain the transition behavior (SI Appendix, section 3).

Fig. 2.

Hysteresis-free insulator-to-metal phase transition in SmNiO₃. (A) Normalized temperature-dependent electrical resistance of our SmNiO₃ thin film grown on a sapphire substrate and (B) mid-infrared reflectance at several representative wavelengths, during both heating and cooling, showing the hysteresis-free nature of the IMT in SmNiO₃. The insets in A are nanoscale XAS maps at 105 and 120 °C, where the ratio of X-ray absorption at 848 eV to that at 849 eV is plotted as an indication of the metallic/insulating properties; no features other than detector noise are observed, indicating a gradual transition with no observable domain texture. (C and D) Temperature-dependent (C) real and (D) imaginary parts of the complex refractive index of the SmNiO₃ film, as a function of wavelength across the mid infrared, extracted using spectroscopic ellipsometry.

To enable design of thermal emitters using SmNiO₃, we performed temperature-dependent variable-angle spectroscopic ellipsometry over the 2- to 16-µm wavelength range, through the entire range of the phase transition (Fig. 2 C and D). The resulting complex refractive-index data are consistent with the film becoming gradually more metallic from room temperature to ∼140 °C. We note that while gradual transitions are generally considered to be less useful than abrupt transitions for electronic and optical switching technologies, here the gradual and hysteresis-free nature of the IMT in SmNiO₃ is essential for the realization of ZDTEs.

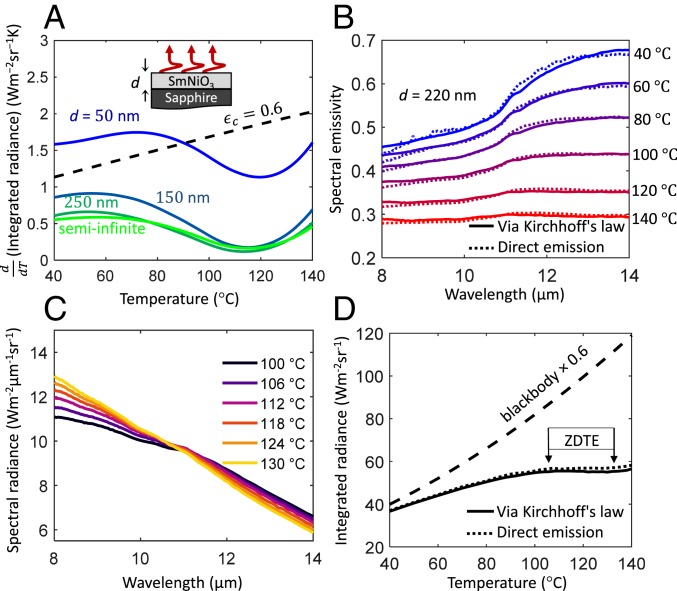
To minimize fabrication complexity and cost and thus realize robust and large-area ZDTEs, we explored designs based on unpatterned thin films of SmNiO₃. We used the temperature-dependent optical properties in Fig. 2 C and D and well-established optical thin-film calculations (20) to find the necessary combination of thickness of an SmNiO₃ film and a substrate that supports SmNiO₃ synthesis (Fig. 3A and SI Appendix, section 4) to achieve ZDTE over the 8- to 14-µm atmospheric transparency window. In Fig. 3A, we plotted the calculated temperature derivative of the emitted integrated radiance for several thicknesses of SmNiO₃ on sapphire, which indicates that ZDTE can be achieved for SmNiO₃ thickness of ∼150 nm or greater. The result does not change much for SmNiO₃ films thicker than ∼250 nm, indicating that the optical properties of the substrate do not affect the emissivity, making SmNiO₃ a versatile surface coating that can be utilized for scalable technologies.

Fig. 3.

Zero-differential thermal emission. (A) Calculated temperature derivative of the emitted radiance, integrated over the 8- to 14-µm atmospheric transparency window, of an SmNiO₃ film with thicknesses $d$ from 50 nm to infinity, on a semi-infinite sapphire substrate. (B) Measured wavelength- and temperature-dependent emissivity of our ZDTE, comprising a ∼220-nm film of SmNiO₃ on a sapphire substrate, via direct emission (dotted) and Kirchhoff’s law using reflectance measurements (solid). (C) The temperature-dependent spectral radiance of the ZDTE, which is the product of the spectral emissivity in B and the Planck distribution. (D) Thermally emitted radiance of our ZDTE, integrated over 8 to 14 µm, compared to that of a blackbody.

Our fabricated planar device consists of a ∼220-nm SmNiO₃ film grown on a c-plane sapphire substrate (Fig. 3 A, Inset; see Methods for details), from which we measured the emissivity and the resulting thermally emitted spectral radiance. Because the resulting structure is opaque in our wavelength region of interest [due to the optical losses in SmNiO₃ as well as in sapphire (21)] and flat on the scale of the wavelength, Kirchhoff’s law can be used to calculate the normal-direction emissivity ${\epsilon }_N\left(\lambda ,T\right)$ from normal-incidence reflectance measurements: ${\epsilon }_N\left(\lambda ,T\right)=1-R_N\left(\lambda ,T\right)$ (see Methods for details). We confirmed this result by measuring the thermal emission directly, normalizing to a laboratory blackbody consisting of a vertically oriented 0.1-mm-tall carbon nanotube forest (Methods). Care was taken to isolate the sample thermal emission from the thermal background radiated by the various components of our instrument (22) (SI Appendix, section 6). The results obtained from these two measurements are in excellent agreement (Fig. 3B).

We integrated the measured spectral radiance (Fig. 3C) over the 8- to 14-µm window to obtain the total thermally emitted integrated radiance as a function of temperature, which showed the desired ZDTE effect within a ∼30 °C temperature window centered around ∼120 °C (Fig. 3D). Away from the center of the phase transition of SmNiO₃, that is, below ∼80 and above ∼140 °C, the radiance-vs.-temperature profile becomes monotonically increasing, as expected for a typical nonthermochromic thermal emitter. We note that the ZDTE effect is quite robust for different angles of emission (SI Appendix, section 7).

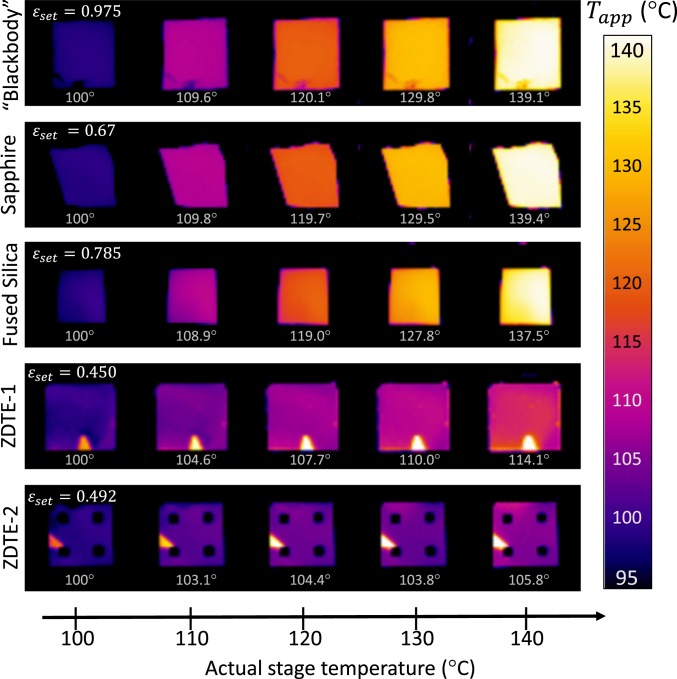
The presence of the zero-differential region has profound implications for infrared imaging and control of infrared visibility. To demonstrate this, we performed a model experiment where two samples—our ZDTE and a reference sapphire wafer—were mounted on a temperature-controlled chuck such that only a corner was touching the chuck and most of the sample was suspended in air, resulting in a temperature gradient from ∼140 °C directly on top of the chuck to ∼105 °C at the corner of the suspended area. When imaged with a long-wave infrared (LWIR) camera, the gradient is readily observable on the sapphire reference (Fig. 1B) but almost completely disappears on our SmNiO₃-based ZDTE (Fig. 1D). Note that the bright spot in the bottom side of the ZDTE sample corresponds to a region with no SmNiO₃ (i.e., it is simply sapphire). This is the area covered by the clip used to mount the sample in the sputtering chamber. The apparent temperature difference across the samples based on the camera image was ∼34 °C for the sapphire and ∼9 °C for the ZDTE. The same phenomenon is observed in Fig. 4, where we show the temperature evolution of the infrared appearance of SmNiO₃-based ZDTEs compared to our laboratory blackbody reference (carbon nanotube forest) and sapphire and fused-silica wafers. Note that we numerically analyzed the temperature drop across the thickness of the sapphire wafer (i.e., from the heat stage to the surface of the sample) and found that it is less than 0.1 °C (SI Appendix, section 8).

Fig. 4.

Long-wavelength infrared (LWIR) images of samples held at temperatures from 100 to 140 °C. The emissivities of the laboratory blackbody (carbon nanotube forest), sapphire wafer, and fused SiO₂ wafer do not change appreciably over this temperature range. The emissivities of our SmNiO₃-based ZDTEs change as a function of temperature, and thus effectively mask the temperature differences from the camera. The apparent temperature is plotted (like in Fig. 1 C and D) with ${\epsilon }_{set}$ for each sample selected such that for a stage temperature of 100 °C the infrared camera returned this value as the temperature reading. The dark squares on the bottom row are metal electrodes that were used for the resistance measurements in Fig. 2A.

We note that the presence of zero-differential emission does not necessarily guarantee completely temperature-independent infrared signatures. For example, slight differences can still be observed in the emission from our ZDTEs at 110 °C vs. 140 °C in Fig. 4, resulting from a combination of effects that include imperfect cancelation of the blackbody curve and the change of the reflected light from the environment, since a change in emissivity coincides with a change in reflectance. The latter can be compensated during the design of ZDTEs by considering both the emitted and reflected light, assuming a particular background temperature.

In conclusion, we demonstrated that the typical one-to-one relationship between temperature and thermal radiation can be severed using zero-differential thermal emitter (ZDTE) coatings based on SmNiO₃, a quantum material featuring a hysteresis-free thermally driven insulator-to-metal transition (IMT). The temperature range of the zero-differential emission effect can be widely tuned by strain, doping, or tilt control of SmNiO₃, which can shift the transition range to room temperature and even below (15, 23–25). For example, alloys of samarium and neodymium nickelates can have IMT temperatures roughly between −100 °C and 100 °C depending on the specific composition (26), which may enable ZDTE design over a wide range of temperatures (SI Appendix, section 9). The ability to decouple temperature and thermal radiation with our simple design enables approaches to conceal heat signatures over large areas, for example for wearable personal privacy technologies, and also has implications for thermal management in space. More broadly, this demonstration can motivate areas of inquiry for quantum materials that possess highly tunable electronic structures.

Methods

Materials Synthesis.

The SmNiO₃ films were grown using magnetron sputtering. The sputtering power was set to 90 W direct current for the Ni target and 170 W radio frequency for the Sm target. The total pressure during deposition was kept at 5 mTorr under a constant gas flow of 40 standard cubic centimeters per minute (sccm) for Ar and 10 sccm for O₂. The as-deposited films were subsequently transferred into a home-built high-pressure chamber and annealed in 1,400-pounds-per-square-inch oxygen gas at 500 °C for 24 h to form the perovskite phase. The electrical resistance of SmNiO₃ films (Fig. 2A) was measured on a temperature-controlled probe station by sweeping the voltage from −0.1 V to 0.1 V with a Keithley 2635A source meter, with Pt electrodes on top of the SmNiO₃ films. The electrodes can be seen in the bottom row of Fig. 4.

Nanoscale XAS.

The X-ray absorption spectroscopy (XAS)/X-ray photoemission electron microscopy (XPEEM) experiments were performed at the XPEEM end station of the Electron Spectro-Microscopy beamline (21-ID-2) at the National Synchrotron Light Source II. The sample was illuminated with a focused monochromatic soft X-ray beam with a photon energy tuned around the Ni-L₃ resonance (840 to 850 eV). The temperature was controlled to within 0.1 °C of the target set point. All images were drift-corrected and the same field of view was recovered at each temperature. All measurements were taken with linear-horizontal polarized light at an incident angle of 73° to the surface normal. The SmNiO₃ film used for XAS/XPEEM measurements was deposited epitaxially on an LaAlO₃ (001) substrate. The XAS/XPEEM is a spatially resolved probe to measure the Ni valence electronic states during the IMT. The metallic/insulating phases can be distinguished by different XAS spectral shapes. The maps in the Fig. 2 A, Inset are ratios of the absorption coefficients at 848 and 849 eV, which can be used as a proxy for spatial identification of the metallic/insulating phases. This ratio is 1.02 in the insulating phase of SmNiO₃ and 0.98 in the metallic phase (SI Appendix, section 5).

Optical Measurements.

The temperature-dependent complex refractive index of SmNiO₃ was measured using a Woollam IR VASE MARK II spectroscopic ellipsometer with a temperature-controlled stage, assuming the film thickness obtained from scanning electron microscope (SEM) imaging of the cross-section. The fitting was performed using WVASE software. The SmNiO₃ film was assumed to be isotropic, whereas anisotropy in the sapphire was included in the fitting model. The reflectance measurements were obtained with a Bruker Vertex 70 FTIR and a Hyperion 2000 microscope with a reflective objective (numerical aperture [N.A.] = 0.4), and a Linkam THMS600 temperature-controlled stage. The direct-emission measurements were obtained with the temperature stage and sample in the Fourier transform infrared (FTIR) spectrometer sample compartment, using a parabolic mirror for collection (N.A. = 0.05). In both direct-emission and Kirchhoff’s-law measurements, we used a liquid-nitrogen-cooled mercury–cadmium–telluride detector and a potassium bromide beam splitter. A gold mirror was used as the reflection reference, whereas a vertically aligned carbon nanotube forest on a silicon substrate was used as the emission reference (see SI Appendix, section 6 for details about reference calibration and the accounting for background thermal radiation). LWIR imaging was carried out using an FLIR A325sc camera, sensitive to the 7.5- to 13-μm range.

The color bars of the infrared images in Figs. 1 C and D and 4 report the apparent temperature, given some emissivity setting, ${\epsilon }_{set}$, in the FLIR camera software. The value of ${\epsilon }_{set}$ used for each image is provided directly on the image. In Fig. 1 C and D and Fig. 4, we selected ${\epsilon }_{set}$ such that the apparent temperature corresponded to the actual temperature at some particular point. In Fig. 1 C and D, this point is at the very top of the sample where it just touches the temperature stage; in Fig. 4, this is done for each sample at 100 °C.

Optics Calculations.

For the calculation of emissivity, we used the transfer-matrix method together with the optical properties from ellipsometry to obtain the absorptivity, which we converted to emissivity using Kirchhoff’s law. The emitted spectrum was then calculated by multiplying the spectral emissivity by the Planck distribution at the appropriate temperature, which could then be integrated over the midinfrared transparent window of 8 to 14 μm to obtain the emitted power.

Data Availability.

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.