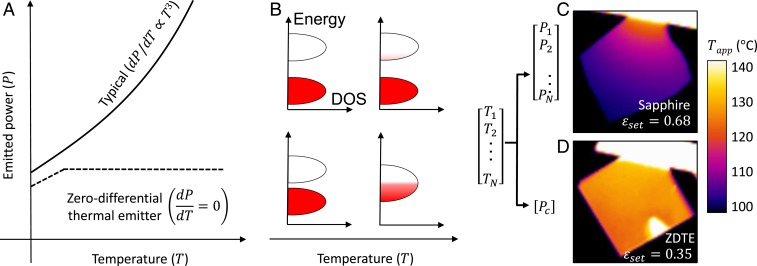
Fig. 1.

Comparison between a typical thermal emitter and a zero-differential thermal emitter (ZDTE). (A and B) For a typical emitter, for example comprising a semiconductor or insulator (cartoon band diagram in B, Top), any change in emission from a temperature-dependent change in materials properties is dwarfed by the $T^4$ dependence in the Stefan–Boltzmann law. Conversely, a ZDTE decouples temperature and thermal radiation over some temperature range and thus can only be made using a material with a very strong temperature dependence. In our implementation, we use the hysteresis-free insulator-to-metal phase transition in samarium nickelate (SmNiO₃) to achieve this behavior (B, Bottom). DOS, density of states. (C and D) LWIR images of samples mounted to hang off the edge of a heater stage, such that a temperature gradient is established from hot to cold. (C) A reference sample with a constant emissivity—in this case, a sapphire wafer—and (D) a ZDTE based on SmNiO₃. The color bar encodes the apparent temperature, obtained by assuming a particular set emissivity, ${\epsilon }_{set}$, which was chosen such that the sample region just below the heat stage appeared to be at 130 °C, which is the actual temperature at that point (see more discussion in Methods). For sapphire, there is a one-to-one relationship between temperature and thermally emitted power. Conversely, the ZDTE exhibits a constant emitted power over a range of temperatures, here ∼100 to 135 °C.