Moran Model of Spatial Alignment in Microbial Colonies

Abstract

We describe a spatial Moran model that captures mechanical interactions and directional growth in spatially extended populations. The model is analytically tractable and completely solvable under a mean-field approximation and can elucidate the mechanisms that drive the formation of population-level patterns. As an example we model a population of E. coli growing in a rectangular microfluidic trap. We show that spatial patterns can arise as a result of a tug-of-war between boundary effects and growth rate modulations due to cell-cell interactions: Cells align parallel to the long side of the trap when boundary effects dominate. However, when cell-cell interactions exceed a critical value, cells align orthogonally to the trap’s long side. This modeling approach and analysis can be extended to directionally-growing cells in a variety of domains to provide insight into how local and global interactions shape collective behavior.

Patterns emerge in collectives of interacting biological agents even in the absence of leaders or global signals. Collective motions of birds and fish arise from simple interactions between neighbors [1, 2], and gliding M. xanthus form coherently-moving clusters via steric interference [3]. Physical and chemical interactions can also drive biological pattern formation including mammalian coat markings [4–6], embryonic development [7, 8], and patterns in growing microbial colonies [9, 10]. Yet how local interactions drive collective, emergent behavior is not fully understood.

Recent experiments and agent-based simulations suggest that environmental geometry and physical interactions shape the global structures observed in microbial collectives [11–14]. In such populations cell growth is frequently directional: For instance, capsule-shaped bacteria grow along the major axis of their bodies, preferring directions with minimal physical resistance [10, 11, 15].

We introduce an analytically-tractable, spatial Moran model (SMM) that incorporates directional growth modulated by cell-cell interactions as a tool to understand the mechanisms that shape these spatial patterns. To illustrate this modeling approach, we describe a population of rod-shaped bacteria growing in an extended microfluidic trap [11, 12, 16]. In this model a cell’s orientation determines the directions in which it divides, while its location determines its growth rate. As physical growth requires the displacement of fewer cells towards the nearer boundary, we assume the rate of growth is higher in this direction.

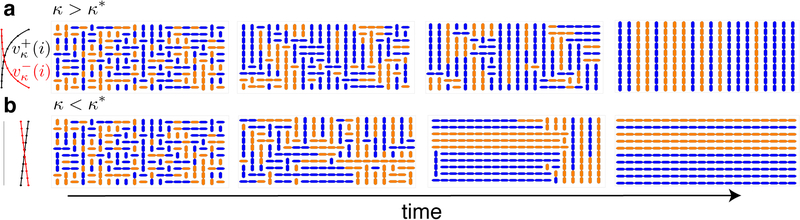
In this model a transition occurs at a critical value of cell–cell interactions: When cells do not strongly impact each other’s growth, the collective aligns parallel to the long side of the trap (see Fig. 2b). However, if cell-cell interactions become sufficiently strong, the collective aligns orthogonally to the trap’s long side (see Fig. 2a). The latter arrangement is observed experimentally, and our model suggests that modulations of growth-rate due to cell-cell interactions can drive the emergence of ordered states in spatially-extended populations [17].

FIG. 2.

Cells growing on a lattice according to a SMM. (a) Snapshots of the transient states and the all-vertical equilibrium for for κ > κ*. On the left, we show growth rates of vertically-oriented cells toward the upper and lower boundaries; (b) Same as (a) but for κ < κ*. See SI for movies.

SMMs have previously been used to model tumor initiation and growth and calculate fixation probabilities and first passage times for mutations [18–21]. However, earlier models did not include spatially-dependent, directional growth rates. Furthermore, while some analysis is possible, these systems are often intractable. We thus provide a flexible and tractable modeling approach that can be used to understand how the environment and cell-cell interactions shape the patterns observed in populations of cells.

Spatial Moran model (SMM).

We use the particular example of rod-shaped bacteria growing in a microfluidic trap to illustrate the general modeling approach and analysis. We model the rectangular microfluidic trap as an M × N lattice filled by vertically- or horizontally–oriented cells (see Fig. 1). For simplicity, we assume that initially the lattice is full, and cell orientation is random (starting with partly filled lattices results in the same steady-states; See SI). Cells grow at location–dependent rates, and upon division, a cell’s offspring replaces one of its neighbors. We denote by $v_{\kappa }^{\pm }(i)$ the growth rate of a vertical cell in the ith row toward the top (+) or bottom (−) boundary, and $h_{\kappa }^{\pm }(j)$ the growth rate of a horizontal cell in the jth column toward the right (+) or left (−) boundary (see Fig. 1). The growth rate of a vertical (horizontal) cell depends only on the row (column) in which it resides since we assume that growth rate is modulated by the population that lies between a cell and the closest boundary in the direction of growth. Growth rates are determined by a one-parameter function family, with the parameter κ ∈ [0, ∞) characterizing the population’s impact on growth. This family can be general, but we assume that growth rates are positive and satisfy three conditions: (1) There exists a λ ∈ (0, ∞) such that $v_{\kappa }^{\pm }(i)$, $h_{\kappa }^{\pm }(j)\to \text{λ}$ as κ → 0 for all i, j; (2) Maximal growth rates occur at the boundaries, $v_{\kappa }^{+}(M)=v_{\kappa }^{-}(1)=h_{\kappa }^{+}(N)=h_{\kappa }^{-}(1)=\text{λ}$; (3) $v_{\kappa }^{\pm }(i)$, $h_{\kappa }^{\pm }(j)$ decrease monotonically with distance from the boundary that maximizes their value. Condition (1) states that cells grow uniformly at rate λ in the absence of interactions (κ = 0). Conditions (2) and (3) reflect a cell’s tendency to grow toward the nearest boundary and growth rate dampening from cells obstructing growth in a certain direction (see Fig. 1). Unless otherwise noted, we used [22]

$$v_{\kappa }^{+}(i)=\text{λ}{e}^{(-\kappa (M-i))}{v}_{\kappa }^{-}(i)=\text{λ}{e}^{(-\kappa (i-1))}$$ (1a)

$$h_{\kappa }^{+}(j)=\text{λ}{e}^{(-\kappa (N-j))}{h}_{\kappa }^{-}(j)=\text{λ}{e}^{(-\kappa (j-1))}.$$ (1b)

FIG. 1.

In the SMM cell growth is directional and location-dependent: The vertical cell outlined in red can grow only upward or downward at a location-dependent rate. The red arrow indicates growth direction, so the cell above will be replaced by a descendant of the outlined cell. The population consists of two biochemically noninteracting strains for visualization: The initial color assignment is random, and daughter cells share the color of their mothers.

Cells grow by displacing their neighbors: In a small interval, Δt, a vertical (horizontal) cell at the ij-th site replaces a neighbor at (i ± 1)j (respectively i(j ± 1)) with a copy of itself with probability $v_{\kappa }^{\pm }(i)\Delta t$ (respectively $h_{\kappa }^{\pm }(j)\Delta t$). Divisions are independent across the population, and thus inter-event times are exponentially distributed. Only the division of an adjacent cell with the opposite orientation can alter the orientation at the ij-th site. Boundaries are absorbing: Divisions at the boundary producing descendants outside the trap result in no changes.

We note that the assumption that cell division results in replacing a neighbor with a copy of a dividing cell is not realistic. In a microfluidic trap, cell growth and division can result in a the displacement of multiple cells in the direction of growth. We can extend the model so that cell division causes displacement of the entire stack of cells between a dividing cell and the boundary. While such a model is more realistic, it is not analytically tractable as a birth at one location can affect distant parts of the population. However, a model that includes these long-range interactions displays similar behavior to our SMM (see SI Fig. S6). We therefore focus on the latter because of its simplicity and tractability.

Results.

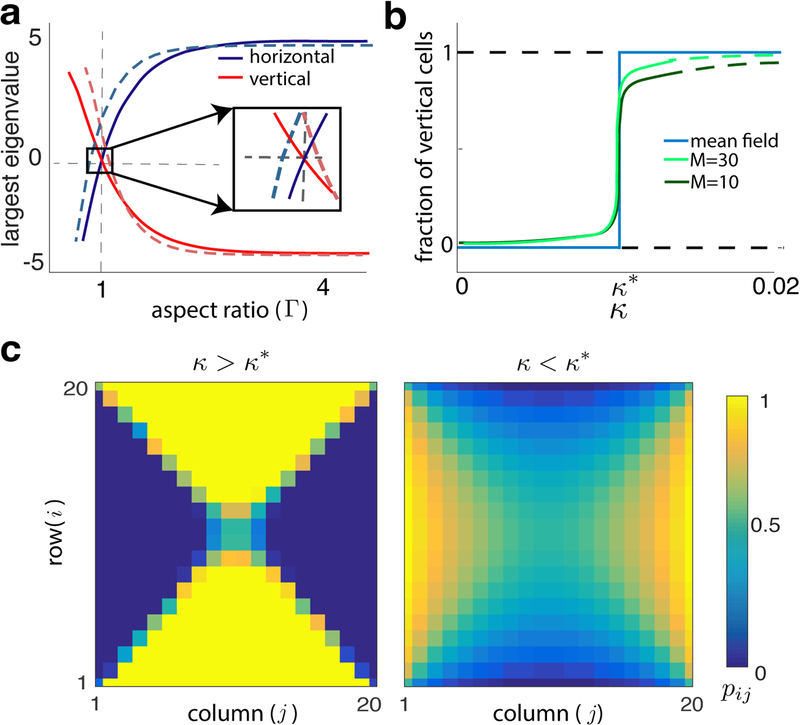
To understand the impact of trap geometry on collective bacterial cell alignment, we simulated the SMM using the Gillespie algorithm [23] on lattices with different aspect ratios, Г ≡ N/M, and different interaction parameters, κ. While the model has three parameters, κ, M, N, we focus on the parameters κ and Г, the latter of which defines the geometry of microfluidic traps. For κ sufficiently large, all initial conditions converge to the equilibrium where cells are orthogonal to the long side of the trap (see Fig. S2; for Г > 1, all cells vertical, for Г < 1, all cells horizontal). When Г = 1, the system reaches a quasi-equilibrium with cells orthogonal to the nearest boundary (see Fig. 3). This suggests that Г acts as a parameter for a transcritical-like bifurcation at Г = 1 where the horizontal and vertical equilibria exchange stability. We make this precise in the next section.

FIG. 3.

(a) Largest eigenvalue at all-vertical and all-horizontal equilibria (system sizes are M = 10, dashed, M = 100, solid). The two states lose stability at different points when M = 10, so that for a range of Г neither is stable. When M = 100 the equilibria lose stability nearly simultaneously at Г= 1. Here, κ = 0.1. (b) The fraction of vertical cells at equilibrium exhibits a sharp transition near κ* for fixed Г > 1 (Eq. (3), blue, and closed ME, Eq. (2), green). A secondary bifurcation in the all-vertical state occurs at κ > κ* (solid to dashed green line transition) (c) Steady states of the closed ME when Г = 1 for κ > κ* and κ < κ*.

Interestingly, when κ = 0, cells orient parallel to the long side of the trap (see Fig. 2b): When Г > 1 (Г < 1), the horizontal (vertical) equilibrium is stable. When Г = 1, symmetry again results in a saddle-like quasi-equilibrium, with cells parallel to the nearest boundary. Therefore, when cells divide at location-independent rates, (κ = 0) they approach an equilibrium opposite to that when growth is location-dependent (κ sufficiently large). We observed the second state experimentally, suggesting that such cell-cell interactions influence global structure. The model also suggests that a phase transition occurs at a critical value, κ*.

This exchange of stability between equilibria at κ* results from an interplay between boundary effects and growth rate variations. When κ = 0, all cells divide at equal rates, except for those orthogonal to a boundary. These are as likely to have a descendant within the trap as outside. However, more cells are likely to be orthogonal to the long boundary and to have a descendant outside the trap, than those orthogonal to the short boundary. Therefore, cells parallel to the long boundary have a higher effective growth rate and eventually fill the trap (see Fig. 2b). Conversely, when κ > κ*, cells parallel to the longer side of the trap will have more cells obstructing their growth than cells parallel to the short side. If κ is sufficiently large, the average growth rate of cells perpendicular to the long boundary will dominate, and these cells will fill the trap (see Fig. 2a). Even when κ > κ*, variations in growth rates across the lattice can be small: In a 20 × 10 lattice, κ* ~ 10⁻² (see below) and cell growth is reduced by half at ≈ 70 cell lengths.

Cell-cell interaction kernels satisfying conditions (1)-(3) will generally lead to the same qualitative results, and we obtain the critical values κ* analytically for a range of different functions below. As expected, κ* → 0 as lattice size grows, and near critical values in larger traps growth rates have smaller spatial variations than in smaller traps.

Master equation model.

To understand the dynamics of the SMM we develop a master equation (ME) describing the evolution of occupation probabilities at different lattice sites. Denote by n_ij ∈ {0, 1} the state of the ij-th site at time t, so that n_ij = 1 (n_ij = 0) corresponds to a site occupied by a vertical (horizontal) cell. The probabilities p_ij(t) = P(n_ij = 1 at time t) evolve according to the ME [24, 25],

$$\begin{gathered} \frac{d{p}_{ij}}{dt}=v_{\kappa }^{+}(i-1)p\left(n_{(i-1)j}=1,n_{ij}=0,t\right)+v_{\kappa }^{-}(i+1)p\left(n_{(i+1)j}=1,n_{ij}=0,t\right) \\ -h_{\kappa }^{+}(j-1)p\left(n_{i(j-1)}=0,n_{ij}=1,t\right)-h_{\kappa }^{-}(j+1)p\left(n_{i(j+1)}=0,n_{ij}=1,t\right), \end{gathered}$$ (2)

where p(n_ij, n_kl, t) are joint occupation probabilities at time t. The first two terms in Eq. (2) correspond to horizontal-to-vertical cell transitions through displacement by a descendant from a cell either above or below. The second two terms describe the opposite transition. Sites outside the lattice are unoccupied, so boundary conditions are determined by e.g. p(n_i(N+1) = 0, n_ij = 1, t) = p(n_0j = 1, n_ij = 0, t) = 0.

Eq. (2) is related to the Ising model as both describe the evolution of alignment probabilities on a lattice. However, the location-dependent growth rates lead to different interactions. While in our model no external field influences cell alignment [25], directional flow of media through the trap could have a similar effect.

The evolution of p_ij(t) depends on the joint probabilities p(n_ij, n_kl, t). The dynamics of the latter depend on the joint occupation probabilities at three or more sites leading to an infinite hierarchy of equations. Following a common approach [24, 25], we assume that the occupation states at neighboring sites are independent, p(n_ij = 1, n_kl = 1, t) = p_ij(t)p_kl(t), yielding a closed system of ODEs (see Eq. (S2)). The evolution of Eq. (2) and its approximation are both consistent with direct SMM simulations: When κ > κ* we observe an all-vertical state (p_ij ≈ 1) when Г > 1, and an all-horizontal state (p_ij(t) ≈ 0) when Г < 1. When Г = 1 orientations tend to be perpendicular to the closer boundary, and p_ij(t) ≈ 0.5 along the diagonals of the square lattice. In Fig. 3c we show the steady-state distribution of cell orientations when κ > κ* and κ < κ* for Г = 1 (See Fig. S2 for equilibria at different parameter values).

As in the SMM, equilibrium stability depends on Г and κ. Fig. 3a shows the largest real parts of the eigenvalues of the Jacobian of the closed ME at the all-vertical and all-horizontal equilibrium (p_ij = 1 and p_ij = 0 at all locations, respecitvely) for fixed κ > κ* as a function of Г. For Г > 1, the all-vertical state is stable. As Г crosses unity from above, the largest eigenvalue becomes positive, and the all-vertical state becomes unstable. The all-horizontal state exhibits the opposite behavior. For smaller lattices a saddle-like state (See Fig. 3c and Fig. S2) is stable over a range of Г (inset in Fig. 3a). Although discrete, Г thus behaves as a parameter for a transcritical bifurcation in which the all-vertical and all-horizontal states exchange stability at a saddle state.

Consistent with the SMM, when κ < κ*, the equilibria in the regimes Г < 1 and Г > 1 are opposite those when κ > κ* (See Fig. S2). Hence, κ acts as a second bifurcation parameter for the ME with the all-horizontal and all-vertical equilibria exchanging stability at critical value κ*: When Г > 1, and κ < κ* the stable equilibrium is predominantly horizontal. As κ grows, this equilibrium transitions to being predominantly vertical, and for some κ > κ*, it destabilizes and the all-vertical equilibrium becomes stable (see Figs. 3b and 4). For brevity, we refer to equilibria only as all-horizontal or all-vertical.

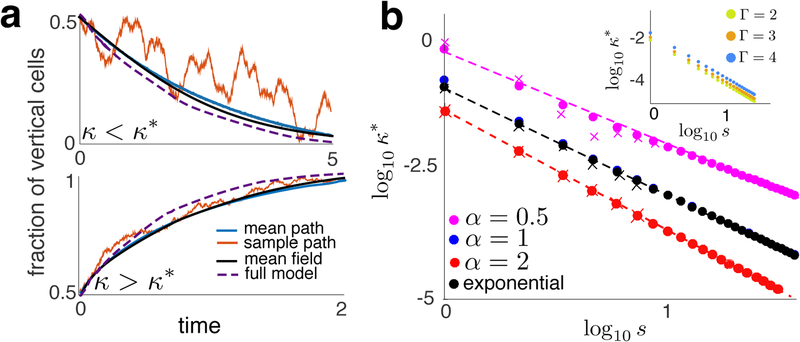
FIG. 4.

(a) Comparison of MF solutions with averages over realizations of the SMM (N = 20, M = 10). Also shown (dashed line) are averages over realizations of the long-range interaction model (see SI) to show that time scales between the models are comparable. (b) κ* as a function of s for different interaction kernels. Dots represent κ* values from Eq. (3). X’s were obtained numerically from simulations of the SMM using bisection. Dashed line were obtained using Eq. (4). Inset: κ* as a function of s for different aspect ratios, Г.

The transition in stability near κ = κ* and Г= 1 is driven by the same mechanisms as in the SMM: At Г = 1 the aspect ratio of the trap changes, while for κ > κ* location-dependent dampening of growth overcomes the loss of cells across the longer trap boundary.

Interestingly, solutions exhibit boundary layers for κ < κ* (see Fig. S2). This suggests a breakdown in the closed ME near the trap’s edges. Indeed, simulations of the SMM reveal high correlations between adjacent states near the short trap edge when κ < κ*. These correlations violate the assumptions used to obtain the ME, but decay rapidly away from the boundaries (see Fig. S3).

Mean field reduction.

We next average occupation states over the lattice to derive a simple mean field (MF) model that captures the behavior of the SMM, and allows us to compute κ* analytically. Let

$${\overline{v}}_{\kappa }\equiv \frac{1}{M}\sum _{i=1}^M{v}_{\kappa }^{+}(i),{\overline{h}}_{\kappa }\equiv \frac{1}{N}\sum _{j=1}^N{h}_{\kappa }^{+}(j),n\equiv \frac{1}{MN}\sum _{i,j}{p}_{ij},$$

so that n(t) is the fraction of vertical cells at time t, and ${\overline{v}}_{\kappa }$, ${\overline{h}}_{\kappa }$ are the average growth rates in the vertical, and horizontal directions, respectively. By symmetry, $v_{\kappa }^{-}$, and $h_{\kappa }^{-}$ also average to ${\overline{v}}_{\kappa }$, and ${\overline{h}}_{\kappa }$. Averaging the closed ME over all i, j shows that n obeys a logistic equation,

$$\frac{dn}{dt}=\underset{\mu (\kappa ,M,N)}{\underbrace{2\left({\overline{v}}_{\kappa }\left(1-\frac{1}{M}\right)-{\overline{h}}_{\kappa }\left(1-\frac{1}{N}\right)\right)}}n(1-n),$$ (3)

and n(t) = exp(μ(κ, M, N)t)/(1+exp(μ(κ, M, N)t). This agrees with the averaged solutions to Eq. (2) and SMM simulations averaged over realizations (see Fig. 4a).

The effective growth rate of the vertical cell fraction is thus $\mu (\kappa ,M,N)=2({\overline{v}}_{\kappa }(1-1/M)-{\overline{h}}_{\kappa }(1-1/N))$. When κ = 0, μ(0, M, N) = 2λ(1/N −1/M), and the effective growth rate is completely determined by boundary lengths. Cell-cell interactions modulate the effective growth rate as κ is increased. However, the system always has two equilibria corresponding to an all-vertical (n = 1) and all-horizontal (n = 0) orientation which exchange stability at N = M(Г = 1).

The two equilibria also exchange stability at a critical level of cell-cell interactions, κ*. For fixed M, N, this transition point satisfies μ(κ*, M, N) = 0. For 0 < κ < κ* and N < M (N > M) the state n = 1 (n = 0) is stable. When κ > κ* the difference in average growth rates, ${\overline{v}}_{\kappa }$, ${\overline{h}}_{\kappa }$, dominates boundary effects and the system reaches the opposite equilibrium. Unlike the ME, the MF model predicts a sharp transition between stable equilibria (see Fig. 3b) and no intermediate stable states. Although precise information about the underlying complex bifurcation structure is lost, the predicted equilibria and their stability agree with simulations of the SMM.

While a general closed form solution for κ* is not available, we can obtain approximate solutions for large domains and show how κ* scales with trap size for different interaction kernels. To reduce parameter number, we fix M and N and use a single parameter, s, to determine lattice dimensions as sM × sN. Expanding μ(κ, sM, sN) to second order in κ, and solving for κ* shows that for exponential kernels,

$${\kappa }^{*}~2/\left(MN{s}^2\right)~s^{-2}.$$ (4)

For interaction kernels that decay with the inverse power of distance from the boundary, $v_{\kappa }^{+}(i)=\text{λ}/\left(1+\kappa {(M-i)}^{\alpha }\right),\alpha \in (0,\infty )$,

$${\kappa }^{*}=\frac{(\alpha +1)(N-M)}{s^{\alpha +1}MN\left(N^{\alpha }-M^{\alpha }\right)}~s^{-(\alpha +1)}$$

for large s (See SI).

These asymptotic results agree with simulations (See Fig. 4b): κ* → 0 as s → ∞ at the predicted asymptotic rate. Interestingly, the exponential interaction kernel does not produce the strongest decay of κ* with s. The aspect ratio of the trap, Г, shifts the transition points, but does not change the scaling (See inset of Fig. 4b). In large traps even weak cell-cell interactions can cumulatively dominate boundary effects, and lead to steady-state cell alignments orthogonal to the trap’s long side.

Discussion.

We presented a general approach to modeling pattern formation in collectives of directionally-growing, mechanically interacting cells. We illustrated this approach using the example of a population of E. coli in an extended microfluidic trap. In this case cell loss across the trap’s boundary drives growth parallel to the long side of the rectangular domain, while cell-cell interactions drive orthogonal growth. We derived a logistic equation that approximates the full stochastic model, allowing us to analyze the phase transitions in detail.

Experiments with E. coli populations growing in open rectangular microfluidic traps show bands of a single strain of bacteria becoming orthogonal to the long edge (see Fig. 5). Our model suggests that cell growth rate modulation due to cell-cell interactions may drive this emergent order. Previous modeling approaches relying on more complex models have proposed complementary mechanisms [11, 12, 16, 26]).

FIG. 5.

A monolayer of E. Coli in an open microfluidic trap with cells aligned orthogonally to the trap’s long side. Colors represent distinct strains. Image is previously unpublished and taken from experiment run by RNA. Further experimental results can be seen in [11, 12, 16, 26].

Our model can be easily extended: We can include additional stochastic rules for more complex 2D, and even 3D, geometries. We can allow for stochastic switching of orientation, and allow for more than two orientations. Specifically, the phase transition we observed may depend on the discrete nature of the set of possible orientations, and may disappear if we allow for a continuum of orientations, as in the XY model [27, 28]. Furthermore, we can model multiple bacterial strains by increasing the number of occupational states at a lattice site. Including dynamical equations that describe cellular communication via quorum sensing molecules would then allow us to examine the interplay between cell distribution, communication, and growth that determine bacterial collective dynamics [29–32]. The proposed modeling approach may thus be applicable in a variety of contexts, including bacteria (B. subtilis, A. tumefaciens), fungi (fission yeast, A. nidulens), and plants (stem and root axis epidermal cells in A. thaliana) [33].