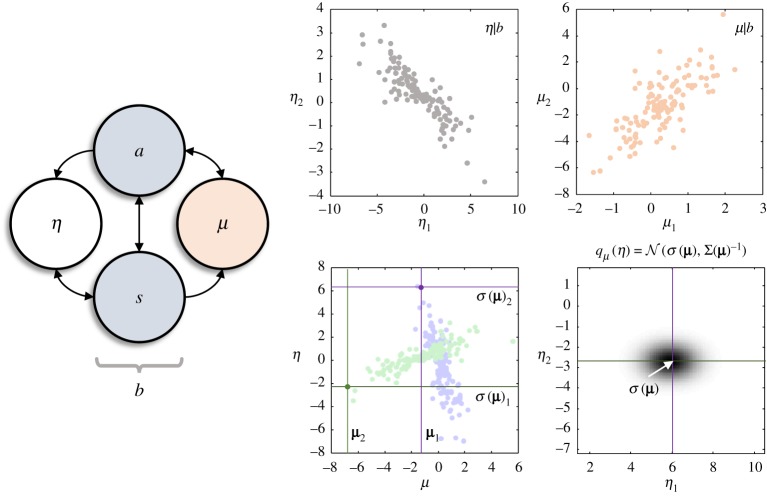
Figure 2.

Information geometry and Markov blankets. The schematic on the left specifies the minimal set of conditional independencies required to render a set of internal states (μ) independent of external states (η), conditioned upon the blanket states (b). These independencies come in two flavours: as indicated by the arrows, the active states (a) mediate the influence of the internal states on the external states but are not influenced by the external states. The sensory states (s) mediate influences in the opposite direction and are not influenced by internal states. The plots on the right aim to provide some intuition for the information geometry induced by a Markov blanket. The upper two plots were created by generating (one-dimensional) blanket states from a standard normal density. For each blanket state, we generated a pair of two-dimensional internal (μ₁, μ₂) and external states (η₁, η₂). These were generated from bivariate normal densities for the conditional probabilities of the internal and external states (p(μ|b) and p(η|b)), where the mean and covariance were linear functions of the blanket states. As the plots show, these sufficient statistics are scattered around a low-dimensional (statistical) manifold (of the same dimension as the blanket states) embedded within the higher-dimensional external and internal state-spaces. The lower left plot shows each pair of internal and external states (blue for the first element in each, and green for the second). Selecting the most likely internal state (μ) for a given blanket state, we see that we can map from this to the corresponding external state. The lower right plot shows how, equipping this mean with a covariance (under the Laplace assumption), we can associate an internal state with a density (q_μ(η)) over external states. (Online version in colour.)