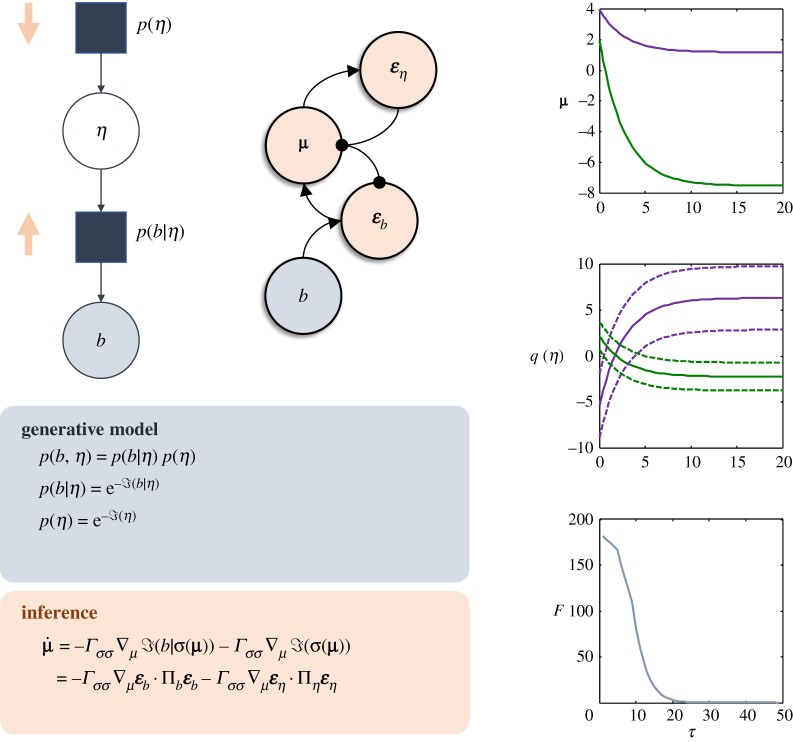
Figure 3.
Inferential dynamics and generative models. As outlined in the main text, the dynamics of the internal states of a system minimize the joint surprise of external and blanket states. Interpreting this joint density as a generative model, we can interpret gradient flows at non-equilibrium steady state in terms of variational inference, as shown here. The upper left graph illustrates the interpretation of the surprise in terms of a generative model (using a factor graph formalism) with a prior and a likelihood (squares). In the setting of variational inference, the dynamics that solve this inference problem may be framed as message passing, where the likelihood and prior each contribute local messages (pink arrows) that are combined to evaluate a (marginal) posterior probability. This provides an important point of contact with concepts like predictive coding [20] in theoretical neurobiology, as illustrated in the pink panel, and in the graphic on the right of the factor graph. This formulation uses the second-order Taylor expansion of surprise and interprets the difference between the predicted and observed blanket states as a prediction error (εb)—similarly for the difference between the prior and posterior expectations for the external states (εη). These errors drive updates in the internal states representing expected external states. This leads to a process of prediction error minimization. The plots on the right illustrate the dynamics of equations (3.6) and (3.8). If we initialize the expected internal states away from their mode under the steady state density, we see that they return to this. As they do so, the beliefs they represent become consistent with those shown in figure 2, and the free energy (F) difference from its steady-state value returns to zero. For readers who wish to gain an intuition for the dynamics of Markov-blanketed systems, a series of numerical demonstrations [21] may be accessed through academic software available at http://www.fil.ion.ucl.ac.uk/spm/software/. Typing DEM at the Matlab prompt will invoke a graphical user interface through which a range of simulations may be accessed and customized. This includes examples of practical applications of Bayesian mechanics in numerous domains. See also https://tejparr.github.io/Physics/Slides%20main.htm for a graphical introduction to these topics. (Online version in colour.)