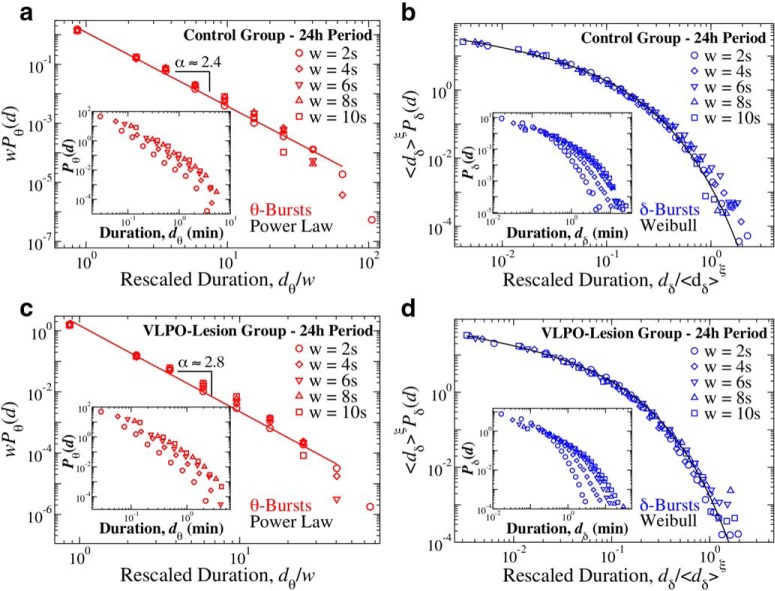
Figure 7.

Critical characteristics in the dynamics of bursts of dominant cortical rhythms are independent of the scale of analysis. Distribution of θ and δ-burst durations for different scales of observation defined by window sizes w (Fig. 1). a, Rescaled distribution of θ-burst durations for control rats over a 24 h period (pooled data). Distributions are rescaled by the window size w and consistently show the same power law behavior with α = 2.4 (red line), as proven by the data collapse. Inset, Distributions P_θ for different window sizes w (not rescaled). b, Rescaled distribution of δ-burst durations for control rats over a 24 h period (pooled data). Distributions are rescaled by 〈d_δ〉^ξ, where 〈d_δ〉 is the mean δ-burst duration and ξ = 1, and collapse onto a single function that is well described by a Weibull distribution f(d; λ, β) with λ= 6.18 and β = 0.72 (black line). Inset, Distributions P_δ for different window sizes (not rescaled). c, Rescaled distribution of θ burst durations for VLPO-lesioned rats over a 24 h period (pooled data). Distributions are rescaled by the window size w and consistently show the same power law behavior with α = 2.8 (red line), as proven by the data collapse. Inset, Distributions P_θ for different window sizes (not rescaled). d, Rescaled distribution of δ burst durations for VLPO-lesioned rats over a 24 h period (pooled data). Distributions are rescaled by 〈d_δ〉^ξ, with ξ = 1, and collapse onto a single function following a Weibull behavior f(d; λ, β) (black line) with λ = 15.20 and β = 0.74. Inset, Distributions P_δ for different window sizes (not rescaled). Results in all panels are obtained for fixed threshold Th = 1 on the ratio R_θδ (Fig. 1). Results are consistent when considering separately light and dark periods (Figs. 8, 9).