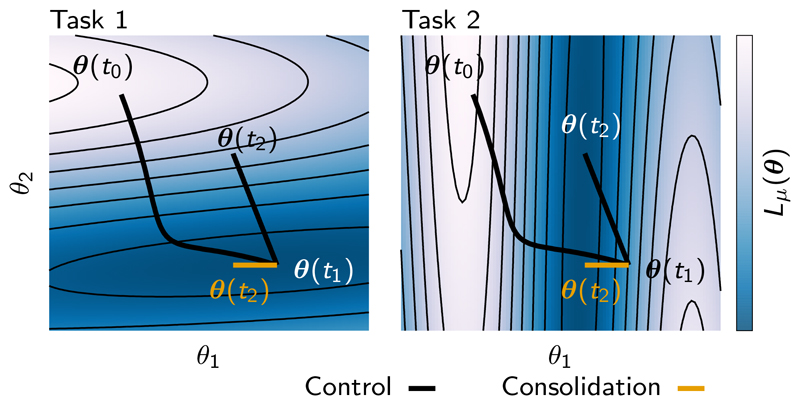
Figure 1.

Schematic illustration of parameter space trajectories and catastrophic forgetting. Solid lines correspond to parameter trajectories during training. Left and right panels correspond to the different loss functions defined by different tasks (Task 1 and Task 2). The value of each loss function L_μ is shown as a heat map. Gradient descent learning on Task 1 induces a motion in parameter space from from θ(t₀) to θ(t₁). Subsequent gradient descent dynamics on Task 2 yields a motion in parameter space from θ(t₁) to θ(t₂). This final point minimizes the loss on Task 2 at the expense of significantly increasing the loss on Task 1, thereby leading to catastrophic forgetting of Task 1. However, there does exist an alternate point θ(t₂), labelled in orange, that achieves a small loss for both tasks. In the following we show how to find this alternate point by determining that the component θ₂ was more important for solving Task 1 than θ₁ and then preventing θ₂ from changing much while solving Task 2. This leads to an online approach to avoiding catastrophic forgetting by consolidating changes in parameters that were important for solving past tasks, while allowing only the unimportant parameters to learn to solve future tasks.