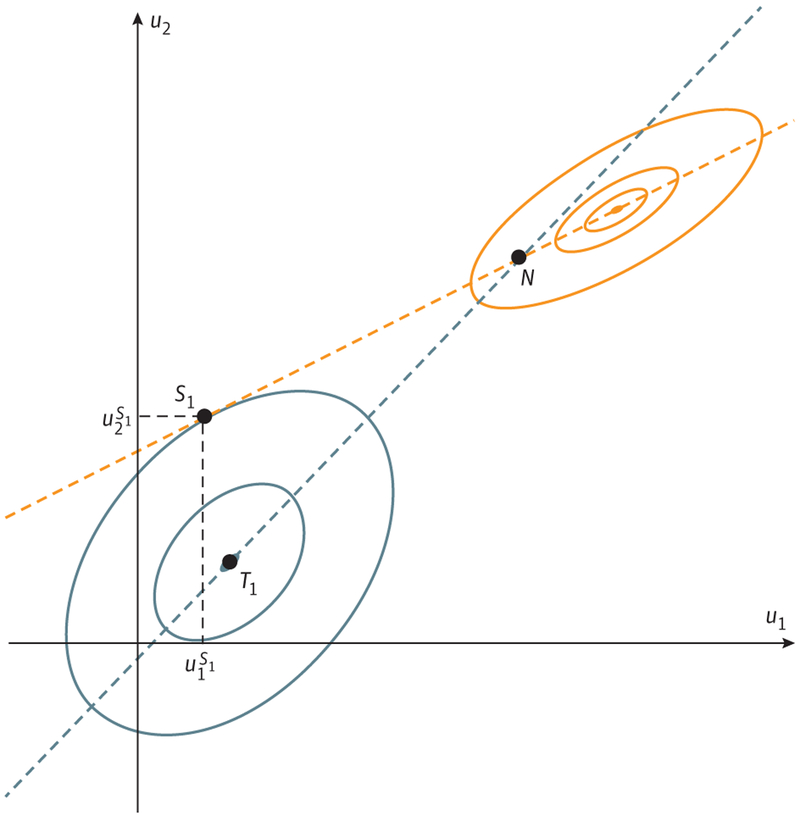
Figure 2. Nash and Stackelberg Equilibria.

We assume a 2-player game in which player 1 and player 2 choose actions u₁ and u₂ to maximize their payoffs J₁(u₁, u₂) and J₂(u₁, u₂), respectively. The graph shows level curves of payoffs J₁(u₁, u₂) (solid blue curves) and J₂(u₁, u₂) (solid orange curves) in the (u₁, u₂)-space. Player 1 would like to achieve point T₁ (his or her absolute maximum, known also as team optimum in game theory), and we investigate whether he or she can get close to this outcome when playing simultaneously with player 2 and when playing first. The blue dashed line denotes the best response of player 1 to any action of player 2 and the orange dashed line denotes the best response of player 2 to any action of player 1 (both obtained by maximizing a corresponding player’s payoff for any choice of the other player). If the players play simultaneously, the outcome lies at the intersection of the 2 best-response curves, the Nash equilibrium (N). However, if the physician (player 1) applies treatment with foreknowledge of the best-response curve of tumor cells, he or she can, as the leader, play the strategy u₁ with superscript S₁ based on that information. In contrast, the nonrational, follower cancer cells can only respond with the strategy on their best-response curve. The physician can anticipate this outcome; the cancer cells cannot. By exploiting his or her leadership role, the physician can both anticipate and steer the cancer cells’ resistance evolution toward a much better patient outcome corresponding to the point S₁, the Stackelberg equilibrium.