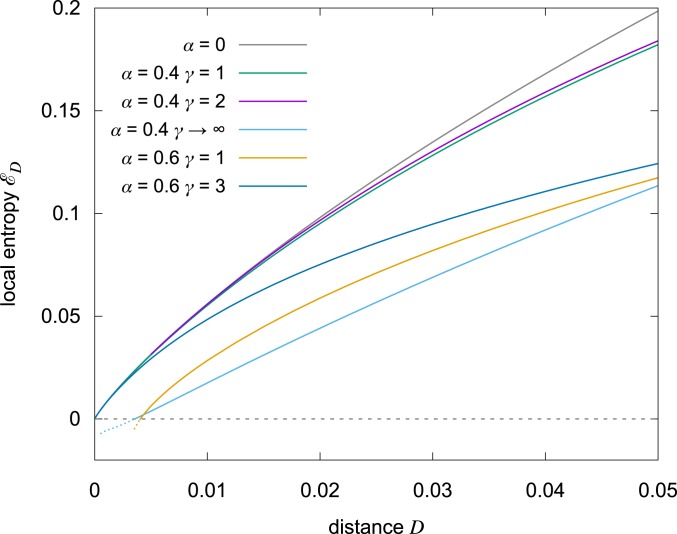
Fig. 3.

Average local entropy around a typical minimum of the ${\mathcal{L}}_{\mathrm{C}\mathrm{E}}$ loss for various values of $\alpha$ and $\gamma$. The gray upper curve, corresponding to $\alpha =0$, is an upper bound since in that case all configurations are solutions. For $\alpha =0.4$, the 2 curves with $\gamma =1$ and 2 nearly saturate the upper bound at small distances, revealing the presence of dense regions of solutions (HLE regions). There is a slight improvement for $\gamma =2$, but the curve at $\gamma \to \infty$ shows that the improvement cannot be monotonic: In that limit, the measure is dominated by isolated solutions. This is reflected by the gap at small $D$ in which the entropy becomes negative, signifying the absence of solutions in that range. For $\alpha =0.6$ we see that the curves are lower, as expected. We also see that for $\gamma =1$ there is a gap at small $D$, and that we need to get to $\gamma =3$ in order to find HLE regions.