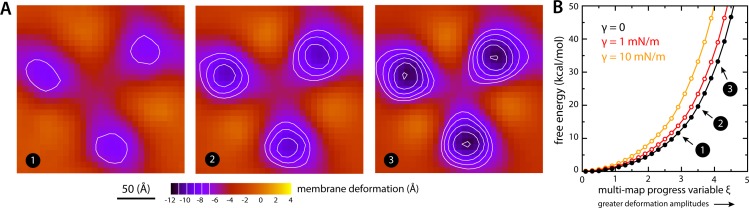
Figure 7. Estimate of the free-energy cost associated with the membrane deformation caused by all-inward GltPh, from direct potential-of-mean-force calculations.
(A) Simulated membrane deformation, in the absence of the protein, induced by application of the Multi-Map method in combination with umbrella sampling, for a coarse-grained POPC lipid bilayer at 298 K. The figure shows three deflection maps analogous to those shown in Figure 2A, that is calculated from trajectory data by averaging the Z coordinate of the bilayer mid-plane across the range of X and Y encompassed by the simulation box. The deflection maps shown correspond to three individual umbrella-sampling windows used in this free-energy calculation, differing in the amplitude of the perturbation that is induced in each case. Other trajectories/windows sample deformation amplitudes that are smaller or larger than those represented in the figure, that is, smaller or larger values of the Multi-Map variable. Each map reflects an average of 18 independent simulations of 1 μs each. (B) Potential-of-mean-force (PMF) curve for the morphological perturbation depicted in panel (A), as a function of the Multi-Map variable, that is, as a function of an increasing deformation amplitude. The free-energy values for the three configurations represented in panel (A) are indicated. PMF curves are also shown for two additional calculations based on umbrella-sampling simulations under an applied membrane tension, for the values indicated. Each of these PMF curves is an average of 18 independent calculations, each sampling 1 μs per window. Error bars for each curve average to about 0.6 kcal/mol.