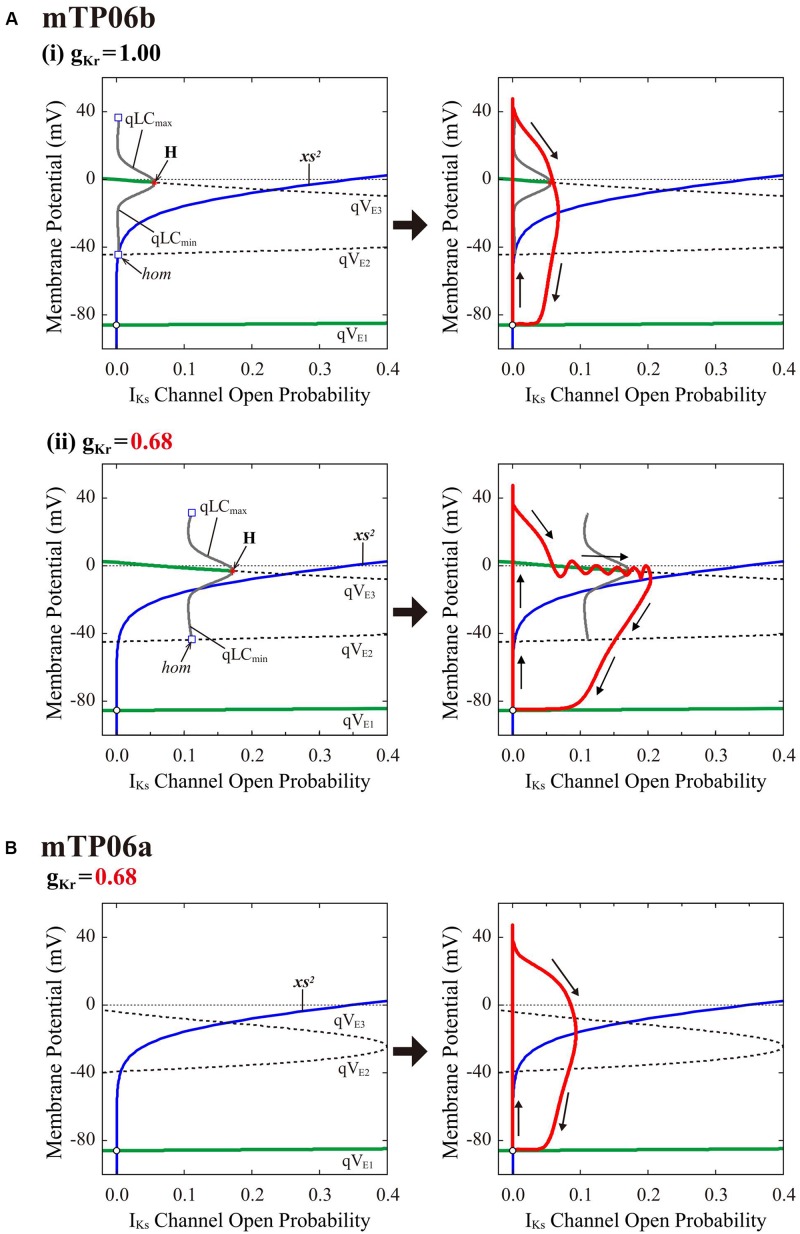
FIGURE 7.

Dynamical mechanisms of EAD initiation and termination determined by the slow-fast decomposition analysis for the mTP06 models. Shown are one-parameter bifurcation diagrams of quasi-equilibrium points (qEPs) and quasi-limit cycles (qLCs), where the steady-state branches as loci of V_m at qEPs (qV_E1–3) and periodic branches as the potential minimum (qLC_min) and maximum (qLC_max) of qLCs are depicted as functions of the square of the I_Ks activation gating variable (xs²), i.e., I_Ks channel open probability for the fast subsystems of the g_Kr-normal [A-(i), left] and g_Kr-reduced [A-(ii), left] mTP06b model and g_Kr-reduced mTP06a model (B, left). Other slow variables, Na_i and Ca_SR, were fixed at constant values: Na_i = 6 mM for all cases; Ca_SR was fixed at the value which was reached just before occurrence of the first EAD or the maximum values during AP phase 2 (when no EAD occurred), i.e., at 0.5 mM and 1.5 mM for the normal and g_Kr-reduced mTP06b model, respectively, and at 0.5 mM for the g_Kr-reduced mTP06a model. The steady-state branches consist of the stable (green solid lines) and unstable (black dashed lines) segments. The periodic branches (gray solid lines) are all unstable. The blue lines indicate the steady-state xs² curve. Trajectories of the full system (with the fixed Ca_SR and Na_i) are superimposed on the bifurcation diagrams for the fast subsystems (red lines in each right panel). The arrows indicate the directions of changes in the state variables. H, Hopf bifurcation; hom, homoclinic bifurcation.