Abstract.
Several autofocus algorithms based on the analysis of image sharpness have been proposed for microscopy applications. Since autofocus functions (AFs) are computed from several images captured at different lens positions, these algorithms are considered computationally intensive. With the aim of presenting the capabilities of dedicated hardware to speed-up the autofocus process, we discuss the implementation of four AFs using, respectively, a multicore central processing unit (CPU) architecture and a graphic processing unit (GPU) card. Throughout different experiments performed on 300 image stacks previously identified with tuberculosis bacilli, the proposed implementations have allowed for the acceleration of the computation time for some AFs up to 23 times with respect to the serial version. These results show that the optimal use of multicore CPU and GPUs can be used effectively for autofocus in real-time microscopy applications.
Keywords: autofocus functions, microscopy images, tuberculosis dataset, parallel computing, multicore central processing unit, graphic processing unit, nested parallelism, Hyper-Q
1. Introduction
In different applications involving microscopy systems, autofocus is a fundamental process for facilitating the analysis of a sample under study, improving the identification of particles of interest. A focus measure can be computed from images acquired at different lens positions; then the best focused position will correspond to where the focus measure of the image is a maximum.1 This mechanism, used in passive systems, is based on the analysis of the high-frequency content of a sequence of images acquired at different focal positions and the same field of view (FOV).2
In recent years, several algorithms have been proposed to determine the best focused image from a microscopy image stack. As discussed by various authors,3–7 the performance of an autofocus function (AF) depends on the microscopy modality and the image content, which has been classified as high-, medium-, and low-density background.7 A few examples are the following. Santos et al.3 and Osibote et al.4 determined that the autocorrelation method known as Vollath-4 provides the best performance for analytical fluorescent image cytometry studies and bright-field images of tuberculosis bacilli, respectively. Liu et al.5 and Kimura et al.6 realized an evaluation of autofocus methods for the analysis of blood smears and tuberculosis samples, respectively; both of them established that the variance of pixels was the most accurate method. Later, a comparison of 13 autofocus measures concluded that both Vollath-4 and mid-frequency discrete cosine transform (DCT) methods performed with the best accuracy for fluorescence images of tuberculosis bacilli.8 Furthermore, the results achieved by Wu et al.9 for the case of unstained transparent cell images acquired under a bright-field microscopy modality stated that the metrics known as normalized absolute variance, Vollath-5, and histogram entropy provided reliable focus positions. Derivative-based methods such as the well known Laplacian (LAP) and Tenengrad (TEN) have shown accurate enough results for the analysis of samples imaged under different microscopy modalities.8,10 Additional comparisons of past and current AFs in different image modalities are presented in Refs. 11–15.
By contrast, most autofocus algorithms are computationally intensive because they try to determine the high-frequency content of several images of the same FOV. Hence, their parallel implementation using dedicated hardware to reduce their processing times becomes necessary. Lei et al.,16 for example, proposed a dual-core approach to speed-up the autofocus process of a microscopic system; through the experiments, the authors achieved a maximum speed-up of around 1.75. Other authors have proposed the use of dedicated hardware architecture (Field Programmable Gate Array device) for the real-time autofocus process of conventional optical images;17,18 in particular, according to the experiments reported by Jin et al.,18 the implemented pixel-based autofocus system can process more than 150 frames per second (fps). In recent years, graphic processing units (GPUs) have played an important role in some microscopy applications; for example, some authors employed a GPU with 1334 cores to reconstruct frames, at a rate of 70 fps, in digital holographic microscopy.19 Recently, an autofocus method for microscopy images of sputum smears, which combines the finding of the optimal focus distance with an algorithm for extending the depth of field, was proposed.20 Although the proposal is an efficient low-cost implementation based on an embedded GPU system on chip architecture (256 GPU cores), the performance evaluation was realized over only 30 tuberculosis stacks.
Motivated by the aforementioned results, this paper discusses the parallel implementation of four AFs to speed-up the computation time in microscopy samples of tuberculosis bacilli, using a multicore central processing unit (multicore CPU) and a GPU board, respectively. The aim of this paper is to investigate the capabilities and limitations of such technologies to provide autofocused images in close to real-time microscopy applications. For this purpose, in addition to a comparison between multicore CPU and GPU architectures, we illustrate the way to improve their efficiency by the use of nested parallelism and Hyper-Q strategies to increase the speed-up of processing large datasets. We remark that previous works have not employed such strategies in microscopy applications, whereas previous GPUs implementations have obtained results based on small datasets. The organization of this document is as follows. Section 2 provides some characteristics of the tuberculosis image set, a brief mathematical treatment of the selected AFs, and the specifications of the hardware used in our experiments. In Sec. 3, we describe the parallelization of AFs under different configurations. Section 4 presents the performance of each function in terms of accuracy and computational time for both multicore CPU and GPU implementations, respectively. Section 5 presents a discussion of results, whereas in Sec. 6, some remarks and conclusions of this research are provided.
2. Materials and Methods
Several experiments were performed based on image stacks to analyze the automatic identification of Mycobacterium tuberculosis (TB).8 For this purpose, 300 stacks belonging to 10 patients previously diagnosed at Hospital Universitario Gregorio Marañón were imaged using a Nikon Eclipse 50i fluorescence microscope and a QImaging Retiga 2000R camera with a resolution of pixels. Each folder is formed by 20 images acquired at constant focus positions along the axis, with a constant step . For research purposes, these image stacks are available in Ref. 21.
As stated by the authors, the chosen constant step was small enough to be visually differentiable by a human observer. Hence, a single observer determined the optimal focus plane for each stack, which was used as the reference to evaluate the studied AFs. Figure 1 displays nine frames of a specific TB stack (stack 68). Note that the fourth image, starting from the top-left part, corresponds to the focused frame. Additional details about the dataset and the techniques used for the image acquisition process are described in Ref. 8.
Fig. 1.
Representative frames of a tuberculosis stack labeled as 68. Starting from the top-left, the fourth image corresponds to the focused frame.
The AFs used in our experiments were executed on a server (server K20) with an Intel® Xeon® CPU E5-2620 v2 2.10 GHz, 24 hyper-threading cores, 256 GB RAM, using Ubuntu 14.04 (64 bits) as the operating system. In addition, the server has a video card Tesla K20 with 13 multiprocessors, 2496 CUDA cores and 4 GB RAM.
2.1. Mathematical Description of Autofocus Functions
A desirable focus measure should be effective in terms of accuracy and speed. In this paper, four AFs, providing a high overall accuracy and a relatively high computational cost, were implemented in different parallel configurations. We remark that the metrics that were selected for this study have shown promising results under different microscopy modalities for the autofocus process of biological samples in preliminary studies.10,22
With the aim of presenting the mathematical description of such algorithms, consider an image from which we want to compute an AF , and whose intensity levels at coordinates , for and , respectively, are represented as . In the following description, the operator denotes the usual convolution operation, and denotes matrix transposition.
Vollath-4 (VOL4). By analyzing the influence of scene brightness and noise on focus measures, Vollath developed an autofocus measure based on an autocorrelation function, which is noise insensitive23 and it is expressed as follows:
| (1) |
Midfrequency-DCT (MDCT). By studying the influence of the DCT coefficients on the focus measure, the authors proposed a operator used to extract the central coefficient of the DCT, associated with a reliable focus.24 The MDCT focus measure can be calculated as
| (2) |
where
| (3) |
Tenengrad (TEN). The metric estimates the gradient of the image and then sums the square of all of the magnitudes greater than a given threshold value.25–27 In our implementation, we use Sobel’s operators and, to avoid the searching for an optimal threshold value, all of the resulting values are summed, such as
| (4) |
where represents the Sobel’s kernel denoted as
| (5) |
Laplacian (LAP). The algorithm convolves a discrete LAP mask with an input image to analyze its high-frequency content.28 The metric is expressed as follows:
| (6) |
where
| (7) |
To clarify the process of finding the best focused image by a given AF, let be the number of folders of a dataset and let be the number of images inside each folder. First, the intensity values of each read image are normalized to the range [0, 1]. Next, the AF is applied to each pixel of the normalized image and the value is accumulated and saved in a vector . Finally, the position of the maximum value of is found and saved in the resulting output vector of indexes (see Algorithm 1).
Algorithm 1.
Serial autofocus.
| Input: Parameters , . |
| Output: Indices of the best focused images. |
| 1: fordo |
| 2: fordo |
| 3: |
| 4: //Normalization |
| 5: fordo |
| 6: fordo |
| 7: |
| 8: end for |
| 9: end for |
| 10: //Autofocus function |
| 11: |
| 12: fordo |
| 13: fordo |
| 14: |
| 15: |
| 16: end for |
| 17: end for |
| 18: |
| 19: end for |
| 20: . |
| 21: end for |
3. Parallel Implementations
To accelerate the processing time of AFs, we developed two parallel implementations of the serial autofocus Algorithm 1: the first one uses a multicore CPU, whereas the second is executed on a GPU. Notice that in the normalization step of the algorithm we need only pixel-wise operations, applying an independent parallelism model,29 whereas to obtain the focused image, we need to accumulate all of the values that are returned by the AFs.
Some particularities of the AFs are described next. For an efficient implementation of VOL4, the summations in its mathematical expression can be implemented as large sums of the forms and ; since must be completed to the position [see Eq. (1)], a small sum of the form can be performed. At the end of the procedure, the result is computed as . The rest of the AFs requires a convolution process with a given kernel. In the following sections, the parallel implementations are detailed.
3.1. Multicore CPU
In a multicore CPU architecture, threads run independently on separate cores; furthermore, these threads share a physical memory.30 OpenMP is an application programming interface for shared-memory parallel programming.31 The “M” in OpenMP stands for “multiprocessing,” a term that is synonymous with shared-memory parallel computing. Thus OpenMP is designed for systems in which each thread or process can potentially have access to all available memory. OpenMP provides a set of pragma directives, which are used to specify parallel regions, to manage threads inside parallel regions, as well as to distribute for-loops in parallel, among others.
For the normalization step of our serial autofocus Algorithm 1, we only use the directive “#pragma omp for,” while for the AF we use the reduction directive “#pragma omp for reduction.” Note that, for the case of function VOL4, two reduction directives are necessary: one for the large sum and another for the small sum . Additionally, we use the directive to specify the number of threads to be launched in our program.
3.2. GPU
Nowadays, the GPU is used for general purpose computation. This parallel computing architecture contains multiple transistors for the arithmetic logic unit, based on the single instruction multiple threads programming model, which is exploited when multiple data are managed from one simple instruction in parallel, similar to single-instruction multiple data model.32,33 A language that is used for developing programs that are executed on a GPU is the compute unified device architecture (CUDA). CUDA is an extension of the C language that allows GPU code to be written in regular C. The host processor spawns multithread tasks (kernels) onto the GPU device. The GPU has its own internal scheduler that will then allocate the kernels to whatever GPU hardware is present.34
Following the conventional programming model in GPU, once an image is read we create memory in GPU; then the image is loaded in the GPU through a memory copy from the CPU to the GPU. In the current application, two kernel functions were implemented: one for the normalization step and another for the AF. For the AF, we implemented a parallel reduction using the interleaved pair strategy and dynamic shared memory.32 Hence, the size of the data is divided in thread blocks. In each thread block, a partial sum is computed using shared memory; then this partial sum is copied back to the CPU memory and summed in the CPU. Note that this last sum can be computed in parallel in the multicore CPU.
3.3. Nested Parallelism
After parallelization of both the normalization and AFs, it is possible to parallelize the external for-loops related to the number of folders and the number of images inside each folder . For this purpose, nested parallelism, which allows the management of a parallel region within other parallel regions, can be used. When a thread in a parallel region finds a new parallel construct, an additional set of threads is launched, and this thread becomes their master.35
To implement nested parallelism, we have developed three different versions of both multicore CPU and GPU implementations by parallelizing one of the for-loops in Algorithm 1. The first version consists of parallelizing the first external for-loop (see step 2 in Algorithm 1), which iterates over the number of images of each folder; the second one achieves the parallelization of the second external for-loop (see step 1 in Algorithm 1), which iterates over the number of folders in the dataset. Finally, the third version consists of the simultaneous parallelization of both for-loops.
3.4. Hyper-Q
In GPU Fermi architectures, when a CPU thread dispatches work into a CUDA stream, the work is joined into a single pipeline. Thus when several streams try to execute multiple-independent kernel functions, these generate false dependencies.36 Indeed, false dependencies are avoided using Hyper-Q.
Hyper-Q is a feature of NVIDIA GPUs with CUDA capability 3.5 (Kepler architecture) and higher. This feature adds more simultaneous hardware connections (32 work queues or streams) between the CPU and GPU, enabling CPU cores to simultaneously run more tasks on the GPU, maximizing the GPU utilization and, therefore, increasing the overall performance.32 Since this feature allows several kernel functions to be run in parallel on the GPU, we perform additional experiments using this capability for the current application.
4. Experimental Results
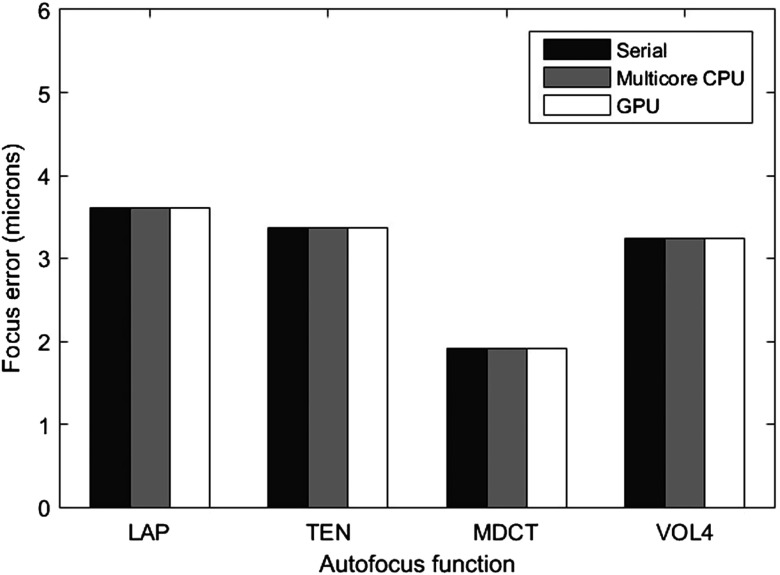
AFs were computed for each image stack, and the maximum value obtained by each function was considered the focus position; then the difference with respect to the reference focus point was considered the focus error. Figure 2 shows the mean accuracy error obtained by each studied metric along the tuberculosis dataset. The calculations were executed on a CPU (named as serial implementation), multicore CPU, and GPU to verify the consistency of results. In other words, due to the nonassociativity of floating-point operations in a parallel reduction, the floating-point computations may become nondeterministic and, therefore, nonreproducible.37 According to this graph, functions MDCT and VOL4 were capable of determining the focus position with the overall lowest error. Indeed, these results are in accordance with those reported by Mateos-Pérez et al.8
Fig. 2.
Mean accuracy error achieved by AFs computed along 300 tuberculosis image stacks.
On the other hand, when we run the VOL4 serial algorithm, the processing time of the image reading is about 25 s and the processing time of applying both the normalization and the AF is 159 s, giving a total time of around 184 s to process all 300 stacks. The remaining methods require, respectively, 218.33 s (LAP), 355.62 s (TEN), and 461.72 (MDCT) to complete the same task.
4.1. Multicore CPU and GPU Implementations
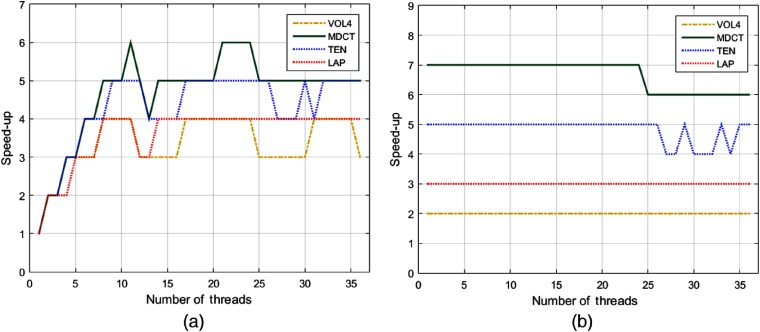
As an initial experiment, the performance of our parallel implementations for AFs was evaluated without nested parallelism. Hence, Fig. 3 displays the speed-ups of multicore CPU and GPU implementations, respectively, for a varying number of threads . In the first case [see Fig. 3(a)], we can see that the highest performance was reached by MDCT with (speed-up = 6); function TEN obtained its best performance with , while the remaining functions achieved a speed-up = 4 with . We note that the best performance is reached when is near the number of physical cores of the server (server K20 has 12 physical cores and 24 logical cores).
Fig. 3.
Evaluation of speed-ups for the studied AFs running on (a) a multicore CPU and (b) GPU, respectively.
In the GPU implementation, AFs showed an almost constant behavior for an increasing number of [see Fig. 3(b)], which demonstrates that the heaviest process is executed on GPU. Notice that MDCT achieved the highest speed-up, followed by TEN; functions LAP and VOL4 obtained a lower performance compared with the former methods.
4.2. Nested Parallelism Version
To evaluate our parallel implementations using nested parallelism, we executed multicore CPU and GPU versions by launching a varying number of threads. Specifically, we employed threads in the second external for-loop, threads in the first external for-loop, and threads in the inner for-loop (see as reference Algorithm 1); in each case, the best time obtained by every function and the number of threads employed were recorded. Tables 1 and 2 display the best execution times and maximum speed-ups achieved for multicore CPU and GPU implementations, respectively, under nested parallelism.
Table 1.
Processing time (s) for AFs in multicore CPU implementation using nested parallelism.
| Method | Multicore CPU (,,) | Max. speed-up | |||
|---|---|---|---|---|---|
| VOL4 | 51.24 | 20.17 | 15.68 | 15.92 | 12 |
| MDCT | 81.02 | 54.04 | 41.68 | 39.76 | 12 |
| TEN | 77.14 | 46.93 | 33.42 | 33.26 | 11 |
| LAP | 59.5 | 25.53 | 20.42 | 20.7 | 11 |
Note: Bold values represent the best execution time for each case.
Table 2.
Processing time (s) for AFs in GPU implementation using nested parallelism.
| Method | GPU (,,) | Max. speed-up | |||
|---|---|---|---|---|---|
| VOL4 | 78.43 | 51.8 | 40.87 | 40.57 | 6 |
| MDCT | 65.72 | 43.41 | 40.03 | 39.36 | 12 |
| TEN | 71.29 | 47.26 | 41.25 | 40.32 | 9 |
| LAP | 70.87 | 46.64 | 39.45 | 38.92 | 6 |
Note: Bold values represent the best execution time for each case.
As seen in Table 1, nested parallelism improves the overall processing time of AFs. In particular, VOL4 requires only 15.68 s to process the whole TB dataset (equivalent to 383 fps), while LAP takes around 20.42 s to complete the same task (294 fps). Furthermore, for this configuration, the maximum speed-up is achieved by functions VOL4 and MDCT, respectively.
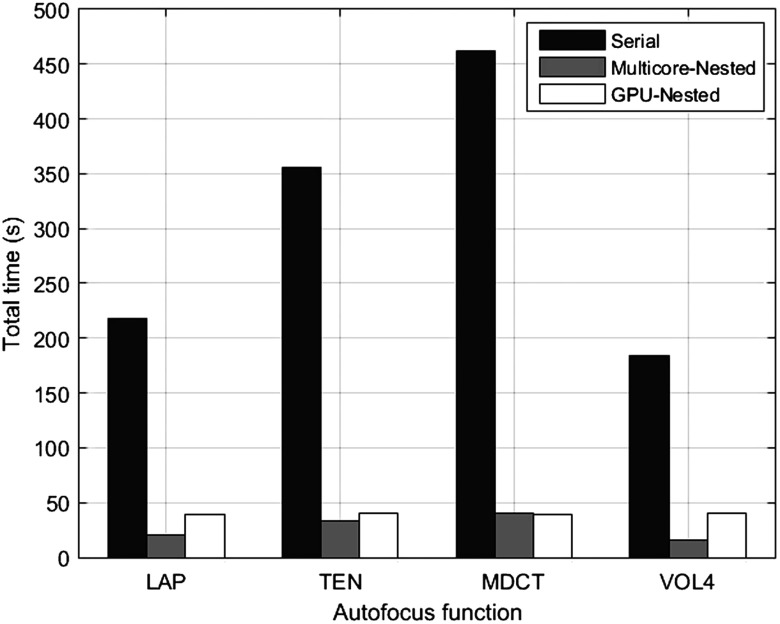
By contrast, as depicted in Table 2, the least execution time in the GPU was obtained by LAP, closely followed by MDCT; however, the maximum speed-up was achieved by this last function. The aforementioned results are summarized in Fig. 4, where the lowest processing times achieved by each parallel implementation are compared against the serial version.
Fig. 4.
Computation time to determine the focused positions of 300 stacks, with AFs running on CPU, multicore CPU-nested, and GPU-nested, respectively.
4.3. Hyper-Q Version
Until now, the higher performance of multicore CPU implementation with respect to the GPU version is evident. However, to take advantage of the Hyper-Q feature of Tesla K20 GPU, we divided the number of folders in equal parts as follows: two parts (2P), four parts (4P), and ten parts (10P), respectively. Thus each part was concurrently launched from a shell script. Table 3 shows the processing times, speed-ups, and GPU utilization percentage (GPU %) for function VOL4 with a varying number of folders. Notice that the speed-up increases as the GPU utilization percentage increases. In a similar way, Table 4 summarizes the maximum speed-ups for each metric by taking advantage of Hyper-Q. Some remarks on the aforementioned results are the following: function MDCT reached the maximum speed-up, with 95% of GPU utilization, followed by TEN. In addition, we found that with nested parallelism the GPU utilization is around 50%, while using Hyper-Q this percentage overcomes 90%, obtaining a better performance.
Table 3.
Results of GPU implementation using Hyper-Q, for VOL4 AF.
| GPU (,,) | Time (s) | Speed-up | GPU (%) | |
|---|---|---|---|---|
| (0,0,1) | 2P | 41.37 | 4 | 45 |
| 4P | 28.84 | 6 | 65 | |
| 10P | 25.20 | 7 | 82 | |
| (0,2,2) | 2P | 30.39 | 6 | 60 |
| 4P | 20.12 | 9 | 75 | |
| 10P | 22.42 | 8 | 85 | |
| (6,0,4) | 2P | 26.01 | 7 | 70 |
| 4P | 20.56 | 9 | 85 | |
| 10P | 17.50 | 11 | 93 | |
| (2,2,12) | 2P | 28.01 | 7 | 65 |
| 4P | 19.89 | 9 | 80 | |
| 10P | 24.84 | 7 | 63 |
Note: Bold values represent the maximum speed-up.
Table 4.
Maximum speed-up of GPU implementation using Hyper-Q, for each AF.
| Method | GPU (,,) | Time (s) | Speed-up | GPU (%) | |
|---|---|---|---|---|---|
| VOL4 | (6,0,4) | 10P | 17.5 | 11 | 93 |
| MDCT | (4,0,2) | 10P | 20.26 | 23 | 95 |
| TEN | (2,1,1) | 10P | 21.33 | 17 | 90 |
| LAP | (4,0,4) | 10P | 19.79 | 11 | 92 |
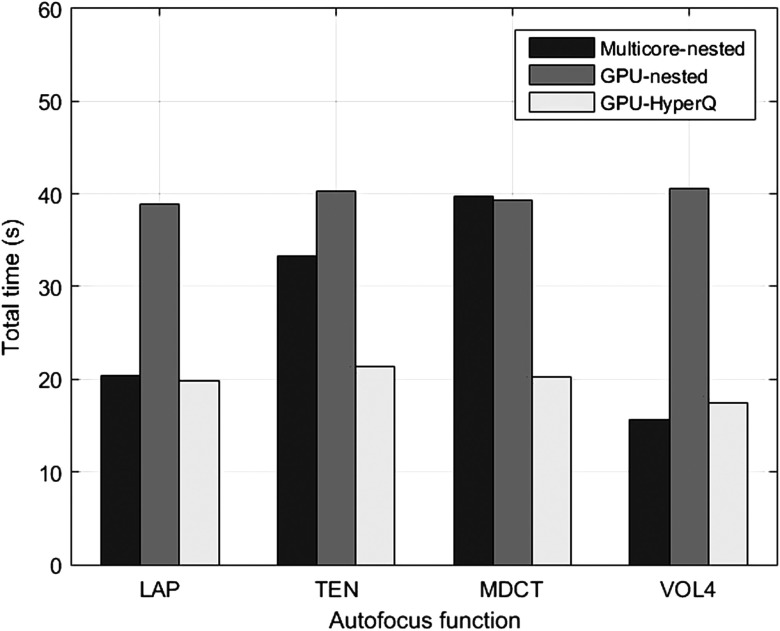
Finally, with the aim of comparing the best performance for every parallel implementation, Fig. 5 displays the best results obtained for each method, using nested parallelism and Hyper-Q, respectively. According to these results, the use of multicore CPU with nested parallelism provides the best results for the autocorrelation function VOL4. GPU with nested parallelism is not as competitive as the multicore version. However, the performance of functions based on convolution masks like MDCT and TEN was considerably improved using GPU and Hyper-Q. For practical applications and future comparisons, a demo of our parallel implementations is available in Ref. 38.
Fig. 5.
Computation time to determine the focused image of 300 stacks using different parallel implementations on multicore CPU and GPU.
5. Discussion
In our first experiment, AFs were executed on multicore CPU and independently on GPU, for a varying number of threads. According to the experiments, MDCT achieved the maximum performance on multicore CPU (speed-up = 6, with ), as well as on GPU (speed-up = 7, with ). In GPU, AFs showed an almost constant behavior for an increasing number of .
As shown by our results, nested parallelism improves the overall processing time of AFs. In particular under multicore CPU configuration, VOL4 requires only 15.68 s to process the whole TB dataset, achieving the maximum speed-up of 12. Furthermore, the best execution time in GPU was obtained by function LAP; however, the maximum speed-up was achieved by MDCT.
The Hyper-Q feature of Tesla K20 card allowed us to optimize the GPU utilization percentage, diminishing the processing time of AFs. In this sense, function MDCT reached a speed-up of 23, when the GPU utilization was around 95%. In addition, it was possible to determine that in nested parallelism the GPU utilization was around 50%, while using Hyper-Q, this percentage overcame 90%, obtaining a better performance.
6. Conclusions
Throughout this paper, we have compared the parallel implementations of four autofocus algorithms using a multicore CPU and a GPU, respectively. The AFs that were selected for these implementations have provided in previous studies accurate enough results under different microscopy modalities, at a relatively high computational cost. For our experiments, a large data set formed by 300 stacks of Mycobacterium tuberculosis was analyzed.
In the case of multicore CPU without nested parallelism, we observed that the best performance is achieved when we adjust the number of launched threads near the number of physical cores of the CPU. However, the efficiency of multicore CPU and GPU was improved by the use of nested parallelism and Hyper-Q strategies, respectively. Indeed, these strategies have not been used in previous works related to microscopy applications.
We found that the use of multicore CPU with nested parallelism provides better results than the GPU-Nested implementation (specially for the autocorrelation function VOL4). However, a maximum GPU utilization percentage is achieved using the Hyper-Q feature, reaching a processing rate of 296 fps for function MDCT. The processing times obtained in this study are considerably superior to those reported in the current literature; hence, our parallel implementations can be useful tools for close to real-time microscopy applications.
Acknowledgments
The authors would like to thank the Hospital Universitario Gregorio Marañón for providing the data set used in this study.
Biographies
Juan C. Valdiviezo-N is a researcher at Centro de Investigación en Ciencias de Información Geoespacial, México. He received his PhD in Optics from the National Institute of Astrophysics, Optics, and Electronics, México, in 2012. He is a member of the National Research System (SNI-CONACYT). His current research interests include image processing, pattern recognition, computer vision, and remote sensing applications.
Francisco J. Hernandez-Lopez received his BE degree in computer systems engineering from the San Luis Potosi Institute of Technology, Mexico, in 2005. He received his MSc and DSc degrees in Computer Science from the Center for Research in Mathematics (CIMAT), Mexico, in 2009 and 2014 respectively. Since 2014, he is in the Computer Science Department at the CIMAT, Merida, Mexico. Main interest areas: computer vision, image and video processing, parallel computing, and machine learning.
Carina Toxqui-Quitl is an assistant professor at the Polytechnic University of Tulancingo. She received her BS degree in the Puebla Autonomous University, Mexico, in 2004. And her MS and PhD degrees in Optics from the National Institute of Astrophysics, Optics and Electronics in 2006 and 2010, respectively. Her current research areas include image moments, depth of focus extension, wavelet analysis, and computer vision.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Subbarao M., Tyan J. K., “Selecting the optimal focus measure for autofocusing and depth-from-focus,” IEEE Trans. Pattern Anal. Mach. Intell. 20(8), 864–870 (1998). 10.1109/34.709612 [DOI] [Google Scholar]
- 2.Shah M. I., Mishra S., Rout C., “Establishment of hybridized focus measure functions as a universal method for autofocusing,” J. Biomed. Opt. 22(12), 126004 (2017). 10.1117/1.JBO.22.12.126004 [DOI] [PubMed] [Google Scholar]
- 3.Santos A., et al. , “Evaluation of autofocus functions in molecular cytogenetic analysis,” J. Microsc. 188(3), 264–272 (1997). 10.1046/j.1365-2818.1997.2630819.x [DOI] [PubMed] [Google Scholar]
- 4.Osibote O. A., et al. , “Automated focusing in bright-field microscopy for tuberculosis detection,” J. Microsc. 240(2), 155–163 (2010). 10.1111/jmi.2010.240.issue-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu X. Y., Wang W. H., Sun Y., “Dynamic evaluation of autofocusing for automated microscopic analysis of blood smear and pap smear,” J. Microsc. 227(1), 15–23 (2007). 10.1111/jmi.2007.227.issue-1 [DOI] [PubMed] [Google Scholar]
- 6.Kimura A., et al. , “Evaluation of autofocus functions of conventional sputum smear microscopy for tuberculosis,” in Proc. IEEE Conf. EMBC, pp. 3041–3044 (2010). 10.1109/IEMBS.2010.5626143 [DOI] [PubMed] [Google Scholar]
- 7.Gu C. C., et al. , “Region sampling for robust and rapid autofocus in microscope,” Microsc. Res. Tech. 78(5), 382–390 (2015). 10.1002/jemt.v78.5 [DOI] [PubMed] [Google Scholar]
- 8.Mateos-Pérez J. M., et al. , “Comparative evaluation of autofocus algorithms for a real-time system for automatic detection of Mycobacterium tuberculosis,” J. Cytometry Part A 81(3), 213–221 (2012). 10.1002/cyto.a.v81a.3 [DOI] [PubMed] [Google Scholar]
- 9.Wu S. Y., Dugan N., Hennelly B. M., “Investigation of autofocus algorithms for bright-field microscopy of unstained cells,” Proc. SPIE 9131, 91310T (2014). 10.1117/12.2051944 [DOI] [Google Scholar]
- 10.Redondo R., et al. , “Autofocus evaluation for bright-field microscopy pathology,” J. Biomed. Opt. 17(3), 036008 (2012). 10.1117/1.JBO.17.3.036008 [DOI] [PubMed] [Google Scholar]
- 11.Mir H., Xu P., Beek P. V., “An extensive empirical evaluation of focus measures for digital photography,” Proc. SPIE 9023, 90230I (2014). 10.1117/12.2042350 [DOI] [Google Scholar]
- 12.Fu G., Cao Y., Lu M., “A fast auto-focusing method of microscopic imaging based on an improved MCS algorithm,” J. Innov. Opt. Health Sci. 8(5), 1550020 (2015). 10.1142/S1793545815500200 [DOI] [Google Scholar]
- 13.Panicker R. O., et al. , “A review of automatic methods based on image processing techniques for tuberculosis detection from microscopic sputum smear images,” J. Med. Syst. 40(17), 1–13 (2016). 10.1007/s10916-015-0388-y [DOI] [PubMed] [Google Scholar]
- 14.Zhang Z., et al. , “Focus and blurriness measure using reorganized DCT coefficients for autofocus applications,” IEEE Trans. Circuits Syst. Video Technol. 28(1), 15–30 (2016). 10.1109/TCSVT.2016.2602308 [DOI] [Google Scholar]
- 15.Xia X., et al. , “Evaluation of focus measures for the autofocus of line scan cameras,” Optik 127(19), 7762–7775 (2016). 10.1016/j.ijleo.2016.05.114 [DOI] [Google Scholar]
- 16.Lei Z., et al. , “Real-time multi-core parallel image sharpness evaluation algorithm for high resolution CCD/CMOS based digital microscope autofocus imaging system,” Proc. SPIE 7384, 738415 (2009). 10.1117/12.835288 [DOI] [Google Scholar]
- 17.Miaofen Z., et al. , “Image focusing system based on FPGA,” in Int. Symp. Comput., Commun. and Autom., vol. 1, pp. 415–148 (2010). 10.1109/3CA.2010.5533783 [DOI] [Google Scholar]
- 18.Jin S., et al. , “A dedicated hardware architecture for real-time auto-focusing using an FPGA,” Mach. Vision Appl. 21, 727–734 (2010) 10.1007/s00138-009-0190-2 [DOI] [Google Scholar]
- 19.Dogar M., IIhan H. A., Ozcan M., “Real-time, auto-focusing digital holographic microscope using graphics processors,” Rev. Sci. Instrum. 84, 083704 (2013). 10.1063/1.4818285 [DOI] [PubMed] [Google Scholar]
- 20.Castillo-Secilla J. M., et al. , “Autofocus method for automated microscopy using embedded GPUs,” Biomed. Opt. Express 8(3), 1731–1740 (2017). 10.1364/BOE.8.001731 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mateos-Pérez J. M., et al. , “Comparative evaluation of autofocus algorithms for a real-time system for automatic detection of Mycobacterium tuberculosis,” J. Quant. Cell Sci. 81A(3), 213–221 (2012). 10.1002/cyto.a.22020 [DOI] [PubMed] [Google Scholar]
- 22.Valdiviezo J. C., et al. , “Autofocusing in microscopy systems using graphics processing units,” Proc. SPIE 8856, 88562K (2013). 10.1117/12.2024967 [DOI] [Google Scholar]
- 23.Vollath D., “The influence of the scene parameters and of noise on the behavior of automatic focusing algorithms,” J. Microsc. 151(2), 133–146 (1988). 10.1111/jmi.1988.151.issue-2 [DOI] [Google Scholar]
- 24.Lee S. Y., et al. , “Enhanced autofocus algorithm using robust focus measure and fuzzy reasoning,” IEEE Trans. Circuits Syst. Video Technol. 18(9), 1237–1246 (2008). 10.1109/TCSVT.2008.924105 [DOI] [Google Scholar]
- 25.Tenenbaum J. M., “Accommodation in computer vision,” PhD thesis, Department of Computer Science, Stanford University, Stanford, California (1970). [Google Scholar]
- 26.Schlang J. F., et al. , “Implementation of automatic focusing algorithms for a computer vision system with camera control,” Tech. Rep. CMU–RI–TR–83–14, Carnegie Mellon University (1983).
- 27.Krotkov E., “Focusing,” Int. J. Comput. Vision 1(3), 223–237 (1987). 10.1007/BF00127822 [DOI] [Google Scholar]
- 28.Russell M. J., Douglas T. S., “Evaluation of autofocus algorithms for tuberculosis microscopy,” in Proc. IEEE Conf. EMBS, pp. 3489–3492 (2007). 10.1109/IEMBS.2007.4353082 [DOI] [PubMed] [Google Scholar]
- 29.Sutter H., Larus J., “Software and the concurrency revolution,” Queue-Multiprocessors 3(7), 54–62 (2005). 10.1145/1095408 [DOI] [Google Scholar]
- 30.Akhter S., Roberts J., Multi-Core Programming, Intel Press, Hillsboro, Oregon: (2006). [Google Scholar]
- 31.Pacheco P., An Introduction to Parallel Programming, 1st ed., Morgan Kaufmann Publishers Inc., San Francisco, California: (2011). [Google Scholar]
- 32.Cheng J., Grossman M., McKercher T., Professional CUDA C Programming, Wrox Press Ltd., United Kingdom: (2014). [Google Scholar]
- 33.Kirk D. B., Hwu W. W., Programming Massively Parallel Processors: A Hands-on Approach Applications of GPU Computing Series, 1st ed., Morgan Kaufmann Publishers Inc., San Francisco, California: (2010). [Google Scholar]
- 34.Cook S., Cuda Programming: A Developer’s Guide to Parallel Computing with GPUs, Morgan Kaufmann Publishers Inc., San Francisco, California: (2012). [Google Scholar]
- 35.Chapman B., et al. , Using OpenMP: Portable Shared Memory Parallel Programming, MIT Press, Cambridge, Massachusetts: (2008). [Google Scholar]
- 36.Bradley T., “Hyper-Q example,” 2013, http://developer.download.nvidia.com/compute/DevZone/C/htmlx64/6Advanced/simpleHyperQ/doc/HyperQ.pdf.
- 37.Collange S., et al. , “Numerical reproducibility for the parallel reduction on multi- and many-core architectures,” Parallel Comput. 49, 83–97 (2015). 10.1016/j.parco.2015.09.001 [DOI] [Google Scholar]
- 38.Valdiviezo-N J. C., Hernández-L F. J., Toxqui-Q C., “Parallel implementations to accelerate the autofocus process in microscopy applications,” 2019, https://www.cimat.mx/~fcoj23/Autofocus/AFStacks.html. [DOI] [PMC free article] [PubMed]