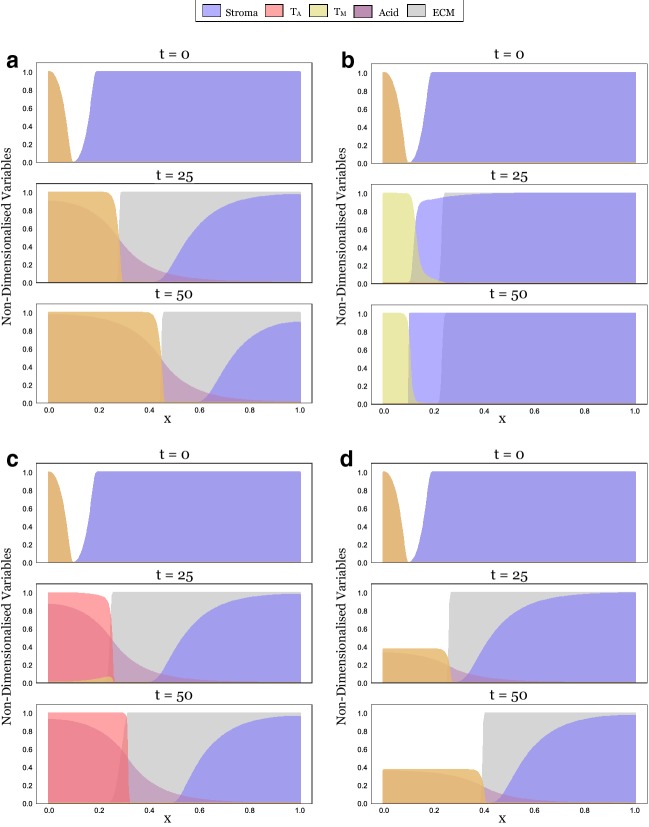
Fig. 5.

Simulations illustrating the four different scenarios that can occur depending on the inter-species competition between $T_{\mathrm{A}}$ and $T_{\mathrm{M}}$. Panels correspond to the locations in the competition parameter space marked in Fig. 4a (1:A, 2:B, 3:C, 4:D). a$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(0,0)$. At $t=0$, the tumour begins as a mixture of acid-producing (red) and matrix-degrading cells (yellow) on the left-hand side of the domain (appearing orange due to the mixture of the colours). It is constrained by a mixture of stroma (blue) and ECM (grey) on the right-hand side (appearing as dark blue). Since inter-species competition is weak, the tumour populations can coexist and combine their traits, allowing them to invade rapidly ($t=25$ and $t=50$). b$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(1.2,0.7)$. In contrast, when $T_{\mathrm{M}}$ dominates over $T_{\mathrm{A}}$, it drives $T_{\mathrm{A}}$ to extinction and no invasion takes place. c$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(0.7,1.2)$. $T_{\mathrm{A}}$ dominates over $T_{\mathrm{M}}$. While invasion eventually stops due to a lack of ECM degradation, the tumour initially invades thanks to a small population of $T_{\mathrm{M}}$ persisting at the tumour edge (appearing in orange at $t=25$). d$(c_{\mathrm{M},\mathrm{A}},c_{\mathrm{A},\mathrm{M}})=(1.7,1.7)$. Mutual exclusion of $T_{\mathrm{A}}$ and $T_{\mathrm{M}}$. When seeded at equal densities, the two populations will invade as shown, but the invading front is not stable. If a small perturbation is introduced, the two populations will separate and invasion will halt (Fig. 8)