Structural Basis of Enhanced Facilitated Diffusion of DNA-Binding Protein in Crowded Cellular Milieu

Abstract

Although the fast association between DNA-binding proteins (DBPs) and DNA is explained by a facilitated diffusion mechanism, in which DBPs adopt a weighted combination of three-dimensional diffusion and one-dimensional (1D) sliding and hopping modes of transportation, the role of cellular environment that contains many nonspecifically interacting proteins and other biomolecules is mostly overlooked. By performing large-scale computational simulations with an appropriately tuned model of protein and DNA in the presence of nonspecifically interacting bulk and DNA-bound crowders (genomic crowders), we demonstrate the structural basis of the enhanced facilitated diffusion of DBPs inside a crowded cellular milieu through, to our knowledge, novel 1D scanning mechanisms. In this one-dimensional scanning mode, the protein can float along the DNA under the influence of nonspecific interactions of bulk crowder molecules. The search mode is distinctly different compared to usual 1D sliding and hopping dynamics in which protein diffusion is regulated by the DNA electrostatics. In contrast, the presence of genomic crowders expedites the target search process by transporting the protein over DNA segments through the formation of a transient protein-crowder bridged complex. By analyzing the ruggedness of the associated potential energy landscape, we underpin the molecular origin of the kinetic advantages of these search modes and show that they successfully explain the experimentally observed acceleration of facilitated diffusion of DBPs by molecular crowding agents and crowder-concentration-dependent enzymatic activity of transcription factors. Our findings provide crucial insights into gene regulation kinetics inside the crowded cellular milieu.

Significance

10–40% of the intracellular volume is occupied by proteins, and other biomolecules, collectively known as macromolecular crowders. Their presence has been found to promote faster translocation of DNA-binding proteins (DBPs) during the search of their target DNA sites for crucial cellular processes. Using molecular simulations, we probe the underlying structural basis and underscore the existence of, to our knowledge, novel DNA scanning mechanisms actuated by nonspecific interactions of crowder proteins. We show that the observed search modes are kinetically beneficial and can successfully explain the acceleration of facilitated diffusion of DBPs by molecular crowding agents and crowder-concentration-dependent enzymatic activity of transcription factors. Our study sheds new light on the long-standing facilitated diffusion problem of DBPs in the crowded cellular environment for regulating gene expression.

Introduction

The rapid and efficient association of DNA-binding proteins (DBPs) to their target sites on genomic DNA fuels important biological processes such as gene expression, transcription, DNA damage repair, etc. (1, 2, 3). The fast kinetics is achieved through a weighted proportion of one- and three-dimensional (3D) diffusion (4,5) of the DBPs. During one-dimensional (1D) diffusion, proteins either slide along the helical pitch of the DNA or perform series of dissociation and reassociation events of short life spans (“hopping”) along the DNA contour. Furthermore, the proteins facilitate the search process via intersegmental “jumps” (6,7) between nearby DNA segments and are thereby able to bypass the scanning of several DNA bases. Flanking DNA sequence around the target DNA site has also been found to modulate the search process by altering the funnel-shaped protein-DNA binding energy landscape (8). These multifaceted search mechanisms have been captured in vitro via different spectroscopic approaches (9, 10, 11, 12, 13) and also through in silico models and simulations (14, 15, 16, 17, 18, 19, 20, 21, 22, 23) at the single-molecule level. The in vivo condition is, however, entirely different because of the presence of an astounding concentration (∼100–300 mg/mL) of dissolved macromolecules (24,25). This means 10–40% of the total intracellular volume is occupied by the macromolecules that cause ∼5–10 times high viscosity in the cellular medium compared to the laboratory buffer solutions. Furthermore, most of these macromolecules are proteins that exert a complex variety of effects on other proteins, including DBPs, through nonspecific interactions such as hydrogen bonding, ionic interactions, etc. Both the factors are seemingly unfavorable for free diffusion of DBPs inside a crowded nuclear environment.

Recent experiments (26, 27, 28), however, suggest faster diffusion and enhanced enzyme activity of DBPs in the presence of molecular crowders. For example, in vitro studies on the hydrolysis of DNA by endonucleases DNase I and S1 nuclease show substantial increase in a medium crowded by polyethylene glycol (PEG) (29). Facilitated diffusion in crowded medium has been observed experimentally for other systems as well, including translocation of human DNA glycosylases inside highly dense PEG solution (27), optimized regulation kinetics of lac repressor in Escherichia coli (30) and anomalous diffusivity of proteins (31,32). Despite its widespread importance across different types of regulatory processes, how the crowded cellular medium enhances the facilitated diffusion of DBPs remains unclear (33, 34, 35).

Early studies proposed repeated collisions between the molecules in the presence of crowding agents as the molecular basis of tighter binding of protein-DNA complexes (36,37) that can significantly impact the gene expression (38). Further systematic investigation of diffusion in crowded media (22,39) supported the viewpoint and predicted that the role of bulk crowders is to prevent the dissociation of DBPs from the DNA surface and thereby promotes 1D diffusion of the searching protein along the DNA contour over 3D diffusion (40,41). In contrast, previous studies indicate that purely repulsive crowders play a role to decouple the searching protein from the crowding agents during the 1D search regime on a linear DNA stretch (42,43). The observation is along the lines of the Asakura-Oosawa model (44) of crowder action, in which the crowding agents, because of excluded volume interactions with the DNA molecule, result in a preferentially depleted volume around the DNA interface. Because the region is devoid of crowder molecules, the nonspecific rotational and translational diffusion of the searching protein inside this region was found to be independent of the concentration of bulk crowders (42). The protein effectively experiences a constant microviscosity much lower than that of the bulk (45). The model, however, is inconsistent with the protein-based cytoplasmic crowders (46, 47, 48, 49) that exert nonspecific attractive forces on other macromolecules beside excluding the available volume for them. To this end, one should also note the experiments that have reported enhanced facilitated diffusion in the presence of synthetic crowding agents such as PEG. The crowder action is explained exclusively based on the “volume exclusions” by the crowding agents. We emphasize that the “inert” character of PEG molecules is completely misinterpreted in these studies. Indeed, the recent calorimetric experiment indicates that the commonly used synthetic agents such as dextran, glucose, and PEG can significantly contribute to the enthalpic stabilization and the entropic destabilization of proteins (49). The observations and the presence of biomolecules in in vivo conditions that can mediate attractive nonspecific interactions with the DBPs necessitate probing the role of an interacting crowded environment in the facilitated diffusion of DBPs.

Therefore, in this article, we probe the target search dynamics of DBPs in the presence of explicit crowding agents that have an affinity toward other biomolecules. Our aim is to underscore the structural basis of accelerated protein transportation in a nuclear environment by identifying the key molecular determinants associated with it. The study deals with bulk crowders and genomic crowders separately. The latter refers to the DBPs that are already bound to the DNA and spread over the entire genome covering ∼20–50% of it (50). For example, 90% of LacI copies of a cell are hooked to DNA nonspecifically at various sites that are not the cognate site but share a varying degree of sequence similarities with the target DNA site (51). These proteins serve as roadblocks to a searching protein during its 1D diffusion along the DNA. By performing extensive Langevin dynamics simulations, we show that the protein-crowder interactions play a pivotal role in enhancing the facilitated diffusion of DBPs inside a crowded environment. Follow-up structural analysis recognizes efficient target search modes of the searching protein actuated by crowder molecules. The proposed molecular picture is consistent with a cargo transferring mechanism, in which crowder molecules with intermediate nonspecific crowder interactions transport the protein molecule quickly and effectively for faster recognition of the cognate DNA sites. The results are useful to study gene regulation kinetics of transcription factors and detailed models of facilitated diffusion in eukaryotes.

Materials and Methods

Molecular systems

In this article, we used coarse-grained descriptions for protein, DNA, and crowder molecules. Sap-1 (Protein Data Bank, PDB: 1BC8) (52) is selected as a DBP that specifically binds with a nine-basepair (bp) DNA site of sequence ACTTCCGGT. We modeled the protein by replacing each amino acid with a sphere of 2 Å radius placed at the respective C_α positions (see Fig. S1). The protein maintains its folded structure during the simulation with the help of a native topology-based Lennard-Jones potential (53) that promotes only the formation of contacts present in the experimentally determined folded structure of the protein. The DNA molecule is modeled by three beads per nucleotide, placed at the center of phosphate, sugar, and base, respectively. The energy function is adopted from the 3SPN.2C model of DNA developed by Pablo et al. (54). Further details regarding modeling of these two molecules are available in the Supporting Materials and Methods. The DNA model has been successful in predicting structural features of DNA such as major and minor groove geometry as well as its mechanical properties, including persistence length and melting temperature with respect to varying ion compositions (55,56). We model the nonspecific interactions of protein and DNA through short-range repulsive excluded volume interactions and long-range electrostatic interactions captured by Debye-Hückel potential. For electrostatic interactions, we considered unit positive charge on arginine and lysine amino acids and unit negative charge on aspartate and glutamate amino acids. For DNA, a net charge of −0.6 has been placed on every phosphate bead considering the effects of counterion condensation near the DNA surface. The application of Debye-Hückel potential has been widely studied in various nucleic acid and protein biophysics (57,58) despite its limited applicability at low ion concentrations.

Crowder model

The crowding agents are modeled as uncharged spheres that occupy a volume fraction, ϕ = $4N_c$ π $R^3/3L_x{L}_y{L}_z$, where $L_x$, $L_y$, and $L_z$ represent the dimensions of the simulation box. N_c represents the total number of crowder molecules present in the system with a radius R set at 7.8 Å. The value is consistent with the crowder dimension (PEG600) (59) used in the experiments described in (27) that reported enhancement in the facilitated diffusion of glycosylase proteins in the presence of PEG crowding. Our objective is to investigate if the similar kind of crowding environment, but with nonspecific crowder affinity that PEG also features in contradiction to its believed inert character, enhances the facilitated diffusion of DBPs, and if yes, to probe the underlying molecular mechanism. To this end, one should note that this crowder model is not intended to mimic the other features of cytoplasmic crowders such as size heterogeneity that plays crucial roles in regulating various dynamic phenomena (43,60,61); rather, it is to investigate how attractive interactions between searching protein and the crowder molecules affect the diffusion of the former. Although a crowder model that mimics all the features of cytoplasmic crowders, including their compressibility, malleability, size/charge ratio, etc., is always desirable, it may not be straightforward to correlate its action directly with one of its molecular properties.

In this study, we consider the bulk and genomic crowders separately. For bulk crowders, we adopted ϕ = 0.3 for all our simulation studies, which corresponds to the physiological cell crowding. The genomic crowders are modeled by unbiasedly placing the crowder spheres at the major grooves of the DNA at approximately equal distances. Their association with the DNA molecule is maintained through a pseudobonded potential. The crowder molecules are allowed to interact with other crowders, protein, and DNA through a pairwise potential is given by (62) as follows:

$$U_r=\{\begin{array}{ll}{U}_{large}-\frac{U_{large}+\mathrm{\epsilon }}{\delta }\left(r-r_t+\delta \right)& ifr\le r_t\\ -\mathrm{\epsilon }\exp \left[-\left(r-r_t\right)/\lambda \right]& ifr\ge r_t\end{array}$$ (1)

where r_t is the sum of the radii of crowders and interacting beads. The repulsive interaction is modeled by the first part of the equation, whereas the second part is responsible for an attractive interaction. A large finite force, given by $U_{large/\delta }$, maintains the hard-core interaction approximation, and ε (k_BT) gives the attractive interaction strength acting within the characteristic range λ between crowders and other molecules. We set U_large at 40.0 kcal/mol and δ = 1 Å with a characteristic range of 5 Å throughout our work. The attractive interaction is ignored beyond $r-r_t>\lambda$. We note that the model suffers from at least two shortcomings that restrict us to mimic a realistic cellular environment. 1) The interaction strength parameters for all crowding agents are the same. This indicates an environment crowded by only one type of molecule, unlike the cellular milieu. 2) Modeling the crowding agents as a sphere that interacts through an isotropic interaction potential ignores the existence of a more patchy interaction surface, which is abundant in protein molecules. An anisotropic interaction potential (63,64) could be a better approximation for realistic crowding agents. Nonetheless, our model, despite its simplicity, captures the essential features of protein-DNA recognition in a crowded medium.

Simulation protocol

We study the motion of protein, DNA, and crowder molecules through an overdamped Langevin dynamics simulation. The friction coefficient, γ, is set to 0.05 at a temperature T = 300 K and a physiological salt concentration of 120 mM. The simulations are performed by initially placing a 100-basepair (bp) B-DNA in the middle of a 150 × 150 × 410 Å simulation box with periodic boundary condition. The protein is placed far from the DNA molecule, whereas the crowders are distributed randomly inside the simulation box. The initial DNA conformation is generated using w3DNA web server (65) containing Sap-1 binding site at the middle of a random DNA sequence. Upon reaching the target DNA site, the protein specifically binds with the DNA through a soft, attractive Lennard-Jones potential. Further details are given in the Supporting Materials and Methods. All our production runs are 1 × 10⁸ MD (Molecular Dynamics) steps long, during which the role of nonspecific crowder interactions on the DBP dynamics is monitored by varying the attractive interaction strength (ε) of the crowder molecules. The sufficiently long timescale allows studying the multiple association events. This aspect is crucial because recent studies (66,67) suggest that a single timescale in the form of mean first passage time may not be sufficient to represent reaction rates. For each ε, we performed 20 independent runs to investigate the detailed search mechanism with acceptable statistical significance.

We have also performed an all-atom simulation at 300 K to probe interactions between PEG and Sap-1. The simulation was performed using the GROMACS molecular dynamics package with the OPLS force field in the presence of PEG600 crowders. We used a base time step of 2 fs. The neighbor search was performed using the Verlet algorithm and the particle mesh Ewald method that effectively treats the long-range electrostatic interactions. We used the TIP3P water model to perform the simulations.

Estimation of depletion layer dimension and characterizing sliding, hopping, floating, and 3D diffusion dynamics of DBPs inside crowded milieu

We estimated the dimension (width, l_d) of the depleted volume formed because of the presence of crowder molecules around DNA by measuring the average distance between the surfaces of DNA basepairs and their nearest crowder molecules. When the protein approaches the DNA closer than twice the radius of the crowding agents, the depletion regions around protein and DNA molecules merge. The newly formed depletion zone is referred to as the composite depletion zone that features a narrower width because of attractive depletion force. A schematic description of the formation of the composite depletion zone is depicted in Fig. S2.

To identify various search modes adopted by the diffusing protein, we follow the description similar to our previous works (42,43). Briefly, the protein is said to perform sliding if at least 70% of the recognition helix of Sap-1 is within the DNA major groove with an orientation angle of <25°, and the center of mass of the recognition helix lies within 8 Å to the closest DNA basepair in the absence of crowder molecules (see Fig. S3). The associated electrostatic energy $\left(E_{protein-DNA}^{el}\right)$ between protein and DNA ranges from −12 to −8 kcal/mol, indicating the strongest interaction between the two molecules (see Fig. S4). On the contrary, the protein is assumed to be performing 3D diffusion if its recognition helix is more than 25 Å away from the closest DNA basepair. At this distance, protein-DNA electrostatics energy falls to less than 2 kcal/mol. Associated protein dynamics is assumed to be independent of DNA for such low interaction energy. The search mode in the intermediate zone, which is when the recognition helix of Sap-1 is within 8–25 Å from the closest DNA base, is a combination of hopping and “floating” dynamics. These two modes of protein diffusion are inherently different from each other based on the fact that hopping dynamics is driven by the protein-DNA electrostatics, whereas the molecular driving force for the floating dynamics is the nonspecific protein-crowder attraction. Clearly, the statement requires further elaboration. In the hopping model, a protein performs short-range intermittent jumps on the DNA surface and binds to a new section of the nonspecific DNA via multiple rounds of dissociation and reassociation. This is possible if the protein-DNA electrostatics is of moderate strength such that the intermolecular attraction is inadequate to tightly hold the protein on the DNA surface, as it does in sliding, but strong enough to prevent complete dissociation of the protein to the bulk solution. We note when the protein is positioned 8–15 Å away from the closest DNA basepair and does not satisfy any of the sliding criteria, the associated protein-DNA electrostatic energy falls in an intermediate (−8 to −3 kcal/mol) range. It is important to note that the associated protein-crowder attraction under this condition ranges between 0.0 and −0.4 kcal/mol only (see Fig. S5 A), which is not enough to perturb the hopping dynamics of the searching protein. On the contrary, when the protein is 15–25 Å away from the DNA surface and does not satisfy any of the sliding criteria, the protein-DNA electrostatic energy reduces to −3 to −1 kcal/mol. In comparison, the protein-crowder attractive energy rises to −0.01 to −55 kcal/mol for varying ε (see Fig. S5 B), which is strong to pull the protein away from the DNA and hold close to the crowder molecules. The protein is still within the composite depleted volume and moves under the influence of the crowder dynamics. The 1D and 3D diffusion coefficients are estimated from the linear behavior of the mean-square displacement of the protein molecule during 1D (sliding and hopping) and 3D diffusion, respectively.

Results and Discussion

To investigate how molecular crowding enhances DNA target search efficiency of DBPs, we study the diffusion of a transcription factor Sap-1 on a 100-bp linear DNA segment. We performed the experiments separately using explicit random crowder molecules (bulk crowders) and DNA-bound crowders (genomic crowders). For both crowding agents, we systematically vary the strength of the nonspecific protein-crowder interactions and probe the molecular picture of the target search mechanism of DBPs. These experiments help us to identify the molecular determinants responsible for faster search kinetics of DBPs inside crowded milieu.

Bulk crowding modulates environment for 1D and 3D diffusion of DBPs

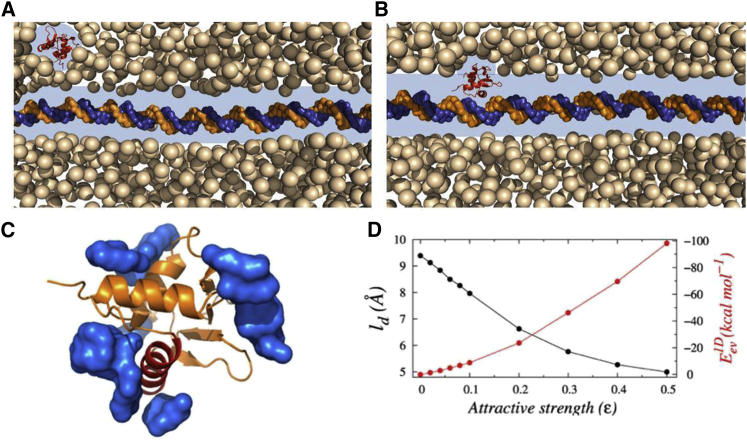
In the presence of bulk crowders, the protein moves mainly in two ways: either it diffuses three dimensionally away from the DNA molecule (see Fig. 1 A) or one dimensionally close to the DNA surface. During 3D diffusion, the protein interacts with the randomly moving crowder molecules, and its overall diffusivity is governed by the concentration, size, shape, and mobility of the crowding agents (43). In comparison, protein diffusion during the 1D search regime was found to be significantly different in the presence of purely repulsive crowders (42,43). This is due to the change in the search environment during 1D diffusion of the protein. Study indicates that when protein approaches the DNA closer than twice the radius of the crowder molecules (see Fig. 1 B), their individual depleted volumes merge because of an entropic force, and the combined volume of the newly formed depletion zone around the protein-DNA complex (composite depletion zone (44)) decreases (see Fig. S2). The microenvironment inside the depletion zone, which is spanned over a few nanometers over the DNA surface, features much lower viscosity in the absence of crowder molecules compared to that of the bulk solution. A similar observation is noted in a study on the cleavage of DNA in crowded solutions that suggests a diffuser experiences a nanoviscosity, much smaller than the macroviscosity of the bulk solution if its radius is smaller than that of the crowding agents (45). Therefore, the protein dynamics, within the depleted region is independent of the bulk crowder concentration (their physiological properties (43)) and follows a 1D random walk along the DNA contour. Presumably, the effect would be different for interacting crowder molecules, for which the enthalpic contribution from crowders needs to be taken into consideration while studying the formation of the depletion zone around the DNA molecule and the protein diffusion inside it. The situation closely resembles the nuclear environment, where proteins and other biomolecules frequently interact among themselves through nonspecific attractive forces. We emphasize that similar nonspecific attractive interactions act for PEG crowders as well, which has been otherwise considered as an inert crowding agent. Indeed, our all-atom MD simulation (see Materials and Methods for details) of Sap-1 with ∼350 mg/mL solution of PEG600 crowders suggests that PEG molecules bind on a specific surface of Sap-1 (Fig. 1 C, blue region) through weak, nonspecific attractive interactions. Our result is in line with a few other studies that have confirmed active interactions of PEG molecules with biological milieu (68,69) and, therefore, implies that the reported enhancement of facilitated diffusion of DBPs (27,29) in the presence of PEG crowders can not be explained exclusively based on volume exclusion. Rather, its nonspecific affinity for other biomolecules should be taken into consideration. Our aim is to understand how such nonspecific crowder interactions affect the microenvironment of a DBP searching for its target DNA site. We investigate this by simulating the protein diffusion on DNA in the presence of crowders, in which nonspecific interaction strength of the crowders $\left(\mathrm{\epsilon }/{\text{k}}_{\text{B}}\text{T}\right)$ is varied gradually from 0 to 0.5. Our result in Fig. 1 D shows its direct impact on the width of the depletion region (l_d), which decreases from ∼9.5 to ∼5.0 Å with the increasing ε. The trend is found to be independent of crowder physiology, as we note a similar relation between l_d and ε in the presence of heterogeneous crowder sizes (see Fig. S6). The range of l_d in Fig. 1 D matches well with the experimentally observed depletion width of PEG600 (27). The decreasing trend in l_d is also accompanied by a simultaneous increase in protein-DNA interactions during the 1D DNA search (increasing $E_{ev}^{1D}$), reflecting the rising protein-crowder cross talk during this search regime.

Figure 1.

A schematic representation of the target search process of DNA-binding proteins (DBPs) inside a crowded medium. (A) The crowding agents form depletion zones (highlighted as the blue region) around the protein and DNA molecules separately when they are far from each other (3D diffusion). (B) When the molecules are in close proximity, the depletion regions merge, and the protein moves along the DNA contour one dimensionally through the composite depletion zone. It should be noted that the width of the depletion region is not to scale. In the absence of a searching protein on the DNA surface, the nearest crowder to the DNA locates approximately its radius distance away. The average of such distances provides the estimation of width of the depletion region, shown in (D). The crowder molecules in the front and back of the DNA are removed intentionally to show the depletion region clearly. (C) During both 3D and 1D diffusion, the crowder molecules interact with the diffuser protein through nonspecific short-range attractive forces, as can be seen from the preferential association of PEG600 crowders (shown in the blue surface) on Sap-1 protein surface in an all-atom simulation. In this context, it is worth mentioning that PEG molecules are often considered as inert crowding agents and their influence is described by volume exclusion only. However, results in (C) suggest the presence of a nonspecific attractive interaction between the protein and PEG molecules, which should be taken into consideration while explaining its action. (D) Variations in width of the depletion region (width, l_d) around the DNA molecule and excluded volume interactions $\left(E_{ev}^{1D}\right)$ between the searching protein and the crowder molecules with the increasing attractive strength of crowders (ε) are shown. To see this figure in color, go online.

Protein diffusivity on DNA inside crowded milieu

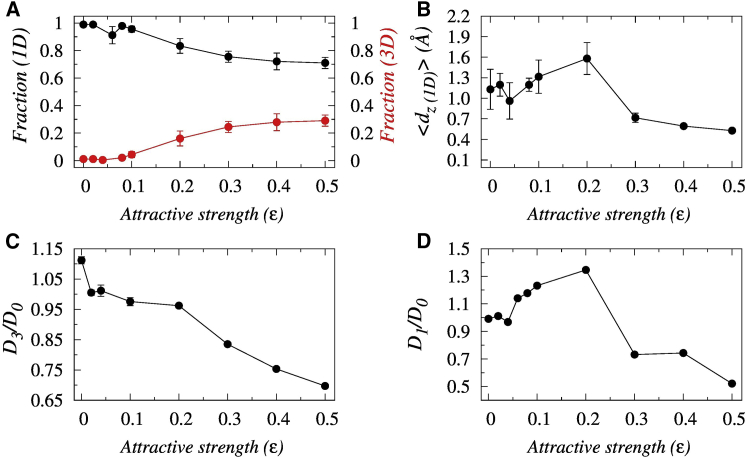
How does the synergistic actions of decreasing depletion width and increasing protein-crowder cross talk with increasing strength of nonspecific protein-crowder interactions, ε, influence the selection of protein search mode? To quantify this, we estimate the propensities of 3D and 1D search modes adopted by the protein to reach the target DNA site and presented them as functions of ε in Fig. 2 A. The results indicate that with increasing ε, the 1D propensity of the searching protein decreases, whereas the 3D diffusion propensity increases. This can be rationalized from the fact that with increasing ε, the strong nonspecific attractive force from the crowder molecules pulls the protein out of the composite depletion volume to the bulk where the protein translocation is 3D diffusion limited. The protein is positioned at least 25 Å away from the DNA surface, where it diffuses independently of the DNA electrostatics. In contrast, a small ε value ensures minimal interference from the crowding agents during the protein diffusion through the depletion zone under the influence of strong DNA electrostatics. This can be seen from the high sliding propensity of the protein at a small ε value, as presented in Fig. S7. The strong DNA electrostatics keeps the protein at close vicinity, and the protein diffuses along with the helical pitch of the DNA slowly to read out the DNA bases. In Fig. 2 B, we present the average displacement (D_z) of the searching protein along the DNA contour during a 1D diffusion event, in which a single event refers to a continuous period in a particular search mode that ends with the change in the search mode of the protein. The result suggests that with increasing strength of nonspecific protein-crowder interactions, diffusion length $\left(d_{z\left(1D\right)}\right)$ exhibits an initial rise up to ε = 0.2 and then a rapid decrease. The trend indicates a trade-off between the electrostatic interactions from the DNA and nonspecific attractions from the crowding agents. For example, a small ε refers to protein dynamics under the influence of DNA electrostatics. The strong nonspecific interactions and the roughness of the interaction landscape with the DNA causes a slow protein diffusion, resulting in relatively shorter diffusion length $\left(d_{z\left(1D\right)}\right)$ per sliding event. Similarly, strong protein-crowder attractions pull the protein away from the DNA surface more frequently and thereby restrict a shorter displacement $\left(d_{z\left(1D\right)}\right)$ in a single sliding event. An intermediate protein-crowder attractive strength partly counters the DNA electrostatics, which promotes a smoother 1D diffusion of the protein. The corresponding $d_{z\left(1D\right)}$ rises accordingly. Similar behavior can be observed for the average duration of hopping events and are shown in Fig. S8. How does such nonmonotonic dependence of $\left(d_{z\left(1D\right)}\right)$ on the ε influence the overall target search efficiency of the protein?

Figure 2.

Effects of nonspecific crowder interactions (ε) on the target search mode of DBPs. (A) The variation in the affinities of 1D and 3D search modes of the searching protein as a function of the ε is shown. (B) Variation in the average Z-displacement traversed by the Sap-1 protein per 1D event on the DNA surface as a function of ε is shown. The impact of nonspecific crowder interactions on the diffusivity of the searching protein is shown. (C) The variation in the relative 3D and (D) 1D diffusion coefficient of Sap-1 as functions of ε is shown. In (D), the associated error bars are smaller than the point size. D₀ represents the diffusion coefficients in the respective modes in the absence of crowder molecules. To see this figure in color, go online.

To probe the issue, we separately estimate the 3D and 1D diffusion coefficients of the protein and present them as a function of nonspecific crowder interactions (ε) with respect to the diffusivity measured in the absence of crowders and presented in Fig. 2, C and D. Our result suggests first a slow and then a sharp decrease in the relative 3D diffusivity of Sap-1 with increasing ε. This is due to the growing stickiness of the crowder molecules with rising ε that holds the protein through strong nonspecific attractive forces and thereby hinders its free 3D diffusion. However, for a purely repulsive crowded environment, the random kicks from the highly mobile crowding agents are actually beneficial to facilitate protein diffusion slightly compared to when protein diffuses in the absence of crowders. This explains why the relative 3D diffusivity of Sap-1 is more than unity for the repulsive (ε = 0) crowders. In contrast, the 1D diffusion coefficient of Sap-1 exhibits a strong nonmonotonic dependence on ε, featuring a maximum at an intermediate ε = 0.2 as shown in Fig. 2 D, suggesting the plausible role of longer 1D events at this ε. The corresponding acceleration in diffusion is 35% greater with respect to that in the absence of crowder molecules. The difference in the relative 3D and 1D diffusivity, however, should not be interpreted as an evidence that absolute 3D diffusivity is smaller than the 1D diffusivity. Rather, our analysis suggests (see Fig. S9) that the 3D diffusivity of the protein is always higher than its 1D diffusivity. This is due to the strong protein-DNA electrostatics that compels the protein to scan the DNA bases precisely at the cost of its speed of diffusion along the DNA contour. The effect might offset the advantage of diffusion through the low viscous environment of depleted volume.

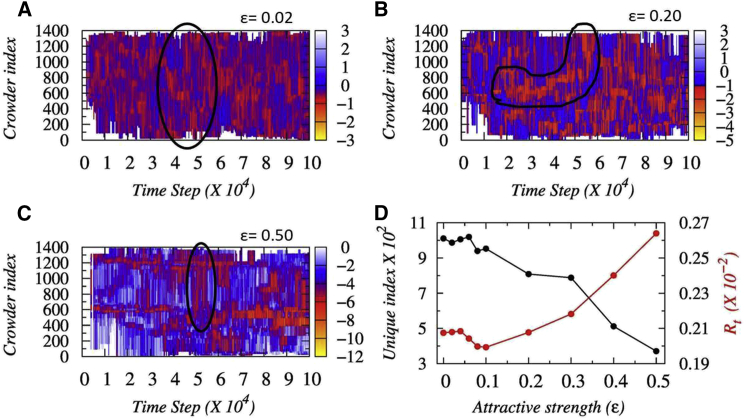
To realize how the protein molecule speeds up the search process during 1D dynamics and the role of crowders in it, we further monitor the movement of the crowder molecules simultaneously with the diffusing protein. In Fig. 3, A–C, we present the time evolution of all crowder molecules at three different strengths of crowder affinities (ε). The fluctuating red lines indicate the indices of the crowder molecules that are interacting attractively with the diffuser protein at any given time. The evolving nature of the lines, therefore, indicates the footstep of the searching proteins monitored through the lens of interacting crowder indices. Our result shows that the unique indices of such interacting crowders decrease with increasing ε as presented in Fig. 3 D. Simultaneously, the transfer rate (R_t) of the protein molecule that depends on the average time spent with the nearest crowder molecule increases. These signify that at low ε, the protein interacts weakly and nonspecifically with the crowding agents and, therefore, can interact with many crowders while diffusing independently. In contrast, at high ε, the strong protein-crowder interactions allow the former to communicate only with the adjacent crowder molecules (the number of unique crowder indices decreases in Fig. 3 D) but only for a short span of time. The strong pull experienced by the protein molecule from the surrounding crowder molecules forces it to shuttle among them, which leads to a high transfer rate, R_t. The protein dynamics at this condition is strongly coupled with the dynamics of neighboring crowder molecules. At intermediate ε, the protein molecule adopts a combination of both independent as well as crowder-regulated search dynamics that promotes longer hopping events and subsequently results in faster protein diffusion. One might expect a similar shuttling mechanism operative for the protein in 3D diffusion as well due to the surrounding crowder molecules and thereby a nonmonotonic trend in the relative 3D diffusivity as was observed by Putzel et al. (62). We note that the effect was reported in the presence of static crowders only, which is unphysical. For a dynamic crowder environment, the rise in relative 3D diffusivity at intermediate ε is not at all substantial (see Fig. S12 of Putzel et al. (62)). To further justify our claim, we estimated the relative 3D diffusivity of Sap-1 in the presence of crowders that have sizes similar to PEG600 (see Table S3) but mass three times more than that of the searching protein. The high mass severely restricts the movement of the crowding agents but does not render them completely static. Our result in Fig. S10 reproduces the similar trend of nonmonotonicity in relative 3D diffusion as reported in Fig. S12 of Putzel et al. (62) in the presence of very slow-moving crowders.

Figure 3.

Protein diffusion through the lens of crowder dynamics. (A–C) Time evolution of indices of crowder molecules that are interacting with the searching protein through the nonspecific crowder interaction strengths ε = 0.02, 0.2, and 0.5, respectively, is shown. The fluctuating lines indicate the indices of the crowder molecules that are interacting with the diffuser protein at any given time. At low ε, the protein interacts with a large number of crowder molecules for a given period of time, whereas on increasing ε, the number of crowders interacting with the protein decreases, as highlighted by the black outlined region. (D) The overall variations in the number of unique interacting crowder molecules and the rate of transfer (R_t) of Sap-1 (red line) from one crowder to another as a function of ε are shown. To see this figure in color, go online.

Crowder-induced search mode for facilitated diffusion

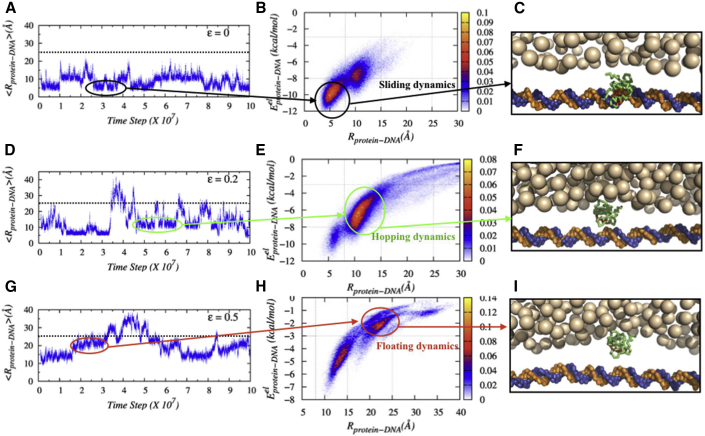
To capture the mechanistic details of the respective search dynamics, we monitor the time evolution of the distance $\left(R_{protein-DNA}\right)$ between the center of recognition helix of Sap-1 and center of the closest DNA basepairs in the presence of crowding agents of varying crowder affinities. The result in Fig. 4 A for ε = 0.0 (purely repulsive crowders) shows that the protein performs primarily 1D diffusion along the DNA. Further inspection suggests that for $R_{protein-DNA}<8$ Å, the protein is under strong influence of DNA electrostatics that orients the former such that the protein reads out the DNA basepair thoroughly in the sliding mode while rotating along the DNA helical pitch with simultaneous advancements along the DNA contour (rotation-coupled sliding; see Fig. S11). In comparison, when the protein is located at 8 Å $<R_{protein-DNA}<15$ Å, it performs small jumps iteratively on the DNA surface (see Video S1). The DNA electrostatic interactions are moderate (−3 to −1 kcal/mol) at this condition that allows the protein to dissociate from the DNA surface for a short time before it comes back again. One should also note here that a comparison of the associated $E_{protein-DNA}^{el}-R_{protein-DNA}$ contour plots in the absence (Fig. S4) and presence of entropic crowders (Fig. 4 B) suggests reduced probability of protein dissociation from the DNA surface (low population of protein for $R_{protein-DNA}>25\mathrm{\AA }$) in the presence of crowding agents, indicating their role in promoting the 1D diffusion of DBPs.

Figure 4.

Structural basis of enhanced facilitated diffusion in the presence of crowding agents. Horizontally, the figures portray 1) the time evolution of distances between the center of recognition helix of Sap-1 and the center of the closest DNA basepair (bp), 2) ${\text{E}}_{protein-DNA}^{el}$-${\text{R}}_{protein-DNA}$ contour plots indicating the differences in various search modes, and 3) their corresponding snapshots showing the protein position during these search modes for nonspecific crowder interaction strengths, ε = 0.0 (A–C), 0.2 (D–F), and 0.5 (G–I), respectively. For simplicity in representation, the crowder molecules in the front and back of the DNA are not shown in the plot. To see this figure in color, go online.

Video S1

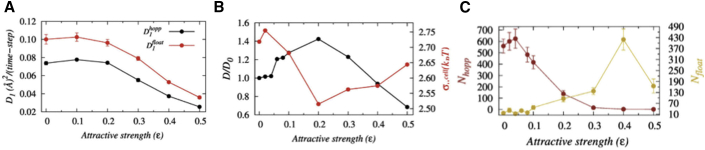
The Protein Performing Hopping Dynamics in a Crowded Milieu

For intermediate to strong nonspecific crowder interaction strengths, the sliding propensity diminishes (see Fig. S7 as well for propensities of various search modes with varying E) because the protein-crowder nonspecific attraction is strong enough to pull the former off the DNA surface and promote hopping and 3D diffusion. Interestingly, here, we find the protein to spend some time in a search mode at 15–25 Å away from the DNA bases. The associated protein-DNA electrostatic energy is inadequate (−3 to −1 kcal/mol; see Fig. 4, E and H) to make the protein hop. How does the protein move then along the DNA? We find that protein-crowder interaction is the driving force. The crowder molecules transport the protein from one crowder to another (see Video S2) and thereby helps the protein to float on the DNA through the crowder-free depletion zone. Estimation of the protein diffusivity (D₁ coefficients; see Fig. 5 A) suggests that such crowder-induced floating dynamics of the protein is ∼36–41% faster compared to that of the hopping dynamics. We also measure the impact of the floating dynamics on the overall search dynamics of the protein and find an ∼39% increment in the overall diffusion coefficient (D₀) at ε = 0.2 in Fig. 5 B compared to the protein diffusion in the absence of crowder molecules. The underlying molecular picture is revealed from the measurement of ruggedness (σ_μ) of associated potential energy landscape following the prescription of Putzel et al. (62) (for more details, see the Supporting Materials and Methods). Fig. 5 B suggests that σ_μ is minimum at moderate nonspecific crowder interactions. This is because of the weak DNA electrostatic field experienced by the searching protein and the absence of crowder molecules inside the depletion zone when the protein is positioned at $R_{protein-DNA}$15–25 Å. A lower or higher ε either favors sliding or 3D diffusion during which the protein experiences highly rugged energy landscape originated from either strong protein-DNA electrostatic interactions or intense nonspecific protein-crowder interactions, respectively. The effective nonspecific crowder interactions toward the diffuser protein can also be increased by simply enhancing the concentration of crowding agents of a given ε. Following the argument, we find in Fig. S12 that protein diffusion first rises with increasing crowder concentration (ϕ), peaks at an intermediate ε value, and then decreases sharply for a fixed ε = 0.2. The result is in line with the experimental observation by Tan et al. (26), who have reported nonmonotonic dependence of gene expression rate on the concentration of PEG 8k crowders, featuring an initial increase, then decrease, and finally a complete halt with rising crowder concentration.

Figure 5.

The impact of crowder-induced floating dynamics of Sap-1 on the overall target search process. (A) a comparison between the efficiencies of hopping and floating dynamics as a function of crowder affinity (ε) is shown. (B) The variation in the overall diffusion coefficient (black line) of the protein (1D + 3D, black lines) normalized by its value in the absence of crowders as a function of ε is shown. The red line suggests the ruggedness of the associated potential energy landscape (red lines) on which the protein diffuses. (C)Variation in the total number of floating (N_float) and hopping (N_hop) events as a function of ε is shown. To see this figure in color, go online.

Video S2

The Protein Performing Floating Dynamics in a Crowded Milieu

To this end, it may be noted that often genomic DNA contains innumerable sites that share high sequence similarities with the target DNA site. These pseudocognate sites work as an antenna to pull down the searching protein onto the DNA surface through attractive interactions. Thus, the stability of the quasi-specific protein-DNA complex at these sites lowers the search speed of the protein. This opposing behavior, known as the “speed-stability” paradox (5,70,71), is a critical factor that governs the protein-DNA interactions. One way the DBPs solve the puzzle is through a frequent conformational transition between nonspecific and specific search modes. Because the protein in nonspecific search mode is not in a position to establish any specific contacts with the DNA bases, the slow down caused by the pseudocognate site does not become functional. On the other hand, frequent conversion to the specific search mode ensures the formation of a specific protein-DNA complex when the protein arrives at its target DNA site. In this study, we find that the presence of crowders regulates the transition from nonspecific to specific search mode. In Fig. S13, we measure the average rate with which the protein switches from the nonspecific search mode to the specific recognition mode (k_a) and the average rate with which the protein orients itself to form the specific protein-DNA complex by establishing all the specific contacts between the protein recognition helix and DNA target site (k_o) as functions of ε. Our results suggest an enhancement in both the rates at intermediate ε, which implies that the presence of crowders with moderate affinity favors the transition of the protein from the search to recognition mode. In addition to this, it is also tempting to speculate that the proposed floating dynamics induced by the bulk crowder molecules with moderate nonspecific crowder interactions could be a way to bypass the antenna effect to expedite the search process. In other words, the proteins and other biomolecules present in the nuclear environment that can moderately interact nonspecifically with the searching DBPs may help the latter in bypassing the pseudocognate sites. We, however, emphasize that the floating dynamics alone cannot assure the fastest target search kinetics; rather, it requires an optimal balance between both the hopping and the floating dynamics. Our analysis at ε = 0.2 suggests the balance is achieved for when the number of hopping (N_hop) events is ∼1.5 times to that of the floating (N_float) events (see Fig. 5 C).

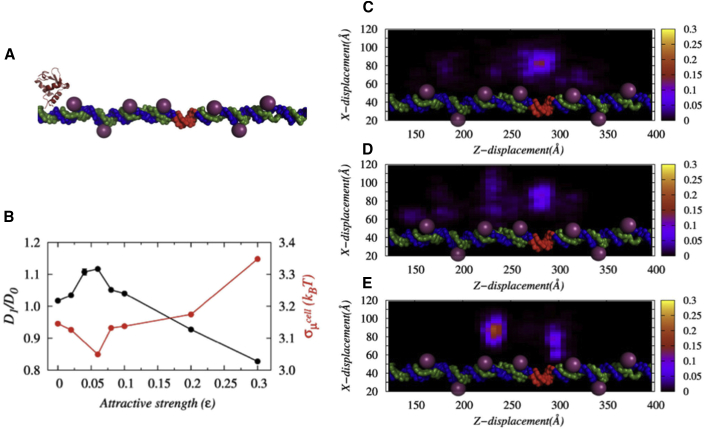
Facilitated diffusion in the presence of genomic crowders

Having seen the role of nonspecific crowder interactions in accelerating the facilitated diffusion of DBPs, we now turn to investigate the influence of interacting genomic crowders that are abundant in nature (∼50% of the DNA surface is occupied by a vast majority of different kinds of proteins) (50). It has been noted that such genomic crowders often act as roadblocks to nearby searching proteins and hinder their diffusion (72,73). In contrast, few other studies have reported marginal to a significant rise in diffusion efficiency of DBPs in the presence of genomic crowders (35,74). Clearly, the prevailing ambiguity requires deeper insights, particularly when the crowders may nonspecifically interact with the diffuser protein. Does the interaction retard the diffusion of nearby proteins by halting them as many pseudocognate sites do? We investigated the issue by estimating the 1D diffusion coefficient of the protein as a function of nonspecific crowder interactions (ε) of the DNA-bound crowders. Fig. 6 A presents a schematic representation of the system, and Fig. 6 B suggests a nonmonotonic dependence of the 1D diffusion coefficient on nonspecific crowder interactions, ε, with a maximum observed at ε = 0.06. The associated D1 enhances by ∼12% compared to when there are no genomic crowders present. The measurement of the potential energy ruggedness confirms the least ruggedness at ε = 0.06 on which the protein can quickly diffuse along the DNA contour. The same can be realized from the contour plots as well, presented in Fig. 6, C–E. The spots on the plot show the position of the protein during our simulations. Interestingly, the protein positions in all these plots are not exactly aligned with the position of genomic crowders; rather, they are more probable in between two consecutive genomic crowders. How is it connected with protein diffusion?

Figure 6.

The role of genomic crowders on the target search process of DBPs. (A) A schematic representation of the target search process of Sap-1 (in orange) in the presence of DBPs that are already bound to the DNA (presented through spheres) is shown. (B) The variation in the 1D diffusion coefficient (in black lines) of the protein normalized by the diffusion coefficient in the absence of crowder molecules (D₀) and the variation in the ruggedness of the potential energy landscape (in red lines) as a function of ε are shown. (C–E) Contour plots show the probability of protein positions on the x-z plane for nonspecific crowder interaction strengths ε = 0, ε = 0.06, and ε = 0.5, respectively. The brighter the spot, the higher the probability is of finding the protein at that position. To see this figure in color, go online.

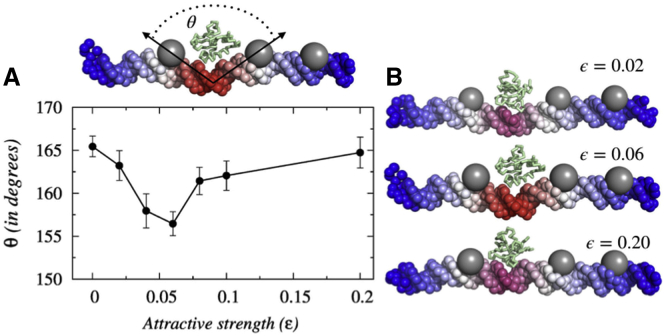
A detailed structural analysis suggests that nonspecific crowder interactions allow adjacent or spatially close genomic crowders to interact with the nearby searching protein simultaneously, through the formation of a transient bridged complex (see Fig. 7 B). For genomic crowders on linear DNA, such interactions require deformation in the DNA conformation to bring the interacting crowders spatially close. In Fig. 7 A, we measure the DNA deformation through the angle (θ) formed between two adjacent genomic crowders and present as a function of nonspecific protein-crowder interaction strength. The results imply that for moderate ε, the kink angle θ is minimum to promote the jumping of the protein from one crowder to another genomic crowder through the local deformation in DNA conformation and subsequent formation of a transient bridged complex. The formation of the transient bridged complex can be realized also from the measurement of search efficiency of the protein along the DNA contour. In Fig. S14, we present an estimation of the average time spent by the protein molecule on each DNA base in the presence and absence of genomic crowders. The genomic crowder positions (shown by black arrows) clearly indicate that the protein does not scan the DNA length with equal efficiency. It spends a significant amount of time at the middle of two genomic crowders, which supports the formation of the bridged complex. Because of the formation of the bridged complex, the protein quickly rolls over the other DNA sites compared to when genomic crowders are not present. The overall speedup in the search process depends on the stability of the bridged complex. For purely repulsive crowders, the formation of such a bridged complex is not permitted, whereas the presence of strongly attractive genomic crowders (high ε) hold the searching protein tightly and thereby are unlikely to share it with other crowders for the formation of a bridged complex. The trend is reflected in the reduction in associated deformation in DNA (θ). The search process may also get affected by the positions, density, mobility, and size of the genomic crowders (72,73,75). For example, upon lowering the crowder density on DNA (by placing crowders on every alternative major groove), we find a reduction in search efficiency (∼3%) compared to our previous arrangement of genomic crowders placed on every DNA major grooves. For specific DBPs, the search process can still be facilitated (76) because of the formation of DNA loops and coils that are known to enhance protein translocation on DNA (77,78). However, the nonmonotonic dependence of 1D diffusion coefficient on ε is general and remains the same that features a peak in D₁ (see Fig. S15) corresponding to the maximal DNA deformation (see Fig. S16) at ε = 0.15.

Figure 7.

Crowder-induced kinks in the DNA conformation and subsequent formation of a transient bridged complex. (A) Variation in the degree of the DNA deformation (θ) as a function of ε is shown. The deformation originates when Sap-1 interacts with adjacent genomic crowders attractively. The crowder molecules tend to approach closer to the interacting protein and thereby cause local kinks in the DNA structure. (B) A schematic representation of the kink formed in the DNA structure for three different nonspecific crowder interaction strengths ε = 0.02, ε = 0.06, and ε = 0.2 is shown. The increasing degree of bending is represented by the change in color from blue to red. To see this figure in color, go online.

Conclusions

Through extensive molecular simulations of a coarse-grained model, we investigated the molecular mechanism of how the facilitated diffusion of DBPs enhances in the presence of crowded environment, where the crowding agents are capable of interacting with other biomolecules through attractive forces as in vivo crowders do. Despite the similarity, it is noteworthy to mention that modeling a realistic crowded environment needs to take several other factors into account, such as heterogeneous crowder sizes and masses, anisotropy in their interactions with other biomolecules, and positional preferences around the DNA according to crowder physiology. Nonetheless, our model is successful in capturing the essential features of protein-DNA recognition in crowded environment along with the formation of depletion zone around a DNA molecule with a dimension comparable to that observed in the presence of a synthetic crowder (PEG600). Any change in the crowder interaction strength is found to have a direct impact on the dimension of the depletion zone. The analysis, therefore, finds the crowder interaction strength as a key component in investigating the DNA target search dynamics of DBPs in a crowded medium. For example, we observe that the crowder molecules with moderate interaction strength expedite the search kinetics of DBPs maximally compared to when no crowder molecules are present. The counterintuitive result is understood from the structural analysis of simulation trajectories that identifies kinetically efficient alternative search modes of DBPs induced by the crowding agents. For bulk crowders, the alternative search mode resembles a protein floating one dimensionally along the DNA contour. Unlike the hopping dynamics during which protein iteratively performs small jumps near the DNA surface under the influence of the electrostatic field of the latter, the protein in the floating dynamics diffuses significantly away from the DNA surface, where it feels the DNA electrostatic field only marginally. The trade-off between weak DNA electrostatics and moderate crowder interaction presents a potential energy landscape with minimal ruggedness, suitable for maximal gain in search kinetics. On a similar note, the genomic crowders with moderate ε enhance the facilitated diffusion of a nearby interacting protein by transporting it from one to another adjacent crowder through the formation of a transient bridged complex between protein and adjacent genomic crowders. The DNA conformation subsequently adopts a locally kinked conformation to facilitate the process and helps the protein to bypass scanning the intermediate DNA bases to achieve faster kinetics. Both the proposed search modes are viable to only intermediate nonspecific crowder interactions. A stronger or weaker crowder interaction either holds back the protein for long and retards the search process or only marginally influences the protein dynamics. The emerged molecular picture is also consistent with the nonmonotonic dependence of the target search efficiency of DBPs on bulk crowder density observed by Tan et al. (26) and is useful to study gene regulation kinetics of transcription factors and facilitated diffusion in a crowded cellular environment.

Author Contributions

A.B. designed the research. P.D. and A.B. performed the research. P.D. and A.B. analyzed the data. P.D. and A.B. wrote the article.

Editor: Anatoly Kolomeisky.