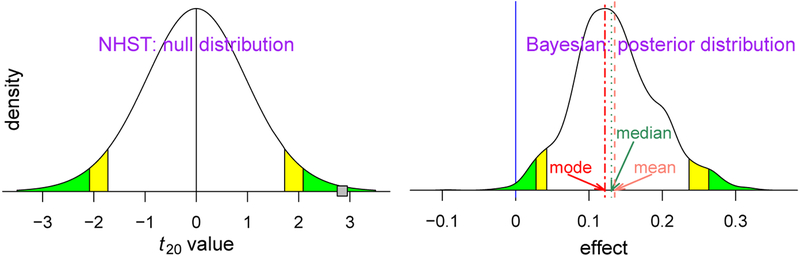
Fig. 5.

Different probability definition and focus between the conventional and Bayesian frameworks. Statistical inferences under NHST usually pivot around the “weirdness indicator” of the p-value (left curve): green (or yellow) tails symbolize a two-sided significance level of 0.05 (or 0.1). If the data renders a t₂₀ value of 2.85 (small gray square), reaching the comfort zone (green or yellow area) with a two-tailed p-value of 0.01 (the probability of obtaining such data with a t₂₀ value at least as extreme if the effect were truly zero), one may declare to have strong evidence for the effect with an FPR threshold of 0.05 under the NHST framework. In contrast, inferences under the Bayesian framework directly address the research interest (right curve): what is the probability of the effect magnitude being greater than 0 with the data at hand (greater than 0.99 in this case)? There are different ways to provide a point estimate of centrality from the posterior distribution such as mean, median and mode (or maximum a posteriori probability (MAP)) under the Bayesian framework, while such point estimates are usually the same due to symmetry under the theoretical distribution of NHST. However, Bayesian inferences tend to emphasize more the uncertainty of an effect, not its point estimate. The green and yellow tails of the posterior density mark the extent of statistical evidence associated with the two specific (two-sided 95% and 90%) uncertainty intervals, and the dotted dark green line shows the median or 50% quantile of the posterior density. Notice 1) the x-axis is different between the two densities (standardized value for NHST and effect in physical dimension for the Bayesian paradigm), 2) P(data | zero effect) under NHST is conceptually and numerically most of the time not the same as 1–P(effect > or < 0 | data) under the Bayesian framework, 3) the null distribution under NHST has a smooth and regular shape due to the assumption of a standard curve in the model as a prior while the irregular posterior distribution is formulated through random samples through Markov chain Monte Carlo simulations under the Bayesian framework, and 4) compared to the conventional confidence interval that is flat and inconvenient to interpret, the posterior density provides much richer information such as spread, shape and skewness.