Fig. 2. A time to threshold method for conjugation quantification.

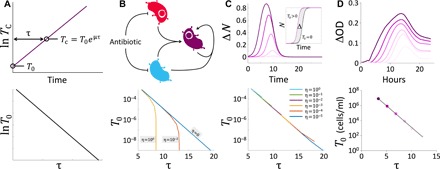
(A) The principle of time to threshold quantification. Consider the exponential growth of the transconjugant from an initial density T₀ (top panel). The time (τ) required for the population to reach a set threshold (T_C) is uniquely determined by T₀ and the specific growth rate (μ). This defines a log-linear relationship between T₀ and τ: lnT₀ = ln T_C − μτ (bottom panel). (B) Quantification of T₀ is complicated by the presence of donor and recipient cells. Top panel: Although strong antibiotic selection is applied against donor and recipient cells during transconjugant outgrowth, death is not instantaneous (i.e., conjugation may still occur). Bottom panel: Modeling reveals conjugation of variable efficiency (η) during outgrowth causes a deviation from the log-linear relationship. This effect is amplified with smaller T₀, where transconjugants produced from outgrowth conjugation—not outgrowth alone—may comprise a sizeable proportion of the total transconjugant population. (C) Correcting for outgrowth conjugation. Top panel: The growth contribution from the transconjugant alone can be approximated by the difference (ΔN) between the growth curves originating from the conjugation mixture (T₀ > 0) and conjugation control (T₀ = 0). Darker curves represent higher T₀. Bottom panel: Using ΔN, the log-linear relationship between T₀ and τ is maintained even in the presence of conjugation during outgrowth. (D) Applying the time to threshold method to experimental data. T₀, spanning six orders of magnitude, maintains a strong correlation (R² > 0.99) with τ from a ΔOD threshold. Darker curves represent higher T₀.