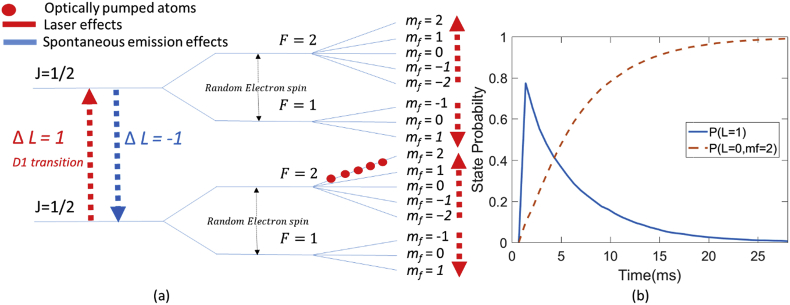
Fig. 3.

Optical pumping of ⁸⁷Rb. In (a) the laser will always provide an increment in $m_f$ and, if possible, a D1 transition (from L = 0 to L = 1). This transition however will only be possible if $m_f$ < 2 (as the maximal possible value for $m_f$in the L = 1 state is 2). If the sample is in the L = 1 state it may spontaneously emit light (at 795 nm) reversing the D1 transition (but not necessarily the change in $m_f$ as the emitted light is equally likely to emit light with$m_f=\mathrm{0,1},-1$ ). The result is that atoms begin to accumulate in the L = 0, F = 2, $m_f=2$ state. At this point (as there is no $m_f$ =3 state in L = 1) the laser light can no longer drive a D1 transition and passes through the vapour without attenuation. This process is schematised over time in (b) where initially the probability of an atom in the L = 1 state (due to D1 transition) or the L = 0, $m_f$ =2 state is low. The action of the laser initially increases the probability of the L = 1 state being occupied (due to D1 transitions) but also increases the probability of the L = 0, $m_f$ =2 state occurring due to optical pumping. As atoms become trapped in the L = 0, $m_f$ =2 state the probability of D1 transitions drops towards 0 thus rendering the vapour transparent (Figure b is only intended for illustrative purposes and is not intended to be realistic. It was simulated by measuring the frequency of atoms (N = 10000) in a given state following the application of circularly polarised photons to atoms uniformly distributed throughout the ground state Zeeman sub-levels. On some iterations the atoms were allowed to spontaneously emit light with equal probability of $m_f=0,1,-1.$Note this does not include effects of spin exchange which are to be covered later).