Figure 1.
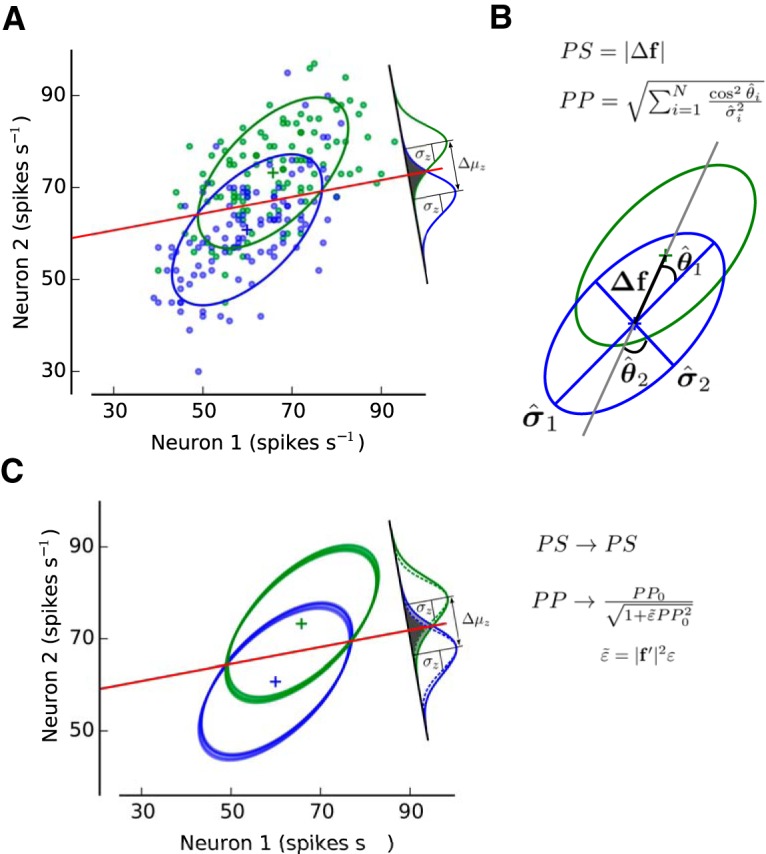
The information encoded by a neuronal ensemble is fully characterized by population signal (PS) and projected precision (PP). A, The trial-by-trial joint activity of a network consisting of N neurons can be characterized by an ellipsoid embedded in an N-dimensional space (a representative population of two MT neurons from Monkey 4 is shown here; see Fig. 2; see Materials and Methods). The covariance matrix and mean activity of the population determine the shape and location of the ellipsoids corresponding to stimulus 1 (s1; green) and stimulus 2 (s2; blue). The linear classifier is characterized by a linear boundary that separates the two clouds of points as well as possible (red line). The difference in mean value for the decision variable z and its SD are represented by Δμz and σz, respectively (signal-to-noise ratio of d′). B, Graphical depiction of PS and PP. PS is defined as the norm of the tuning vector, Δf, which corresponds to the distance between the mean responses associated with s1 and with s2 (distance between the centers of the green and blue ellipsoids). PP is calculated from the angles (θ̂i) between each eigenvector of the covariance matrix and the tuning vector (Δf) (orientation of each axis of the ellipsoid with respect to Δf) as well as from their eigenvalues (σ̂i2; length of each axis). Greater information is encoded when the longest axis of the ellipsoid becomes orthogonal to the direction of Δf. Mean pairwise correlations (MPC) is defined as the mean across all neuronal pairs of the trial-by-trial covariability (Pearson correlation) for a given set of trials. Global activity (GA) is defined as the mean activity across trials neurons and neurons for a set of trials. C, When information-limiting correlations are added into the system, the amount of encoded information is harmed due to a reduction of PP. Because PS accounts for the contribution of the population tuning on encoded information, it is not affected by the presence of information-limiting correlations. The magnitude of the reduction in PP will depend on the strength of information-limiting correlations (ε), the sensitivity of the population tuning to stimulus changes (|f′|2), and PP without information-limiting correlations (PP0) (see Materials and Methods). See also Figure 1-1, Figure 1-2, and Figure 1-3.
