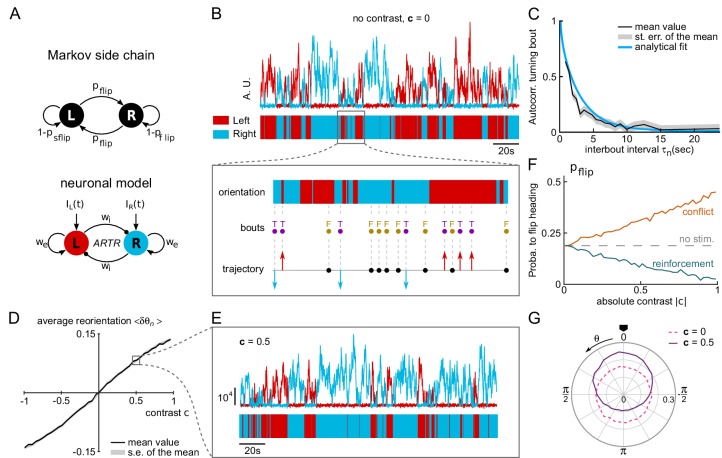
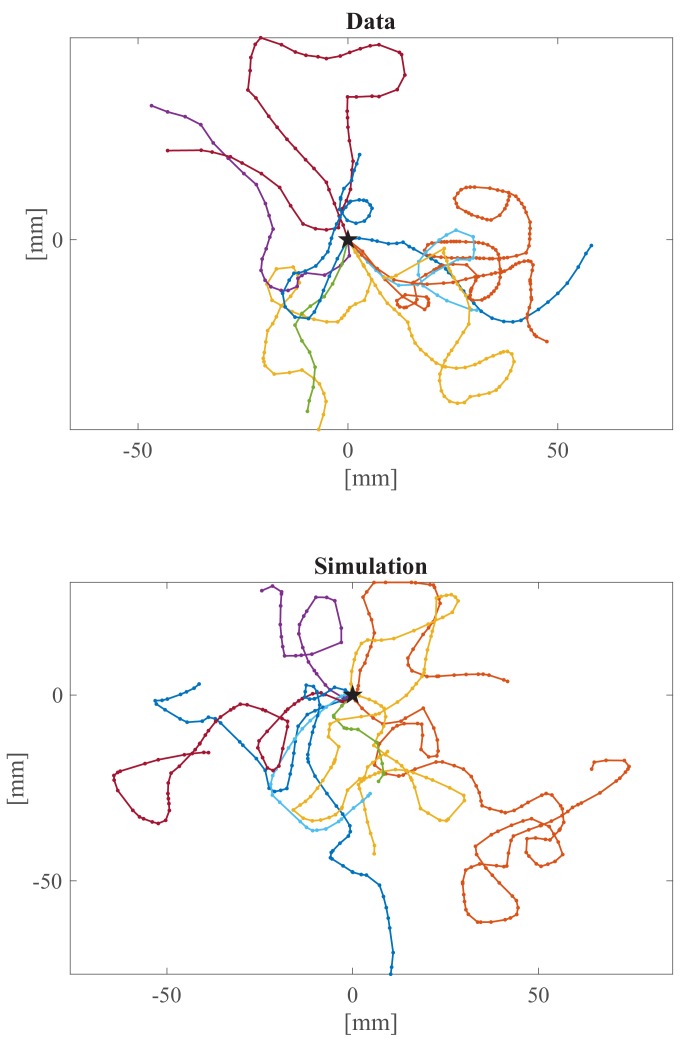
Figure 5. A neuronal model of turning bout selection captures spontaneous and contrast-driven navigation.

(A) Scheme of the Markov-chain model of the orientation selection, and corresponding neuronal model of the ARTR. The latter consists of two units whose relative activation controls the orientation of bouts. Persistent and self-alternating dynamics result from the recurrent excitation ($w_E$) and reciprocal inhibition ($w_I$) between each unit. They further receive input currents proportional to the illumination of the ipsilateral eye. (B) Top: example traces of the simulated activity of the left (red) and right (blue) modules in the absence visual stimulation (AU : arbitrary units). These continuous dynamics control the alternation between right and left orientational states. Close-up: forward and turning bouts are triggered independently with a statistics drawn from the behavioral recordings. The orientational state governs the orientation of the turning bouts. (C) Orientation correlation of turning bouts (thresholded at 0.22 rad) as a function of the inter-bout interval ${\tau }_n$. Result from the neuronal model is in blue, experimental data are in black. (D) Mean reorientation $⟨\delta \theta ⟩$ as a function of the contrast $c$. (E) Example traces of the simulated activity for a constant contrast $c=0.5$. (F) Probability of flipping orientation as a function of the imposed contrast $c$ in situations of conflict or reinforcement (neuronal model). (G) Probability distribution function of $\theta$ for 10 simulated phototactic trajectories with a linear dependence of average reorientation on contrast. Each trajectory lasted 50,000 s. The dotted line is the orientational distribution in the absence of visual stimulation.

Figure 5—figure supplement 1. Comparison of experimental and simulated trajectories.

Examples of experimental and simulated (neuronal model) trajectories. The black star indicates the initial position of each trajectory. Each dot corresponds to one swim bout.

Figure 5—figure supplement 2. Simulated trajectories with different inter-bout intervals ${\tau }_n$.

Examples of simulated trajectories with different inter-bout intervals ${\tau }_n=1$ displaying different fractal dimensions $H$. Units : mm. (A) ${\tau }_n=1$ s, $H=1.5$. (B) ${\tau }_n=5$ s, $H=1.3$ (C) ${\tau }_n=10$ s, $H=1.2$. Red segments represent the onset of a sequence.