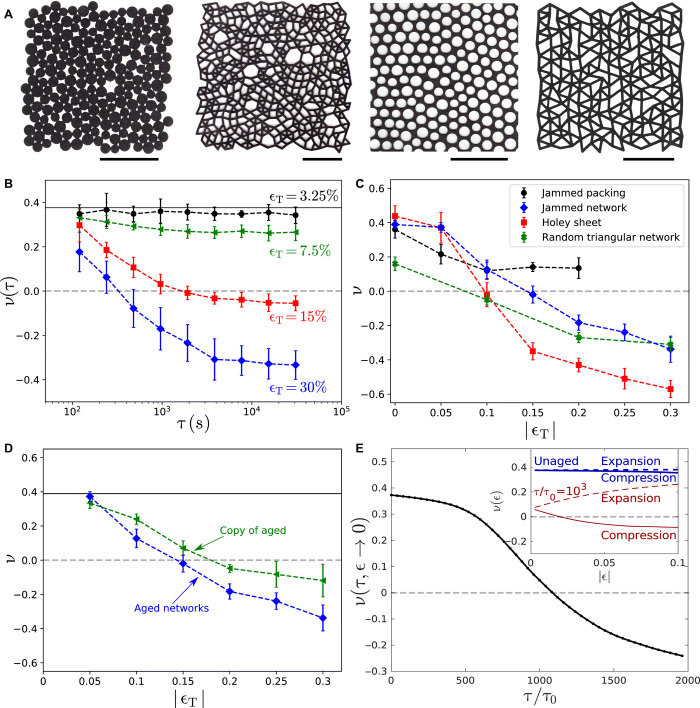
Fig. 1. Change in Poisson’s ratio, ν, by aging.

(A) Sample systems of each kind that were trained. Left to right: a jammed packing of discs, a network based on jamming, a disordered holey sheet, and a random network based on triangular lattice. Scale bars, 50 mm. (B) Effect of aging as a function of time (seconds). When foam networks are aged under constant strain, the Poisson’s ratio drops until it saturates to a final value. Different curves represent different aging strains. The horizontal line at 0.38 shows the initial ν of the networks. (C) Four different systems: jammed packings (black circles), jammed networks (blue diamonds), holey sheets (red squares), and random triangular networks (green crosses) show a drop in ν when aged under uniform compression. (D) Role of geometry: Networks prepared by aging under different strains (blue diamonds) compared to unaged networks cut out to have the same geometry (green squares). The deviation suggests that both geometry and the material properties change during aging. (E) Results from numerical simulation of a system aged at 2.5% compressive strain. The Poisson’s ratio within linear response decreases as a function of time. Inset: The Poisson’s ratio in the nonlinear regime as a function of the measuring strain for unaged networks and networks aged at τ/τ₀ = 10³. Note that the system is not auxetic within linear response but auxetic when compressed to larger strains.