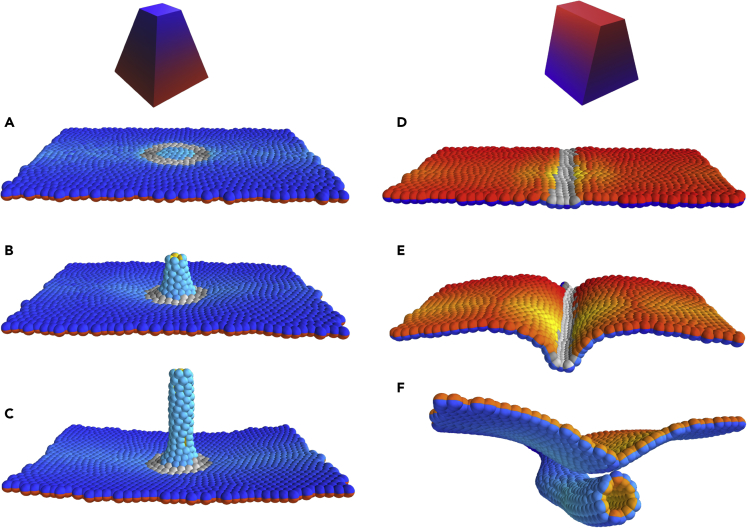
Figure 2.

Isotropic and Anisotropic Wedging Drive Budding and Wrapping, Respectively

Wedging cells are labeled in gray, with a shading that indicates the PCP direction.

(A–C) Time evolution of budding simulation (similar to Drosophila salivary glands). Here, gray cells constrict basally and all cells on and inside the ring intercalate radially. The couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.5,0.4,0.1\right)$, the degree of wedging is $\left|\alpha \right|=0.5$, and the annulus within which wedging occurs is given by the radii $r_0=5$ and $r_1=15$. See section Modeling budding from a plane for details, as well as Figure S5. Total number of time steps was $6.25\times {10}^4$ at $\text{d}t=0.2$. Snapshots correspond to times 5, 800, and $1.25\times {10}^4$. The width of the Gaussian noise was $\sigma =0.05$. See also Figures S1, S7, and S8, Video S2.

(D–F) Time evolution of wrapping simulation (similar to neurulation). Here, gray cells representing neuroepithelium constrict apically and constriction is anisotropic, follows the direction of PCP (Eq 3). Cells proliferate only at the gray/colored boundary (with 7-h doubling time), mimicking differential proliferation at the neuroepithelium/ectoderm boundary. The couplings are $\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\left(0.6,0.4,0\right)$, the degree of wedging is $\left|\alpha \right|=0.5$. See section Modeling neurulation/wrapping for details, as well as Figure S4.

Total number of time steps was $3.9\times {10}^4$ at $\text{d}t=0.1$, and snapshots were taken at times 5, 900, and $3.9\times {10}^3$. The cell cycle length in simulation time units is 600. This simulation was run without added Gaussian noise, but noise is supplied by proliferation, which is implemented as a Poisson process. See also Videos S4 and S5.