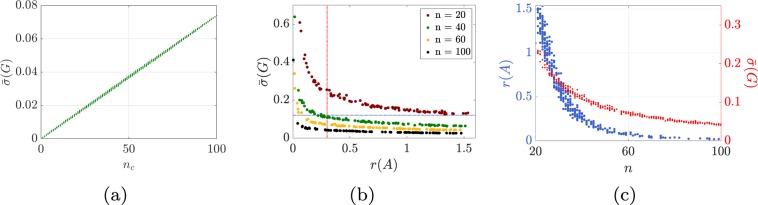
Figure 3.

This figure illustrates the tradeoff between fragility and responsiveness described in (4) in synthetic networks with bounded weighted in- and out-degree. Panel (a) shows the linear relationship between $\overline{\sigma }(G)$ and $n_c$, when the matrix $A$ is fixed (hence, also $n$ and $r(A)$ remain fixed). Specifically, we let $n=100$, consider a randomly generated regular graph with in- and out-degrees equal to $20$, and construct the network matrix $A$ by randomly associating a weight between 0 and 1 with each edge. Then, we stabilize the matrix $A$ by adding suitable negative constants to the diagonal weights. For each $n_c=1,\dots ,n$, we select 50 random choices of $n_c$ control nodes. Each plotted point represents a single realization of $\overline{\sigma }(G)$. Panels (b,c) describe the tradeoff expressed by (4) when $n_c$ is fixed and equal to 20. In panel (b), for $n\in \{20,40,60,100\}$, we randonly construct 100 network matrices with edge weights between 0 and 1 and in- and out-degrees equal to 6 (each matrix is stabilized by adding negative constants to the diagonal weights). Finally, panel (c) shows two cases where either $r(A)$ or $\overline{\sigma }(G)$ remains constant (red dots in (c) and red dashed line in (b), and blue dots in (c) and blue dashed line in (b)), as n increases from 20 to 100.