Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2020 Jan 31;8:34. doi: 10.3389/fbioe.2020.00034

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

Copyright © 2020 Koutrouli, Karatzas, Paez-Espino and Pavlopoulos.

This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

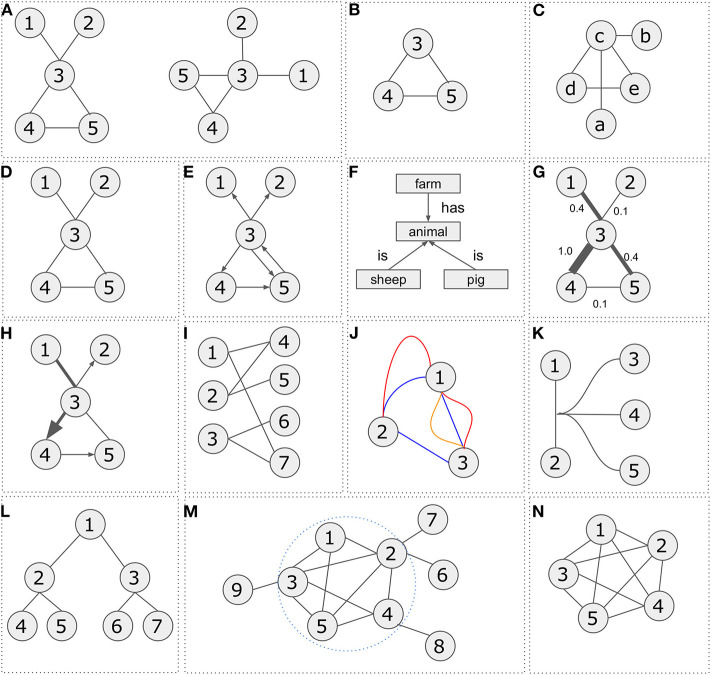
PMC Copyright notice

Network representations and types. (A) Two graphical representations of a graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5} and edge set E = {{1, 3}, {2, 3}, {3, 4}, {3, 5}, {4, 5}}. (B) Representation of subgraph G′ = (V′, E′) with vertex set V = {3, 4, 5} and edge set E = {{3, 4}, {3, 5}, {4, 5}}. (C) Graph G″ = (V″, E″) is isomorphic to graph G = (V, E) with vertex set V = {a, b, c, d, e} and edge set E = {{a, c}, {b, c}, {c, d}, {c, e}, {d, e}}. (D) Undirected graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5} and edge set E = {{1, 3}, {2, 3}, {3, 4}, {3, 5}, {4, 5}}. (E) Directed graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5} and edge set E = {{3, 1}, {3, 2}, {3, 4}, {4, 5}, {3, 5}, {5, 3}}. (F) Semantic graph. (G) Weighted graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5} and edge set E = {{3, 1, 0.4}, {3, 2, 0.1}, {3, 4, 1.0}, {4, 5, 0.1}, {3, 5, 0.4}}. (H) Mixed graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5} and edge set E = {{1, 3}, {3, 2}, {3, 4}, {5, 3}, {4, 5}}. (I) Bipartite graph with vertex set V′ = {1, 2, 3}, V″ = {4, 5, 6, 7} and edge set E = {{1, 4}, {1, 7}, {2, 4}, {2, 5}, {3, 6}, {3, 7}}. (J) Multi-edge graph G = (V, E) with vertex set V = {1, 2, 3} and three different types of edge sets E′ = {{1, 2}, {2, 3}, {3, 1}}, E″ = {{1, 2}, {1, 3}}, E^‴ = {{1, 3}}. (K) Hypergraph G = (V, E) with vertex set V = {1, 2, 3, 4, 5} and an edge connecting multiple nodes E = {{1, 2, 3, 4, 5}}. (L) A tree graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5, 6, 7} and edge set E = {{1, 2}, {2, 4}, {2, 5}, {1, 3}, {3, 6}, {3, 7}}. (M) A graph G = (V, E) with vertex set V = {1, 2, 3, 4, 5, 6, 7, 8, 9} and edge set E = {{1, 2}, {1, 3}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {2, 7}, {3, 4}, {3, 5}, {3, 9}, {4, 5}, {4, 8}}. A cluster consisting of nodes V = {1, 2, 3, 4, 5} and edges E = {{1, 2}, {1, 3}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}}. (N) A five-node clique on the right. Any node is connected with any other node.