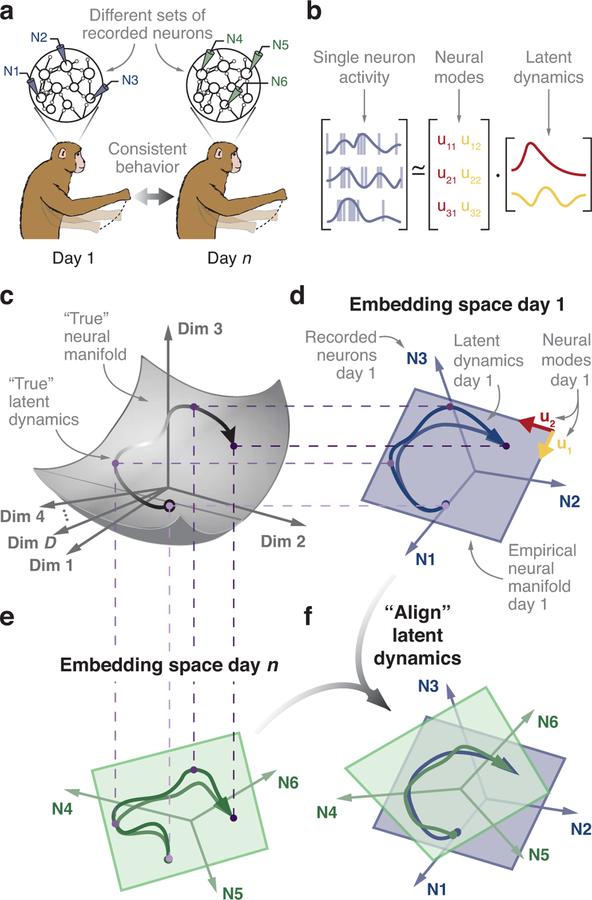
Figure 1.

Hypothesis. (a) Subjects perform the same behavior over days, yet in typical experimental setups the same neurons cannot be recorded over this period. (b) In our model, the single neuron activity results from a weighted combination of the latent dynamics of the neural modes. (c) The latent dynamics (black line, arrow indicates passage of time) underlying a behavior are mostly confined to a “true” manifold (gray surface) within the full D-dimensional neural space that involves all neurons modulated by the task. (d) The activity of the recorded neurons (N1, N2, N3 in this example) is represented in an empirical neural space in which each axis corresponds to the activity of one recorded neuron. During behavior, the recorded population activity describes a trajectory (blue trace). During movement, such trajectories are typically confined to a low-dimensional neural manifold (blue plane). The projections of the population activity onto the two axes that define the neural manifold in this example are the empirical latent dynamics. (e) Latent dynamics during the same behavior but on a different day, with a different set of recorded neurons. We hypothesize that the true latent dynamics for a given behavior will be stable during repeated execution across days, even when the empirical manifold to which the latent dynamics are confined is embedded in a different empirical neural space. (f) We predict that, in the face of neural turnover, the stable latent dynamics can be recovered by linear alignment.