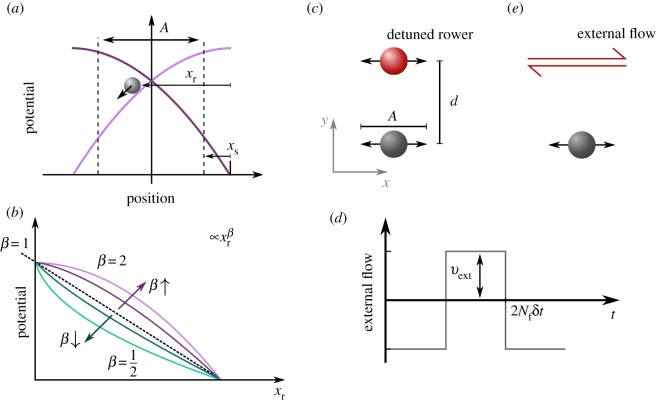
Figure 1.

The model of ‘rower’ phase oscillators is used to compare the mutual synchronization facilitated by viscous forces, with entrainment to an external flow. (a) Each oscillator is driven by a repulsive trap, which is updated geometrically. When the rower passes a switch point A + x_s the trap is reflected and drives the rower in the opposite direction. This creates oscillations with amplitude A, and free period and phase. For simplicity, distances are measured relative to the vertex, with the relative position of the rower within the trap x_r. The switch point is controlled through parameter x_s, which is also measured relative to the trap vertex. (b) The driving potentials take the form of power laws, which results in position-dependent force $F=k\beta x_{\mathrm{r}}^{\beta -1}$ with k the trap strength. When varying β, k is also updated to maintain a constant non-detuned frequency f₀. The curvature of the potential is known to relate to the synchronization strength, with increasing |β − 1| also increasing the level of noise at which rowers maintain synchrony [16]. Here, entrainment and synchronization are compared by considering the detuning range in which phase-locking occurs. (c) Two rowers have their traps separated by a distance d, with one rower detuned and marked in red. This rower has a frequency f_d, while the grey has frequency f₀. The separation is perpendicular to the direction of oscillation, so as to minimize the variation in the distance separating the beads. (e) This pair of rowers is compared with a single unaltered rower that experiences an oscillating flow, which is then scanned in frequency (detuned versus the rower). (d) The applied flow has a square wave structure, with magnitude v_ext and a period 2N_fδt that gives its frequency f_ext; the time step for simulation is δt.