GABA-mediated tonic inhibition differentially modulates gain in functional subtypes of cortical interneurons

Significance

GABA (γ-aminobutyric acid) is the brain’s predominant inhibitory neurotransmitter and exerts a strong inhibitory influence through extrasynaptic GABA_A receptors. This form of neurotransmission is known as tonic inhibition. Tonic inhibition is usually thought to reduce the excitability of all neurons, but here we show that it can selectively modulate the excitability of different types of neurons. Surprisingly, tonic inhibition can increase excitability in a common subtype of interneuron, and modeling results suggest this is achieved through the neuron’s electrophysiological, or functional, properties. These results provide insight into the impact of tonic inhibition upon neural activity and suggest a mechanism through which GABA may modulate the excitability of neurons in a selective manner.

Abstract

The binding of GABA (γ-aminobutyric acid) to extrasynaptic GABA_A receptors generates tonic inhibition that acts as a powerful modulator of cortical network activity. Despite GABA being present throughout the extracellular space of the brain, previous work has shown that GABA may differentially modulate the excitability of neuron subtypes according to variation in chloride gradient. Here, using biophysically detailed neuron models, we predict that tonic inhibition can differentially modulate the excitability of neuron subtypes according to variation in electrophysiological properties. Surprisingly, tonic inhibition increased the responsiveness (or gain) in models with features typical for somatostatin interneurons but decreased gain in models with features typical for parvalbumin interneurons. Patch-clamp recordings from cortical interneurons supported these predictions, and further in silico analysis was then performed to seek a putative mechanism underlying gain modulation. We found that gain modulation in models was dependent upon the magnitude of tonic current generated at depolarized membrane potential—a property associated with outward rectifying GABA_A receptors. Furthermore, tonic inhibition produced two biophysical changes in models of relevance to neuronal excitability: 1) enhanced action potential repolarization via increased current flow into the dendritic compartment, and 2) reduced activation of voltage-dependent potassium channels. Finally, we show theoretically that reduced potassium channel activation selectively increases gain in models possessing action potential dynamics typical for somatostatin interneurons. Potassium channels in parvalbumin-type models deactivate rapidly and are unavailable for further modulation. These findings show that GABA can differentially modulate interneuron excitability and suggest a mechanism through which this occurs in silico via differences of intrinsic electrophysiological properties.

GABA (γ-aminobutyric acid) is the predominant inhibitory neurotransmitter of the mammalian brain and regulates neuronal excitability through two modes of transmission: phasic and tonic inhibition (1). Phasic inhibition is mediated by the release of presynaptic GABA that activates GABA_A and GABA_B receptors within the postsynaptic and perisynaptic membrane. Tonic inhibition is mediated by extracellular, or “ambient,” GABA that diffuses throughout the extracellular space and activates GABA_A and GABA_B receptors within the extrasynaptic membrane (2, 3). Tonic inhibition exerts a powerful neuromodulatory influence across most brain regions, including the cerebral cortex, hippocampus, cerebellum, and thalamus (4).

Extrasynaptic GABA_A receptors that contribute to tonic inhibition possess unique subunit composition, electrophysiologic, and pharmacologic properties compared with postsynaptic GABA_A receptors (1, 5). Most extrasynaptic GABA_A receptors contain α5, α4, or δ subunits, and the presence of these subunits is thought to confer high affinity, which permits detection of micromolar concentrations of ambient GABA, and low efficacy, which enables high potential for allosteric modulation (1, 5, 6). A curious feature of the current passed by extrasynaptic GABA_A receptors is outward rectification at suprathreshold membrane voltage (7–13). Outward rectification enables greater inhibitory (hyperpolarizing) current to flow during action potential (AP) generation; however, its precise impact upon neuronal function is unclear. The extent of rectification may vary with GABA_A receptor subunit composition and is thought to be due to a voltage-gating mechanism (14).

Tonic inhibition carries broad clinical and pharmacological significance (15). Extrasynaptic GABA_A receptors are a primary target of anesthetic and some antiseizure agents, mutations cause inherited forms of epilepsy, and neurosteroid modulation can predispose to psychiatric disease or be utilized for therapeutic potential (5, 16). Recently, a positive allosteric modulator of extrasynaptic GABA_A receptors has shown benefit in postpartum depression, and an antagonist is undergoing a phase 2 clinical trial in poststroke motor recovery (17, 18).

Given the importance of tonic inhibition to neuronal function and its clinical relevance, there is much interest into how tonic inhibition modulates neuronal excitability (7, 8, 19–23). Neuronal excitability is often quantified using measures of rheobase and gain (19, 22, 23). Rheobase is defined as the minimum input that elicits an AP, and gain is the responsiveness of the neuron’s firing rate to changes of input. Within excitatory pyramidal cells, previous work has shown that tonic inhibition primarily modulates excitability by increasing rheobase (7, 19, 23). Nonrectifying inhibition, which obeys an ohmic (or linear) current–voltage (I–V) relationship, can reduce gain during random stimuli that approximate in vivo conditions by attenuating fluctuations in subthreshold input (19, 22, 23).

Within some inhibitory interneurons, the presence of tonic inhibition has been observed to increase firing frequency (8, 9). This counterintuitive finding is explained by a depolarized GABA reversal potential relative to resting membrane potential, allowing extracellular GABA to raise membrane voltage closer to AP threshold and reduce rheobase (24). It is possible this excitatory influence of GABA may be restricted to certain subtypes of interneurons (8). This is of significance for understanding the impact of tonic inhibition upon network activity given the emerging role of interneuron subtypes for selectively fine-tuning thalamocortical computations and neural information flow (25–27).

In light of this proposed role of tonic inhibition for modulating interneuron function, the objective of this study was to characterize the impact of tonic inhibition upon the excitability of different subtypes of cortical interneurons. Interneuron subtypes may be classified according to expression of molecular markers (for example parvalbumin or somatostatin), morphology, or functional (electrophysiological) properties (28). With respect to their electrophysiological properties, interneurons may be broadly categorized into either fast-spiking or non–fast-spiking subtypes, although further fine-grained subcategories exist, as given by the Petilla nomenclature (29).

Using biophysically detailed interneuron models, we predict that tonic inhibition can reduce gain in fast-spiking interneurons but, surprisingly, increase gain in non–fast-spiking interneurons. These predictions are supported by experimental patch-clamp recordings from layer 2/3 cortical interneurons. Further in silico analysis suggests that gain modulation in models occurs through a dendritic mechanism, is dependent upon differences in neuronal AP dynamics, and is enhanced by the presence of a large tonic current at depolarized membrane potentials—a property associated with outward rectifying GABA_A receptors.

Results

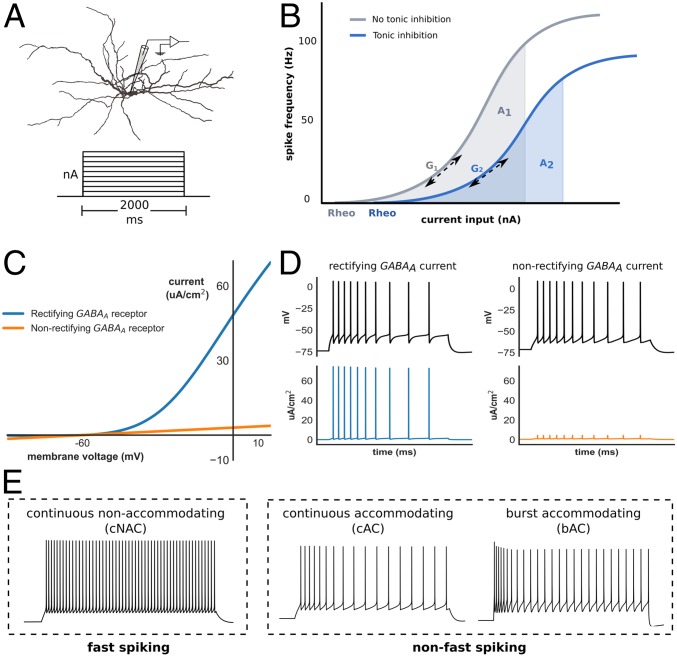
To investigate the impact of tonic inhibition upon interneuron excitability, we generated biophysically detailed interneuron models that were optimized to replicate the electrophysiological features of common subtypes (“E-types”) of cortical interneurons (Fig. 1A). We generated 10 fast-spiking interneuron models (“continuous nonaccommodating” or cNAC, using Petilla nomenclature) and 10 models of two subtypes of non–fast-spiking interneurons (“continuous accommodating” and “burst-accommodating,” or cAC and bAC, respectively; Fig. 1E).

Fig. 1.

Interneuron modeling and measurement of gain. (A) Interneuron model morphology and step-current protocol used to obtain the I–F relationship. (B) The I–F relationship was obtained with (blue) and without (gray) tonic inhibition, and the normalized change in gain (Δ gain) defined as either the change in AUC (from A₁ to A₂) across a fixed input range, or the change in gradient (G₁ to G₂) at a spike frequency of 20 Hz (Methods; rheo denotes rheobase). (C) I–V relationship of rectifying (blue) and nonrectifying (orange) extrasynaptic GABA_A receptors. (D) Rectifying extrasynaptic GABA_A receptors allow greater outward (hyperpolarizing) current to be passed at transmembrane voltages above approximately −50 mV, such as during AP generation. (E) Time–voltage traces of three models optimized to exhibit different interneuron E-type classified according to either fast-spiking vs. non–fast-spiking categories, or Petilla E-type. Note: by convention, hyperpolarizing transmembrane current is positive.

Several approaches exist to quantify the gain of a neuron’s input-frequency (I–F) relationship. Methods based on area under the curve (AUC) have the advantage of allowing simple comparison between I–F curves of different shape but may neglect changes at specific frequencies. Therefore, to assess the impact of tonic inhibition upon neuronal gain, the normalized change in gain (∆ gain) in the presence of tonic inhibition was calculated using two methods: one based on AUC and another on the gradient of the I–F curve (Fig. 1B; results use AUC, unless stated otherwise). To assess the impact of outward rectifying extrasynaptic GABA_A receptors upon neuronal gain, ∆ gain was also calculated using both a rectifying and nonrectifying conductance that generated similar change in neuronal rheobase (Methods, Detailed Neuron Modeling). As shown in Figs. 1C and 2D, the presence of rectification enables the model to generate a large inhibitory conductance at depolarized membrane potential.

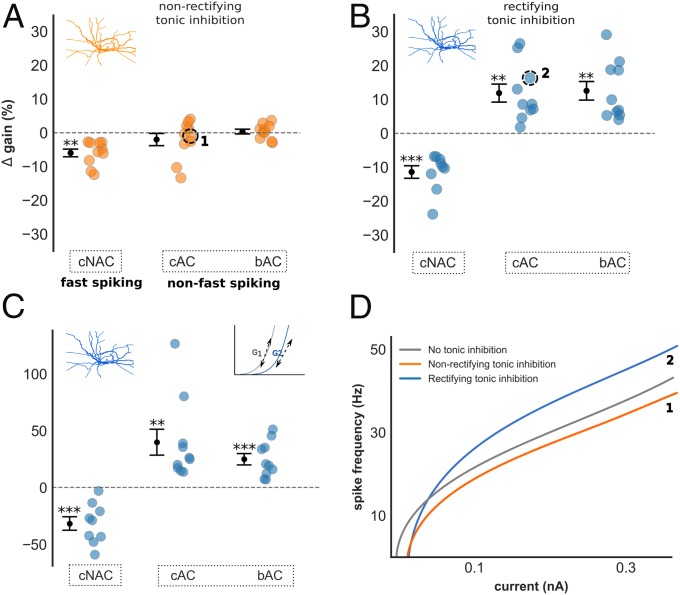
Fig. 2.

Impact of tonic inhibition on gain in interneuron models. (A–C) ∆ gain of all interneuron models grouped by E-type with nonrectifying (A) and rectifying (B) tonic inhibition. (A) Nonrectifying tonic inhibition had insignificant impact upon gain in non–fast-spiking models, and reduced gain in fast-spiking models. A small but significant difference in ∆ gain was observed between fast-spiking and non–fast-spiking models [−6.0% ± 1.1 vs. −0.8% ± 0.9; Welch’s t test, t₍₂₈₎ = −3.4, P < 0.01]. (B) In contrast, rectifying tonic inhibition increased gain in non–fast-spiking models, and differentially modulated gain between fast-spiking and non–fast-spiking models (−11.4% ± 1.8 vs. 12.2% ± 1.9; P < 0.001). (C) Differential gain modulation between fast-spiking and non–fast-spiking models persisted if ∆ gain was instead measured using the gradient of the I–F curve [−31.7% ± 6.0 vs. 32.4% ± 6.3; Welch’s t test, t₍₂₈₎ = −6.2, P < 0.001]. (D) Current–frequency relationship of one cAC (non–fast-spiking) model demonstrating changes in gain with nonrectifying (orange, labeled 1) and rectifying (blue, labeled 2) tonic inhibition. Results are presented as mean ± SEM. Asterisk denotes a significant ∆ gain value compared with ∆ gain = 0%; one-sample t test, *P < 0.05, **P < 0.01, ***P < 0.001.

Tonic Inhibition Differentially Modulates Gain in Functional Subtypes of Interneuron Models.

Consistent with previous studies exploring the influence of an inhibitory conductance upon neuron excitability (19), nonrectifying tonic inhibition did not produce a significant change of ∆ gain within non–fast-spiking models. A small reduction of ∆ gain was observed in fast-spiking models [−6.0% ± 1.1; one-sample t test, t₍₉₎ = −5.3, P < 0.001; Fig. 2A], and there was a small but significant difference in ∆ gain between fast-spiking and non–fast-spiking models [−6.0% ± 1.1 vs. −0.8% ± 0.9; Welch’s t test, t₍₂₈₎ = −3.4, P < 0.01].

Remarkably, rectifying tonic inhibition increased gain within non–fast-spiking models and induced large differences in ∆ gain between fast-spiking and non–fast-spiking models [−11.4% ± 1.9 vs. 12.2% ± 1.9; Welch’s t test, t₍₂₈₎ = −7.7, P < 0.001; Fig. 2B]. A difference in ∆ gain between fast-spiking and both non–fast-spiking Petilla E-types was also observed [one-way ANOVA with post hoc Tukey test, F_(2,27) = 28.9, P < 0.001], and these findings persisted if gradient was instead used to calculate gain (Fig. 2C). Rectifying tonic inhibition, therefore, differentially modulated the gain of fast-spiking and non–fast-spiking models. Interestingly, this excitatory influence upon non–fast-spiking models was also observed in the presence of a GABA reversal potential hyperpolarized relative to resting membrane potential (E_GABA of −80 mV; SI Appendix, Figs. S1 A and B and S5G). A hyperpolarized E_GABA is usually associated with reductions of neuronal excitability through increased rheobase, but our findings suggest a mixed inhibitory (increased rheobase) and excitatory (increased gain) influence (SI Appendix, Fig. S5H).

We investigated the relationship between rectification and gain modulation by varying the extent of rectification and recalculating ∆ gain in bAC models (SI Appendix, Fig. S1 E and F). Increased rectification produced a stepwise increase of ∆ gain in all models and a significant difference persisted with just 25% rectification (Wilcoxon signed-rank test, Z = 0.0, P < 0.01), suggesting gain modulation is related to the magnitude of tonic current generated at depolarized membrane potentials. To test this hypothesis, we repeated this analysis but used nonrectifying inhibition of increasing peak conductance. Here, due to linearity, large inhibitory current is passed at both depolarized and hyperpolarized potentials (SI Appendix, Fig. S8 A–C). Although increased gain was seen in some models, physiologically unrealistic increases of rheobase occurred due to large subthreshold inhibitory current (SI Appendix, Fig. S8 D and E). These modeling results suggest that gain modulation is dependent upon the magnitude of inhibitory current generated at depolarized membrane potentials, and that rectification may confer this property while preserving the ability to respond to normal levels of stimulating input.

We observed gain modulation in models under the assumption that ambient GABA acts upon the spatial extent of the neuronal membrane (1, 30). Therefore, we next investigated how varying the spatial distribution of GABA impacts neuronal excitability. This was achieved by restricting tonic inhibition to either the soma or dendritic compartment of each model and recalculating ∆ gain (Methods). Interestingly, differential gain modulation was observed if rectifying inhibition was distributed throughout the dendritic compartment, but not if restricted just to the soma (SI Appendix, Fig. S1 C and D). Here, we have assumed a spatially uniform density of extrasynaptic GABA_A receptors and so tonic inhibition generates much larger total conductance across dendrites due to greater surface area. Nevertheless, these results imply that, when the conductance density of tonic inhibition is uniform, gain modulation in silico is primarily mediated through the effects of GABA upon the dendritic tree.

Since neurons in vivo are exposed to random synaptic input rather than constant current often used during experimental recordings, we next investigated the impact of tonic inhibition upon gain in response to noisy input conditions (SI Appendix, Fig. S2A and Methods) (31). Again, rectifying tonic inhibition increased gain in non–fast-spiking models and induced large differences in ∆ gain between fast-spiking and non–fast-spiking models (−9.3% ± 2.2 vs. 6.1% ± 1.5; Welch’s t test, t₍₂₈₎ = −5.7, P < 0.001), and a significant difference in ∆ gain was observed between fast-spiking and both non–fast-spiking Petilla E-types [one-way ANOVA with post hoc Tukey test, F_(2,27) = 18.5, P < 0.001; SI Appendix, Fig. S2 C and D]. The presence of nonrectifying tonic inhibition also induced differences in ∆ gain between fast-spiking and non–fast-spiking models; however, differences were lower compared with rectifying tonic inhibition and increased ∆ gain within non–fast-spiking models not observed [SI Appendix, Fig. S2B; −5.4% ± 1.0 vs. −0.7% ± 0.4; Welch’s t test, t₍₂₈₎ = −4.4, P < 0.001].

These findings demonstrate that tonic inhibition can differentially modulate gain within neuron models optimized to replicate features of different cortical interneuron E-types. Gain modulation is dependent upon the model’s intrinsic electrophysiological properties, is mediated through dendrites, and is enhanced by a large inhibitory conductance at depolarized membrane potentials—a property that is conferred by outward rectifying GABA_A receptors.

Tonic Inhibition Differentially Modulates Gain in Layer 2/3 Cortical Interneurons.

In light of these modeling results, we next investigated the impact of tonic inhibition upon gain within interneuron subtypes of mouse somatosensory cortex. This was achieved by performing current-clamp recordings from layer 2/3 Sst-positive (n = 11) and Pv-positive (n = 10) interneurons. Each interneuron was then classified as fast-spiking or non–fast-spiking, and also according to its Petilla E-type.

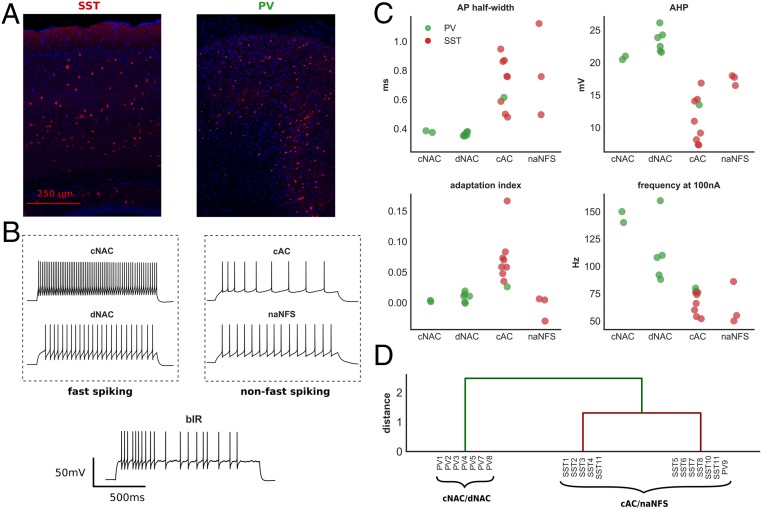
We identified five distinct Petilla interneuron E-types from our recorded cells (Fig. 3B): cNAC (n = 2), delayed nonaccommodating (dNAC) (n = 6), cAC (n = 9), nonadapting non–fast-spiking (naNFS) (n = 3), and burst-irregular (bIR) (n = 1). cNAC and dNAC interneurons are considered fast-spiking, and all were Pv-positive. cAC and naNFS are considered non–fast-spiking, and apart from one cAC interneuron, all were Sst-positive. Although bIR interneurons may be considered non–fast-spiking, their precise classification is uncertain, and so this interneuron was considered separately in our analysis (32).

Fig. 3.

E-type classification of layer 2/3 cortical interneurons. (A) Cortical immunohistochemical stain taken from an Sst (Left)- and Pv (Right)-positive mouse. (B) Time–voltage traces from five recorded interneurons classified by E-type (all experimental recordings shown in SI Appendix, Fig. S3). (C) Four electrophysiologic features of recorded interneurons grouped by Petilla E-type. These features were used for hierarchical clustering (two Pv interneurons were excluded from this analysis; Methods). (D) Hierarchical clustering of recorded interneurons. Two major groups were identified: one consisting of cNAC and dNAC Petilla E-types, the other of cAC and naNFS E-types. This separation is supportive of our subjective Petilla classification and a division into fast-spiking and non–fast-spiking categories. AHP, afterhyperpolarization; frequency at 100 nA, spike frequency at 100 nA above rheobase.

To test the validity of our classification, we performed hierarchical clustering on the recorded interneurons using four electrophysiological features known to discriminate between fast-spiking and non–fast-spiking E-types⁠ (Fig. 3C and Methods). The bIR and one dNAC interneuron were excluded from this analysis (Methods). We identified greatest separation between two groups: one group containing all cNAC and dNAC E-types, the other containing cAC and naNFS E-types (Fig. 3D). This separation supports both our subjective Petilla classification and a division of these interneurons into fast-spiking and non–fast-spiking, respectively (32).

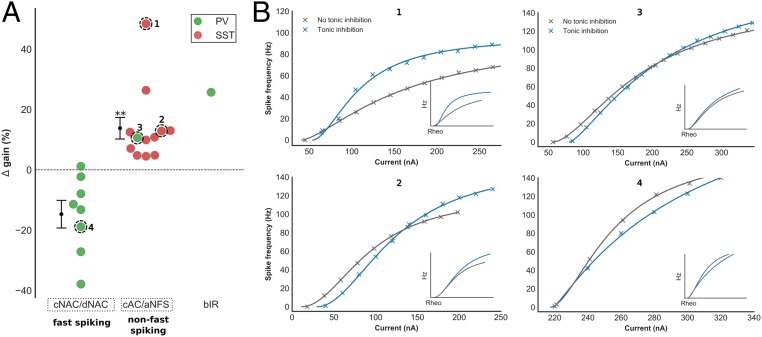
We then determined the impact of tonic inhibition upon neuronal gain by recording the input–frequency (I–F) relationship of all interneurons before and after blockade of extrasynaptic GABA_A receptors (Methods). I–F curves were fitted using a Hill-type function and ∆ gain calculated using both AUC and gradient, similar to our models. In contrast to previous studies investigating the impact of tonic inhibition upon the gain of excitatory pyramidal cells, we observed a wide range of ∆ gain values in recorded interneurons (Fig. 4A; time–voltage traces, I–F relationships, and electrophysiologic characteristics of all cells in SI Appendix, Fig. S4 and Table S1). Similar to our modeling results, tonic inhibition increased ∆ gain within non–fast-spiking interneurons (13.8% ± 3.6; Wilcoxon signed-rank test, Z = 0.0, P < 0.01) and differentially modulated ∆ gain between fast-spiking and non–fast-spiking interneurons (two-sided Mann–Whitney U test, U = 0, P < 0.001; Fig. 4A). Again, these findings persisted regardless of the measure used to calculate ∆ gain (SI Appendix, Fig. S3 A and B). Importantly, we observed increased ∆ gain within a Pv-positive cAC interneuron, suggesting that increases of ∆ gain are not dependent upon other neuronal properties determined by molecular marker (28). We also observed a large increase in ∆ gain within the bIR interneuron.

Fig. 4.

Impact of tonic inhibition on gain in layer 2/3 cortical interneurons. (A) Experimental changes in gain with tonic inhibition in fast-spiking (cNAC/dNAC), non–fast-spiking (cAC/naNFS) and bIR interneuron, colored by molecular marker (red, Sst; green, Pv). The current–frequency relationship of four interneurons are shown in B (Inset: adjusted for rheobase). The presence of tonic inhibition increased gain in non–fast-spiking compared with fast-spiking interneurons (two-sided Mann–Whitney U test, U = 0, P < 0.001). Increased gain was observed in a non–fast-spiking Pv interneuron (3), suggesting that differential gain modulation is not dependent upon other neuronal properties that vary with molecular marker. Tonic inhibition also increased gain within the bIR interneuron. Current–frequency relationships for all recorded interneurons are shown in SI Appendix, Fig. S3. Asterisk denotes a significant ∆ gain value compared with ∆ gain = 0%. *P < 0.05, **P < 0.01, and ***P < 0.001.

Gain modulation in silico was associated with outward rectifying GABA_A receptors due to their ability to conduct large current at depolarized membrane potentials. Therefore, we looked for outward rectification in layer 2/3 cortical interneurons by recording the I–V relationship of nine Sst interneurons before and after blockade of extrasynaptic GABA_A receptors with picrotoxin (Methods). Here, the subtracted I–V curve denotes the picrotoxin-sensitive component passed by extrasynaptic GABA_A receptors. We observed wide variation in the I–V relationship at depolarized membrane potentials (SI Appendix, Fig. S3D) and four interneurons displayed marked outward rectification.

Tonic Inhibition Enhances AP Repolarization and Reduces Voltage-Dependent Potassium Current in Neuron Models.

In contrast to the prevailing view, both our in silico and experimental results suggest that tonic inhibition can modulate neuronal gain in response to constant current stimuli (19). Most surprisingly, we observed increased gain within a potentially large subpopulation of inhibitory interneurons. Therefore, we performed further in silico analysis to explore the biophysical impact of tonic inhibition on models and seek a putative mechanism for gain modulation. This was achieved by computing the total membrane current at the somatic compartment during steady-state AP firing (Fig. 5 A and B). (Total membrane current is equivalent to the sum of ionic and axial currents that contribute to somatic membrane voltage [Fig. 5 F, Right].) We then calculated the change in total membrane current generated by the presence of tonic inhibition (denoted ∆ total membrane current; Fig. 5C).

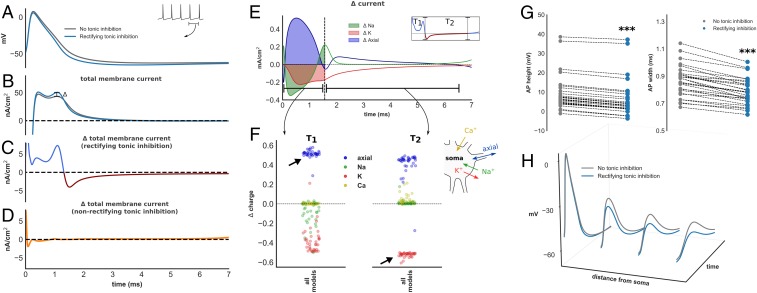
Fig. 5.

Biophysical impact of tonic inhibition. (A) Time–voltage trace during an interspike interval (ISI) in a model with (blue) and without (gray) dendritic rectifying tonic inhibition. Corresponding trace of total membrane current at the soma (B) and ∆ total membrane current with rectifying (C) and nonrectifying (D) tonic inhibition. Rectifying tonic inhibition enhances AP repolarization (C, blue trace T₁ and corresponding to positive ∆) and promotes earlier recovery from repolarization, reflected by a depolarizing change in total membrane current during AP downstroke (C, red trace T₂ and corresponding to negative ∆). (E) Changes in axial and ionic membrane current (∆ current) contributing to ∆ total membrane current (K and Na refer to all potassium and sodium conductances; leak and Ca were excluded since their contribution is minimal). (F) Normalized change in charge (Δ charge; Methods, Analysis of Detailed Models) for each ionic species during period T₁ and T₂. Enhanced AP repolarization is mediated by increased somato-dendritic axial current. The biophysical basis for this is shown in H: rectifying tonic inhibition attenuates electrotonic AP spread, increases somato-dendritic voltage gradient, and enhances axial current. In contrast, early recovery from AP repolarization is overwhelmingly mediated by reductions of (hyperpolarizing) potassium current (F). Reductions of potassium current are observed throughout the ISI (SI Appendix, Fig. S5B). (G) Reductions of AP height and width were observed in all models (P < 0.001), consistent with enhanced AP repolarization.

We found that rectifying inhibition increased the magnitude of outward (hyperpolarizing) total membrane current during AP generation in all models (i.e., positive ∆ total membrane current: blue trace in Fig. 5C, all models in SI Appendix, Fig. S5A). In contrast, nonrectifying inhibition produced much smaller change of ∆ total membrane current during AP generation (Fig. 5D). Rectifying tonic inhibition, in other words, appeared to enhanced AP repolarization. Consistent with this observation, a reduction of model AP height (Wilcoxon signed-rank test, Z = 0, P < 0.001) and AP width [one-sample t test, t₍₂₉₎ = 12.0, P < 0.001; Fig. 5G] was found. We also analyzed the AP phase portrait of all models and observed reductions of AUC (SI Appendix, Fig. S5 C and E). To determine the mechanism through which rectifying inhibition enhances AP repolarization in silico, we computed changes of current attributed to each ionic species at the soma in the presence of rectifying inhibition (Fig. 5E). We then calculated the change in charge, relative to total charge deposited across the membrane, for each ionic species and all models during enhanced AP repolarization (∆ charge, period T₁ in Fig. 5 E and F and Methods, Analysis of Detailed Models). Interestingly, we found that enhanced AP repolarization was mediated by increased somato-dendritic (axial) current (Fig. 5F). The biophysical basis for increased axial current is demonstrated for one model in Fig. 5H. Here, the presence of rectifying tonic inhibition attenuates the height of electrotonic spread of an AP down the model’s dendritic tree, a phenomenon previously demonstrated experimentally in hippocampal pyramidal neurons (30). This attenuation enhances the somato-dendritic voltage gradient and, by Ohm’s law, increases somato-dendritic current flow. We consider this effect in further detail in Discussion (SI Appendix, Fig. S8).

In addition to enhancing AP repolarization, we also found that rectifying tonic inhibition promoted earlier recovery from AP repolarization, reflected by an inward (depolarizing) change in total membrane current during the AP downstroke and afterhyperpolarization (AHP) (i.e., a negative ∆ total membrane current: outlined in red in Fig. 5C and SI Appendix, Fig. S5A). Using an identical approach, early recovery from AP repolarization in models was mediated by reductions of (hyperpolarizing) potassium current (period T₂, Fig. 5F). Importantly, we observed reductions of potassium current throughout the interspike interval (ISI) in all models (Fig. 5F, reductions in all channel subtypes for one model shown in SI Appendix, Fig. S5B). This is not surprising given the observed changes of AP morphology: a reduction of AP height and width affords less opportunity for activation of voltage-dependent potassium channels. Furthermore, this may confer significant impact upon the model’s excitability given changes in potassium current during the AHP have previously been associated with changes of neuronal gain (33–35). Since reductions of potassium current are a consequence of attenuation of AP electrotonic spread, this mechanism may also explain why gain modulation was only observed when tonic inhibition acted upon the model’s dendritic compartment.

In light of these in silico findings, we next investigated whether tonic inhibition exerts a similar biophysical impact upon interneurons recorded experimentally in brain slices. This was achieved by extracting AP features from experimentally recorded time–voltage traces before and after blockade of extrasynaptic GABA_A receptors with picrotoxin. Consistent with our models, we found that tonic inhibition produced a significant reduction of AP height (Wilcoxon signed-rank test, Z = 46, P < 0.05) and AP width [one-sample t test, t₍₂₀₎ = 2.6, P < 0.01; SI Appendix, Fig. S3C], suggesting a similar influence upon AP repolarization to that observed in silico. Finally, we analyzed the AP phase portraits of our experimentally recorded interneurons. Although we observed a narrowing of the AP phase portrait in 12 of 21 neurons, this did not reach statistical significance (SI Appendix, Figs. S4 and S5D; considered further in Discussion).

Differential Gain Modulation in Simplified Models Is Related to Variation in Magnitude and Deactivation Kinetics of Potassium Current.

Two biophysical consequences of rectifying tonic inhibition were identified in our detailed models: enhanced AP repolarization and reductions of transmembrane potassium current. However, these changes were evident across all models, and it therefore remains unclear why we observed divergent effects upon gain between fast-spiking and non–fast-spiking model E-types.

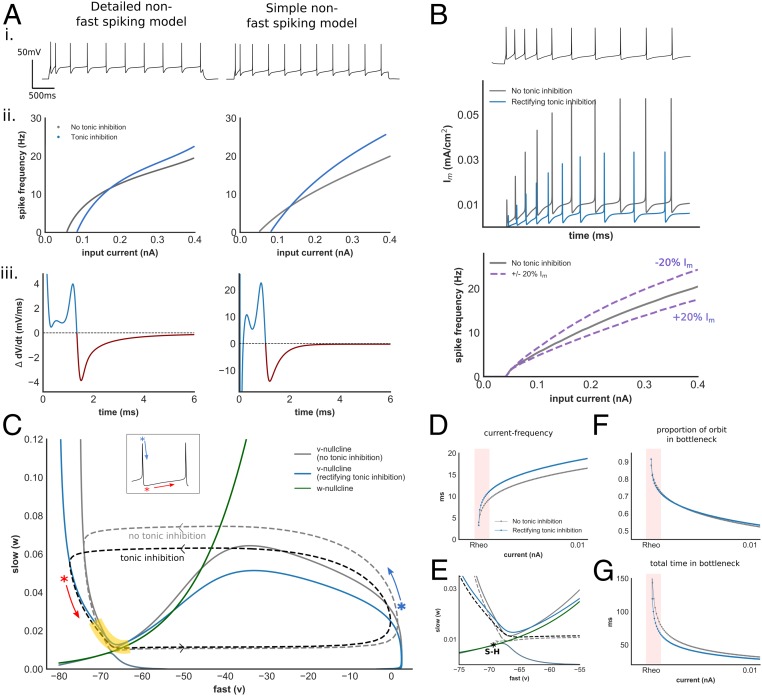
To address this question, we created simplified models of fast-spiking (cNAC) and non–fast-spiking (bAC) interneurons. Each model was optimized to reproduce the features of a detailed model with and without rectifying tonic inhibition (Fig. 6A). The simple models also exhibited similar changes in ∆ total membrane current: enhanced AP repolarization and early recovery from AP repolarization (Fig. 6A). The dynamics of each simple model are governed by three variables: fast (v, responsible for AP upstroke), slow (w, contributing to AP repolarization), and ultraslow (u, an I_m conductance that mediates spike-frequency adaptation). We achieved accurate fits between simple and detailed non–fast-spiking models if the kinetics of w were based on activation of the persistent potassium (K_P) current. For fast-spiking models, accurate fits were only achieved if the kinetics of w were based on activation of Kv_3.1 (Methods). We identified two mechanisms through which differential gain modulation may occur.

Fig. 6.

Modulation of AP dynamics with tonic inhibition within a simplified non–fast-spiking interneuron model. (A) Electrophysiologic features (i), I–F relationship (ii), and ∆ total membrane current (iii) within a simplified non–fast-spiking model and its detailed counterpart (simplified fast-spiking model in SI Appendix, Fig. S6A and parameter values in SI Appendix, Table S2). (B) I_m current generated by the non–fast-spiking model without (gray) and with (blue) tonic inhibition, and impact of changes of I_m current upon gain in this model (SI Appendix, Fig. S6B). (C) Phase-plane and orbits during AP generation of the v–w subsystem of the non–fast-spiking model, with and without tonic inhibition. Yellow denotes bottleneck region. Blue/red asterisks denote AP repolarization and AHP, respectively, corresponding to Inset time–voltage trace. (D) I–F relationship of the v–w system. Despite the absence of an ultraslow (I_m) current, tonic inhibition increases gain. (E) Phase-plane of the v–w system at the bottleneck. Transition from rest to spiking occurs via saddle–homoclinic (S–H) bifurcation (SI Appendix, Fig. S6E). Tonic inhibition reduces activation of w and alters the trajectory through this region. Proportion of total orbit (F) and time (G) spent within bottleneck with increasing input. Despite a similar proportion of the orbit spent within the bottleneck, the presence of tonic inhibition produced faster current–frequency scaling (pink region). This is reflected in a change in the eigenvalue of the unstable manifold of the S–H bifurcation (0.027 and 0.04 without and with tonic inhibition, respectively).

First, we found that tonic inhibition produced a similar proportional reduction of I_m current in both fast-spiking and non–fast-spiking models due to reductions of AP height and AP width (Fig. 6B and SI Appendix, Fig. S6B). However, the absolute value of I_m current is roughly an order of magnitude greater in the non–fast-spiking compared with fast-spiking model, due to a higher channel density (G_Im) required to generate spike-frequency adaptation (Fig. 6B). In support of this observation, we also found a higher density of channels mediating spike-frequency adaptation in our detailed non–fast-spiking models (SI Appendix, Fig. S5E). Crucially, varying the magnitude of I_m modulates gain, consistent with the known influence of a slow adapting current upon the neuronal I–F relationship (Fig. 6B) (36). Here, due to differences in magnitude of G_Im related to neuronal E-type, a similar proportional reduction of I_m current produces a far greater increase in gain within the non–fast-spiking model (SI Appendix, Fig. S6D).

Next, we examined the input–frequency relationship of the fast–slow (v–w) subsystem of each simple model, neglecting contribution from the ultraslow variable (Fig. 6C, SI Appendix, Fig. S6, and Methods). Interestingly, despite the absence of an I_m current, differential gain modulation between E-types persisted, suggesting another mechanism is also contributing (Fig. 6D). Analyzing the phase portraits of both models, we found that tonic inhibition reduced the activation of w, reflected in a narrowing of the height of the orbit during AP generation (Fig. 6C and SI Appendix, Fig. S6C). Since w mediates AP repolarization and the AHP, this change corresponds to reductions of voltage-dependent potassium current observed in our detailed models. Within both E-types, the I–F relationship is initially dominated by the presence of a bottleneck near the bifurcation from rest to spiking that allows for low-frequency firing (Fig. 6F and SI Appendix, Fig. S6F; highlighted in yellow in Fig. 6C and SI Appendix, Fig. S6C). In the non–fast-spiking model, w continues to deactivate slowly as the orbit traverses this bottleneck. By reducing the activation of w during AP generation, the presence of tonic inhibition alters the trajectory through this bottleneck, enhances frequency scaling, and increases gain (Fig. 6 E and G).

In contrast, w deactivates rapidly during the AP downstroke and AHP within the fast-spiking model. Rapid deactivation is due to faster deactivation kinetics associated with Kv_3.1 channels that are thought to enable high-frequency firing (28). Consequently, the orbit traverses the bottleneck adjacent to the w nullcline both with and without tonic inhibition (SI Appendix, Fig. S6 C and E). Similar to both the non–fast-spiking simple model and fast-spiking detailed models, tonic inhibition reduces the activation of w during AP generation. However, this exerts minimal impact upon frequency scaling since the trajectory through the bottleneck remains unchanged (SI Appendix, Fig. S6 F and G). A central prediction of this analysis is that Kv_3.1 contributes a smaller role toward AP repolarization within non–fast-spiking detailed models. Indeed, when comparing the ratio of K_P to Kv_3.1 conductance in our detailed models, we observed significantly higher ratios within non–fast-spiking compared with fast-spiking models (Mann–Whitney U test, U = 4.0, P < 0.001; SI Appendix, Fig. S5F). In contrast, the conductance density of Kv_3.1 ranged from 30- to over 100-fold greater than K_P in fast-spiking models, consistent with insight gained from our simple model that repolarization dominated by Kv_3.1 prevents tonic inhibition-mediated gain modulation.

In summary, enhanced AP repolarization and reductions of voltage-dependent potassium current differentially modulate gain in simplified models via two distinct mechanisms. First, reductions of “ultraslow” potassium current preferentially increase gain in non–fast-spiking models due to higher channel densities required to generate spike-frequency adaptation. Second, reductions of potassium current mediating AP repolarization and the AHP modulate gain according to channel deactivation kinetics. If there is rapid channel deactivation through Kv_3.1—a potassium channel known to be strongly expressed within fast-spiking interneurons (28, 37)—reductions in potassium current exert minimal influence upon gain.

Changes of Interneuron Gain Modulate Gamma-Frequency Oscillations in a Network Model.

Our modeling and experimental results have shown that tonic inhibition can unexpectedly modulate the gain of inhibitory interneurons. Interestingly, interneuron gain modulation has also been shown to occur in response to other neuromodulators such as acetylcholine and serotonin (33, 34). Although gain modulation of excitatory pyramidal cells is thought to subserve a number of behaviorally relevant changes in network activity, the influence of changes of interneuron gain upon activity within a neuronal network is less well established (38).

As a preliminary exploration of this question in light of our results, we explored the impact of interneuron gain within a network model consisting of excitatory (PC) and inhibitory (SST) neurons providing feedback inhibition (SI Appendix, Fig. S7A) (39). At sufficient input amplitude (I_stim) and recurrent excitatory conductance (G_pp), this network exhibits transient and sustained gamma-frequency oscillations (SI Appendix, Fig. S7B). We performed a sensitivity analysis to investigate the impact of 20% and 40% increases in SST gain. We found that increased SST gain produced a wider parameter range over which gamma oscillations could be sustained (SI Appendix, Fig. S7C). Interestingly, it has recently been shown that activation of Sst interneurons may promote cortical gamma-frequency local field potentials (40).

Discussion

Using biophysically detailed neuron models, we predict that tonic inhibition can modulate the gain of cortical interneurons. Unexpectedly, tonic inhibition increased gain in models with features typical for Sst interneurons but reduced gain in models with features typical for Pv interneurons. We then observed similar gain modulation in experimental recordings from Sst- and Pv-positive layer 2/3 cortical interneurons. Therefore, in contrast to the prevailing view, these results suggest that tonic inhibition can differentially modulate gain in subtypes of interneurons (19, 21–23).

Interestingly, our in silico analysis suggests that differential gain modulation is dependent upon the intrinsic electrophysiological properties of interneurons. This finding is of particular significance when considering the neuromodulatory action of ambient GABA. Ambient GABA diffuses throughout the extracellular space, and fluctuations in concentration exert profound influence over the excitability of cortical neurons (2). These fluctuations are driven by GABA transporter activity, synaptic spillover, and volume transmission from neurogliaform cells (1, 41). Instead of providing a simple “blanket” of inhibition, the nonspecific diffusion of GABA may selectively tune interneuron excitability. Although other neuromodulators, such as acetylcholine, can mediate selective interneuron excitation via cell-to-cell variation in receptor expression, GABA may achieve a similar feat through cell-to-cell variation in electrophysiological properties (42, 43).

Given the important influence of GABA upon brain function, these findings imply that differential excitation of interneuron E-types may promote behaviorally relevant network activity. A growing literature suggests that many neuromodulators regulate the excitability of interneuron subtypes to produce transitions in network activity (28, 43, 44). However, interneuron subtypes are typically defined according to characteristic molecular markers, for instance, through optogenetic manipulation of Pv- or Sst-expressing neurons (25, 27). Our results extend this concept and suggest that interneuron subtypes defined through electrophysiologic characteristics may also undergo selective modulation in vivo.

Our modeling suggests that a large inhibitory conductance at depolarized membrane potential can exert an important influence upon neuronal excitability. Similar to previous studies, we found that a small inhibitory conductance with a linear I–V relationship increased neuronal rheobase but had minimal impact upon neuronal gain (19, 21). Here, during spike generation, a small inhibitory current exerts minimal impact upon AP dynamics due to the comparatively large sodium and potassium currents that mediate AP upstroke and repolarization (19, 21). In contrast, we found that a large inhibitory current could alter a model’s AP morphology. Although this large current also produced physiologically unrealistic increases of rheobase with a linear I–V relationship (SI Appendix, Fig. S8), the presence of outward rectification preserved the model’s ability to respond to normal levels of stimulating input. Therefore, we hypothesize that rectifying extrasynaptic GABA_A receptors may enable GABA-mediated gain modulation during physiologically relevant input conditions.

Interestingly, rectifying tonic inhibition modulated neuronal excitability in silico by attenuating the amplitude of AP electrotonic spread through the dendritic compartment. Tonic inhibition has previously been shown to attenuate backpropagating APs in hippocampal pyramidal neurons and, in this context, may influence synaptic plasticity (30). In the present study, AP attenuation in computational models increases “axial” current between the soma and dendritic compartments. This axial current enhanced AP repolarization and reduced the activation of voltage-dependent potassium channels. We found indirect experimental evidence to support enhanced AP repolarization in vitro via reductions of AP height and width (SI Appendix, Fig. S3C). Although most recorded neurons showed similar changes of phase portrait AUC to models, this did not reach statistical significance (SI Appendix, Figs. S4 and S5D). Depending on the precise time course and magnitude of increased axial current during AP generation, enhanced AP repolarization could conceivably lead to reductions of AP upstroke velocity or height, or an increase of AP downstroke velocity. Such variation may contribute to differences in AUC between models and experiment, and further work is therefore required to demonstrate direct proof of our proposed mechanism and conditions under which it holds. For instance, our models also suggest that dendritic morphology and the distribution of GABA_A receptors influence the magnitude of axial current, as shown in SI Appendix, Fig. S9. Here, more extensive branching morphology is predicted to enhance axial current and AP repolarization, raising the possibility that tonic inhibition may exert a more pronounced effect upon excitability in neurons with greater dendritic arborization.

By generating models with a range of electrophysiological properties, we show theoretically that tonic inhibition can selectively enhance neuronal excitability in non–fast-spiking models despite exerting similar biophysical effects upon dendritic AP attenuation and potassium channel activation in all models. Two properties were identified that enable tonic inhibition to selectively increase gain in non–fast-spiking models. The first is the magnitude of an “ultraslow” conductance that generates spike-frequency adaptation within non–fast-spiking interneurons. Previous work has shown that ultraslow adapting currents can reduce gain (36). Here, we show that tonic inhibition can deactivate such currents through changes in AP morphology to increase gain. The second relates to differences in deactivation kinetics of repolarizing potassium currents. Our simplified fast-spiking model could only reproduce features of its detailed counterpart if kinetics of the slow variable (w) were based upon Kv_3.1. Notably, we then discovered a higher proportion of Kv_3.1 in our detailed models (SI Appendix, Fig. S5F), and this channel is known to be strongly expressed within fast-spiking interneurons (37, 45). Although tonic inhibition reduces the activation of w, this had minimal influence upon gain since w (Kv_3.1) deactivates rapidly during the AHP, a property that enables fast-spiking interneurons to generate rapid spike frequencies (SI Appendix, Fig. S6 C and E) (45). In contrast, w deactivates slowly in the non–fast-spiking model, and reduced activation in the presence of tonic inhibition alters the trajectory through the bottleneck dominating the initial I–F relationship. Such bottlenecks (or attractor ruins) are well described within neuron models that sustain low-frequency firing and initial I–F scaling (i.e., gain) is related to the eigenvalue associated with the unstable manifold at bifurcation (46, 47). In our non–fast-spiking model, slow w deactivation allows tonic inhibition to increase the eigenvalue of the unstable manifold and enhance gain. It is possible these properties could be exploited through other pharmacologic means to enable gain modulation. Interestingly, acetylcholine and serotonin have also been shown to enhance gain and modify AHP morphology within non–fast-spiking interneurons (33, 34).

Although experimental I–V recordings demonstrated significant rectification in four of nine interneurons, a similar degree of gain modulation was observed in cortical interneurons compared with models with rectifying tonic inhibition. A possible reason that experimental gain modulation was perhaps even greater than expected could relate to chloride Goldman–Hodgkin–Katz rectification. We did not include the contribution of transmembrane chloride gradient to the GABA_A current in our computational models. However, since the concentration of intracellular chloride was low in our experimental recordings, this would be anticipated to produce a degree of outward current rectification in the absence of a voltage-gating mechanism (7). Since the extent of rectification due to voltage gating may be dependent upon GABA_A receptor subunit composition, it is possible that differential gain modulation could be enhanced by targeting specific GABA_A receptor subtypes, for instance through neurosteroids (15, 48).

It is possible that our results generalize across species and age. Our models were optimized to fit features derived from recordings from juvenile rat neocortex, yet our experimental results were obtained from adult mice. We observed expected age-related electrophysiological differences between model and experiment (49). AP width, for instance, was significantly shorter in our experimental recordings (Fig. 5G and SI Appendix, Fig. S3C). Nevertheless, our prediction of differential gain modulation held. This suggests that tonic inhibition may exploit conserved features of interneuron E-types to mediate gain modulation.

This study raises further questions. Tonic inhibition exerts strong influence upon neuronal excitability in the thalamus, and a differential role for Sst and Pv interneurons within this region is emerging (25). Our findings raise the possibility that ambient GABA may promote thalamo-cortical activity preferentially driven by Sst-positive thalamic reticular nucleus interneurons. Interneurons that express the ionotropic 5HT3_A receptor were not investigated in this study, but, given they possess similar electrophysiologic properties to Sst neurons, we would anticipate similar changes in gain to the Sst population (28). Although we observed indirect changes in experimental recordings to support the mechanism of gain modulation derived from our models, further work is needed to confirm the existence of this mechanism in vivo. A future possibility is to use optical electrophysiology to confirm our prediction of dendritic AP attenuation within non–fast-spiking interneurons in the presence of tonic inhibition (50). Finally, the impact of interneuron gain modulation upon cortical network activity remains unclear. A simple rate-based model suggests a role in modulating oscillatory activity, but further studies are required to elucidate these network-level effects.

Methods

Full methods and data can be found in SI Appendix, Methods. Access to other raw data are available upon request to the corresponding author.

Detailed Neuron Modeling.

A layer 2/3 basket cell available through the Blue Brain Project Neocortical Microcircuit portal was used for single-neuron optimization and simulation (51). Parameter values for model mechanisms are found in Markram et al. (52) and references therein. Simulations and analysis were performed using NEURON and Python (53). Rectifying tonic inhibition was modeled using channel kinetics based on Pavlov et al. (7) and nonrectifying inhibition as a passive conductance. Tonic inhibition was present in all compartments and GABA reversal potential (E_gaba) set to −60 mV, unless otherwise stated. The peak conductance of ion channel mechanisms were optimized using a feature-based multiobjective algorithm implemented through BluePyOpt (discussed further in SI Appendix, Methods) (54).

Gain Calculation.

I–F relationships of optimized models were obtained using current injected at the soma and a point process generating excitatory conductance noise. Noise was modeled as an Ornstein–Uhlenbeck stochastic process with parameters based on Destexhe et al. (31). I–F curves were calculated for two G_ton values: 0 and 0.001 S/cm² (referred as “without” and “with” tonic inhibition hereon). Gain was calculated using gradient or area under the I–F curve (AUC). Δ gain was defined as the change in gain with tonic inhibition, normalized to gain without tonic inhibition:

$$\mathrm{\Delta }\mathrm{gain}\left(\text{\%}\right)=100\times \frac{\mathrm{Gai}{\mathrm{n}}_2-\mathrm{Gai}{\mathrm{n}}_1}{\mathrm{Gai}{\mathrm{n}}_1},$$

where Gain₁ and Gain₂ denote I–F gain without and with tonic inhibition, respectively. The input range used to calculate AUC was defined from rheobase to a current that elicited a frequency of 100 Hz or produced depolarization block, and the same input range applied to I–F curves with or without tonic inhibition. This approach ensures that depolarization block does not produce misleading changes of Δ gain (SI Appendix, Fig. S10). The gradient of the I–F curve was calculated after fitting the I–F curve to a Hill-type function (19). Gradient was calculated at a frequency of 20 Hz, which represents a spike frequency commonly observed in vivo for interneurons in awake animals (55, 56). Gain was also calculated in experimental recordings using peak gradient of the I–F curve.

Experimental Animals and Brain Slice Preparation.

See SI Appendix, Methods.

Whole-Cell Patch-Clamp Electrophysiology.

Slices cut from Sst-positive and Pv-positive mice were transferred to a submerged recording chamber on an upright microscope (Slicescope Pro-1000; Scientifica) and perfused (2 mL/min) with artificial cerebrospinal fluid (aCSF) at 32 °C. Layer 2/3 interneurons were visually identified using fluorescence targeted patching with infrared-oblique illumination microscopy with a 40× water-immersion objective (Olympus) and a CCD camera (IEEE 1394; Foculus). Whole-cell patch-clamp recordings were made in voltage and current clamp modes using a PatchStar micromanipulator (Scientifica) and an Axon Multiclamp 700B patch-clamp amplifier (MDS). Data were acquired using pClamp software (v10; MDS) with a sampling rate of 50 kHz and low-pass Bessel filtered at 10 kHz (Digidata 1440a; Axon). Patch pipettes (4–7 MΩ; GC150F-10; Harvard Instruments) pulled using a Flaming/brown micropipette puller (model P-1000; Sutter Instruments). For current-clamp recordings, patch pipettes were filled with a solution consisting of the following (in mM): 125 K-gluconate, 4 KCl, 2 MgCl₂, 10 Hepes, 10 EGTA, and 0.3 GTP-Na (pH 7.3 and 300 mOsm). For voltage-clamp recordings, CsCl (15 mM; Sigma), TEA (10 mM; Tocris), and Qx314 (5 mM; Tocris) were added to the above internal solution.

Pharmacology and Characterization of Tonic Inhibition.

Extracellular blockade of α-amino-3-hydroxy-5-methyl-4-isoxazole-propionic acid (AMPA) and kainate receptors was achieved with 2,3-dihydroxy-6-nitro-7-sulfamoyl-benzo[f]quinoxaline-2,3-dione (NBQX) (50 µM; Sigma), N-methyl-d-aspartate (NMDA) receptors with (2R)-amino-5-phosphonopentanoate (AP5) (50 µM; Tocris), γ-aminobutyric acid B (GABA_B) receptors with CGP5243 (25 µM; Sigma), phasic GABA_A receptors with SR95531 (0.5 µM; Sigma), and extrasynaptic (tonic) GABA_A receptors with picrotoxin (100 µM; Sigma). GABA (5 µM; Tocris) was included in the aCSF solution to provide a basal level of GABA agonism. Once whole-cell configuration was obtained, to characterize the I–F relationship a holding current was injected to maintain a membrane potential of approximately −70 mV and current steps applied (−60- to 320-pA steps amplitude in 20-pA increments, 1-s step duration) in current-clamp mode. To characterize the I–V relationship, cells were held at −70 mV and a voltage ramp (from −70 to −20 mV; 5-s duration) and voltage step (from −70 to 30 mV; 1-s duration) applied. Series resistance and whole-cell capacitance compensation were applied. To be included in the study, a cell had to have an access resistance of less than 20 MΩ and a holding current of less than −200 pA throughout the entire recording. Current- and voltage-clamp protocols were performed before and after application of picrotoxin. Voltage dependence of the picrotoxin-sensitive current (i.e., extrasynaptic GABA_A-mediated current) was calculated by subtracting the I–V relationship before and after picrotoxin. Values presented are not corrected for liquid junction potential. The I–V relationship in SI Appendix, Fig. S3D is normalized for each cell relative to the picrotoxin-sensitive current at −70 mV.

Experimental Data Analysis and E-Type Classification.

Experimental data analysis was performed using Axograph X software (Berkeley) and the Electrophys Feature Extraction Library (EfEL) (52). Recorded neurons were classified using the Petilla classification by three coauthors of this study with complete interobserver agreement (A.B., C.A.R., and S.P.). Features for each neuron were extracted at rheobase (with the exception of frequency at 100 nA) using EfEL. Hierarchical clustering was performed using Ward’s method with four features: AP half-width, afterhyperpolarization potential, adaptation index, and frequency at 100 nA (32). PV10 was excluded from analysis since it had clearly distinct features to eye compared with other recorded cells, and PV6 excluded because a spike frequency 100 nA above rheobase was not obtained with the experimental protocol. ∆ gain was calculated in experimental recordings using the approach in Gain Calculation after fitting to a Hill function. Due to the sigmoidal shape of the I–F curve in many recorded Sst interneurons, to avoid misleading ∆ gain values when calculating AUC the lower input range was defined as the minimum input that elicited a spike frequency above 1 Hz.

Analysis of Detailed Models.

Detailed models were analyzed during constant current injection at the soma that elicited a spike frequency of 20 Hz with and without dendritic rectifying tonic inhibition. Axial current flow between the soma and a dendrite (d) was calculated using axial resistivity (R_i), somatic voltage (V_soma), and dendritic voltage (V_d). Total axial current at the soma (I_Ax) is therefore the sum of all axial currents:

$$I_{\mathrm{Ax}}={\displaystyle \sum }^d\frac{V_{\mathrm{soma}}-V_{\mathrm{d}}}{R_i}.$$

Total membrane current is defined as the sum of ionic (I_Ion), axial and injected current (I_stim). ∆ total membrane current was calculated by subtracting total membrane current with and without tonic inhibition during an ISI (Fig. 5B). To ensure calculation of ∆ total membrane current was not subject to numerical error, simulations were performed with a fixed time step (dt) of shorter duration until differences in waveform were no longer visible by eye. Results presented use a dt of 0.001 ms.

Changes in axial (∆ axial) and individual transmembrane ionic currents during an ISI were calculated using the same approach (Fig. 5E). To determine the contribution of axial and individual transmembrane ionic currents to ∆ total membrane current over T₁ and T₂, the normalized change in membrane charge transfer (∆ charge) was calculated. This represents the relative difference in charge deposited across the membrane for a given ionic species in the presence of tonic inhibition. For example, the contribution of axial charge transfer (∆ axial charge) over period T₁ is given by the following:

$$\mathrm{\Delta }\mathrm{axial}\hspace{0.17em}\mathrm{charge}=\frac{{{\displaystyle \int }}^{{\mathrm{T}}_1}\mathrm{\Delta }\mathrm{axial}\hspace{0.17em}\mathrm{current}}{{{\displaystyle \int }}^{{\mathrm{T}}_1}\left|\mathrm{\Delta }\mathrm{Na}\hspace{0.17em}\mathrm{current}\right|+\hspace{0.17em}{{\displaystyle \int }}^{{\mathrm{T}}_1}\left|\mathrm{\Delta }\mathrm{K}\hspace{0.17em}\mathrm{current}\right|\hspace{0.17em}+\hspace{0.17em}{{\displaystyle \int }}^{{\mathrm{T}}_1}\left|\mathrm{\Delta }\mathrm{axial}\hspace{0.17em}\mathrm{current}\right|}.$$

Calcium current is omitted as its contribution is negligible. The contribution of all ionic currents over period T₁ and T₂ was calculated in the same manner.

Simplified Neuron Modeling.

Simplified neuron models were developed in three stages. First, channel mechanism used in detailed models were reexpressed in terms of a variable that evolves over one of three timescales: fast (v), slow (w), and ultraslow (u). Second, single-compartment models containing these mechanisms were optimized to fit the features of a detailed bAC and cNAC model with and without tonic inhibition. Finally, optimized simple models were only analyzed if the model with tonic inhibition exhibited enhanced AP repolarization and early recovery from AP repolarization compared with the model without tonic inhibition, similar to their detailed counterparts (Fig. 6). Channel mechanisms were simplified using a technique based on separation of timescales and equivalent voltages (SI Appendix, Methods) (57, 58). Voltage-gated sodium channel activation responsible for AP upstroke is considered instantaneous with respect to voltage (v). Persistent potassium (K_P) activation (w) was used in the non–fast-spiking (bAC) model to govern dynamics of variables evolving over a slow timescale. For the fast-spiking (cNAC) model, the I–F relationship and AP features could only be reproduced if w was governed by kinetics of Kv_3.1 activation. Finally, I_m channel activation (u) evolves over an ultraslow timescale and determines spike-frequency adaptation. Parameters of simple models were optimized using a similar approach to Detailed Neuron Modeling. Here, features used to optimize detailed models were extracted from a detailed bAC and cNAC model with and without tonic inhibition and used as objectives for optimization of the simple models. For each optimized simple model, the sum of all feature errors was under 20, i.e., simplified models replicated features of detailed models more accurately than the detailed models replicated features from in vitro recordings. Phase plane analysis of the v–w subsystem of simple models was performed after freezing the ultraslow variable (u). Phase plane analysis was performed using XPPAUT (59). In Fig. 6E (and SI Appendix, Fig. S6E), the bottleneck is defined as a period of the trajectory that accounts for 90% of the duration of the orbit at rheobase.

Network Modeling.

See SI Appendix, Methods.

Statistics.

Results are presented as mean ± SEM. We based sample sizes for our modeling results on a pilot study of one fast-spiking and one non–fast-spiking model. Here, a Δ gain of approximately −10% and +10% was observed. Assuming variance of 5%, we calculated a sample of at least eight to ensure adequate power. For experimental studies, we used a similar sample size to our models under the assumption our models were predictive. Our sample sizes are also comparable to those reported in previous studies exploring the impact of a neuromodulator upon single-neuron excitability (9, 33, 42). Data were assessed for normality using the Shapiro–Wilk test. Significant changes of ∆ gain for individual E-types, changes of AP features, and phase plot AUC were calculated using either one-sample t test or Wilcoxon signed-rank test. Comparison between fast-spiking and non–fast-spiking E-types and conductance density ratio used Welch’s t test or Mann–Whitney U test. Differences were considered significant if *P < 0.05, **P < 0.01, and ***P < 0.001. n.s. denotes not significant.