Abstract
Rotating machines are critical equipment in many processes, and failures in their operation can have serious implications. Consequently, fault detection in rotating machines has been widely investigated. Conventional detection systems include two blocks: feature extraction and classification. These systems are based on manually engineered features (ball pass frequencies, RMS value, kurtosis, crest factor, etc.) and therefore require a high level of human expertise (it is a human who designs and selects the most appropriate set of features to perform the classification). Instead, we propose a system for condition monitoring and fault detection in rotating machines based on a 1-D deep convolutional neural network (1D DCNN), which merges the tasks of feature extraction and classification into a single learning body. The proposed system has been designed for use on a rotating machine with seven possible operating states and it proves to be able to determine the operating condition of the machine almost as accurately as conventional feature-engineered classifiers, but without the need for prior knowledge of the machine. The proposed system has also reported good classification on a bearing fault dataset from another machine, thus demonstrating its capability to monitor the condition of different machines. Finally, the analysis of the features learned by the deep model has revealed valuable and previously unknown machine information, such as the rotational speed of the machine or the number of balls in the bearings. In this way, our results illustrate not only the good performance of CNNs, but also their versatility and the valuable information they could provide about the monitored machine.
Keywords: Industrial engineering, Systems engineering, Artificial neural networks, Artificial intelligence, Signal processing, System fault detection, Process monitoring, Condition monitoring, Feature learning, Vibration analysis, Fault detection, Convolutional neural network
Industrial engineering; Systems engineering; Artificial neural networks; Artificial intelligence; Signal processing; System fault detection; Process monitoring; Condition monitoring; Feature learning; Vibration analysis; Fault detection; Convolutional neural network
1. Introduction
Detection and diagnosis of faults are useful to optimize and guarantee the safety in the operation of machines, leading to higher productivity and process efficiency, with benefits such as reduced operating costs, longer machine life or improved operating uptime [1]. Bearings are essential components in rotating machines and their failure is one of the most common causes of machinery breakdown [1], [2]. The presence of these elements induces inherent system vibrations, which are generated not only under normal operating conditions but also under fault conditions (external raceway faults, internal raceway faults, rolling element faults, cage faults, imbalances, misalignments, etc.). Vibration analysis is therefore often used to monitor the operation of rotating machines and thus to detect system faults [3], [4].
Frequency domain analysis is a widely adopted technique [5], [6], [7] for the study of system vibrations. It requires knowledge about the fundamental frequencies of the system and proposes to monitor the amplitude of vibrations at such frequencies in order to detect anomalies. Although this technique provides good results, it has significant disadvantages. For example, manually designed frequencies may differ slightly from the real frequencies of the machine, as the bearings operate under a combination of rolling and sliding [8]. Another source of error is the simultaneous presence of different types of faults as well as the interference from additional sources of vibration, both of which can obscure important frequencies in the spectrum [6]. Finally, some defects, such as lubrication ones, do not manifest themselves as a new frequency, making them very difficult to detect across the frequency spectrum [9].
These drawbacks reveal the weaknesses of methods based on manually engineered features, whose performance depends to a large extent on the quality of the selected features. This situation has led to numerous studies on the optimal choice of features and it has been demonstrated that, in certain contexts [10], [11], [12], [13], fault features can be successfully extracted by using traditional methods of analysis. However, efficient fault detection remains a challenge when systems are very complex. In such cases, choosing the right features is still a difficult task, as it requires expertise, prior knowledge of the machine and a strong mathematical basis.
Faced with this situation, there is a growing interest in feature learning [14]. It is an alternative approach to feature engineering, which proposes to learn the representation of discriminative features from raw input data, rather than designing them manually. Principal Components Analysis (PCA) [15], sparse coding [16], sigmoid belief networks [17] or auto-encoders [18] have been widely used for this purpose. But these traditional techniques are now being replaced by deep learning models, whose ability to find the best representations of data, known as representation learning [19], makes them powerful feature extractors. In fact, some deep models have already proven to be able to simplify feature engineering and successfully detect machine faults [20], [21], [22], [23], [24], [25]. The real challenge, however, is to completely eliminate feature engineering and it is in this field that Convolutional Neural Networks (CNNs) [26] stand out.
CNNs have recently become the default standard for deep learning tasks and have demonstrated an outstanding ability to detect patterns in images and signals. They have already been successful in other fields, such as image or voice recognition, and have achieved the best results with a significant performance gap with respect to state-of-the-art techniques [27], [28], [29]. Their ability to detect faults in rotating machines has also been the subject of several studies, but few papers further investigate the features learned by CNN models or the information they might provide about the nature of the machines [30], [31].
Under such circumstances, this article presents a system for condition monitoring and fault detection in rotating machines based on vibration and current analysis using a 1D DCNN. This system recognizes the condition of the machine, from raw operating data, with a 98% accuracy. Furthermore, we present the convolutional filter learned by the deep model, the study of which reveals key parameters of the machine, such as its rotational speed or the number of balls in the bearings. In addition, to assess this proposal we compare its performance with that of classic methods of fault detection based on manually engineered features (Multi-Layer Perceptron -MLP- [21], Random Forest Classifier -RFC- [32], and Support Vector Classifier -SVC- [33]) and our system proves to be able to determine the state of the machine almost as successfully as traditional classifiers, but without the need for prior knowledge of the machine. Finally, we test the behavior of the proposed system on another rotating machine, where it also reports a good classification (92% accuracy).
In summary, the contributions of this research are as follows: (1) we propose a system for condition monitoring in rotating machines that merges the tasks of feature learning and fault detection; (2) feature learning makes it possible to detect faults without human experience or prior knowledge of the machine and allows the system to be used in the monitoring of another rotating machine; (3) we analyze the features learned by the model and thus provide a priori unknown machine information (as far as we know, this is the pioneering work applied to this purpose).
The rest of this document is organized as follows. In Section 2, we introduce the concepts of feature engineering and feature learning, as well as the basic theory of deep convolutional neural networks. Section 3 presents the working dataset and describes the architecture of the proposed CNN model. The results of the model are shown in Section 4. Finally, the conclusions are set out in Section 5.
2. Related literature
2.1. Feature engineering
Bearing faults are the most frequent in rotating machines and also the most difficult to detect but, when detected early, they are the least expensive to repair [34]. In this context, machine learning algorithms are commonly used, as they can detect faults efficiently and automatically, based on a set of representative features of the machine. Features are extracted from raw machine operating data (typically, currents and vibrations, which are variables with a great deal of information about machine condition) and it is an expert, with expertise and prior knowledge about the machine, who decides which is the most appropriate set of features to extract [6]. They are therefore called manually engineered features.
Windowing is a widely used technique [35] in the feature extraction phase. According to it, data is split into windows, with or without overlap, and features are calculated for each window. In this context, RMS value [36], kurtosis [37] and crest factor [37] have proved to be useful in the detection of bearing faults. They are calculated according to equations (1)-(3), where x is a vector of N samples in a window, and μ and σ respectively denote the mean and standard deviation of x.
| (1) |
| (2) |
| (3) |
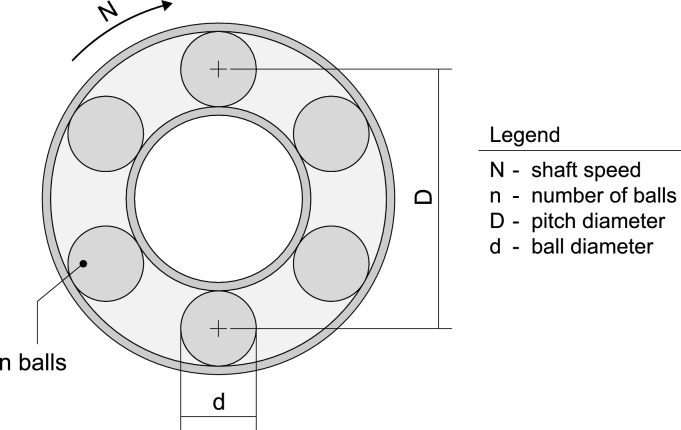
The monitoring of frequency features, like vibration amplitude at fault frequencies, also provides good results. When both bearing geometry and shaft speed are available (Fig. 1), these frequencies can be calculated according to the equations below (4)-(7) [38].
Figure 1.
Bearing geometry.
In (4) and (5) we observe the Inner (BPFI) and Outer (BPFO) Ball Pass Frequencies, which are related to defects in the inner and outer track of the bearing, respectively. These equations require some knowledge of the machine: N (shaft speed), D (pitch diameter), d (ball diameter) and n (number of balls in the bearing). Alternatively, if D and d are unknown, (4), (5) can be replaced by the experimental equations (6), (7) [2].
| (4) |
| (5) |
| (6) |
| (7) |
The above mentioned features are the most commonly used in the literature, but many more can be extracted from operating data (fundamental train frequency, ball pass frequency, skewness, shape factor, clearance factor, impulse indicator, etc.). It still requires a human expert to decide which are the most suitable for each problem. Machine learning algorithms are then fed with these features and, based on them, they monitor the condition of rotating machines in order to detect faults. Algorithms such as Support Vector Machines (SVMs), Decision Trees (DTs) or Multi-Layer Perceptrons (MLPs) have already proven their success in this field [21], [39], [40].
In short, the combination of feature engineering and machine learning algorithms results in useful condition monitoring tools that accurately detect different types of faults. However, these tools cannot be easily reused (they are highly problem-dependent) and their performances worsen when systems are complex or several faults occur simultaneously (detection becomes difficult [41]). Therefore, there is a need for more advanced analysis techniques, such as feature learning.
2.2. Feature learning
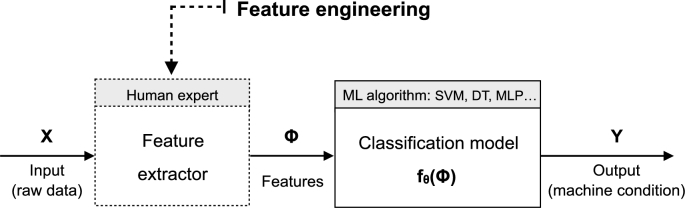
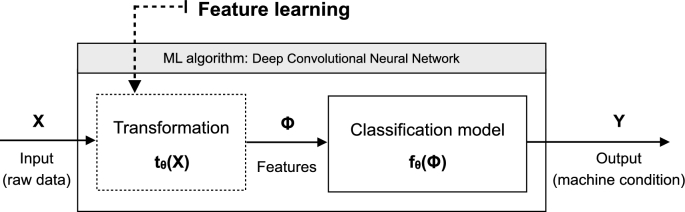
While in feature engineering features are designed and selected by experts, feature learning is about learning the transformation of raw data that leads to an optimal representation for the task to be performed. Fig. 2 and Fig. 3 illustrate these two approaches.
Figure 2.
Feature engineering approach.
Figure 3.
Feature learning approach.
As shown in Fig. 2, in the feature engineering approach it is an expert who extracts the features of interest ϕ from the raw input data X. These are then used to train a classification algorithm that returns the condition Y of the input data. The role of the Machine Learning (ML) algorithm is to learn the optimal parameters θ for the classification task.
The feature learning approach (Fig. 3) proposes to learn as well the transformation of the raw input data X that produces a suitable representation ϕ for the classification task . Therefore, in this case, the ML algorithm covers both classification and feature extraction tasks.
Several feature learning techniques have been proposed in the literature, such as Principal Components Analysis (PCA) [15], sparse coding [16], sigmoid belief networks [17] or auto-encoders [18]. But these techniques still need to be supplemented with additional algorithms in order to perform the classification. Instead, the nature of Convolutional Neural Networks gives them the ability to bring both feature learning and classification tasks together (Fig. 3). Therefore, we propose in this article a CNN-based model to detect faults in rotating machines.
2.3. CNNs for feature learning
CNNs have become one of the leading exponents of deep learning techniques, demonstrating great skill in feature learning. Fig. 4 shows the typical structure of a CNN model, consisting of three types of layers: convolutional, pooling, and fully connected layers. In the first place, there are the convolutional layers, whose role is to detect local conjunctions of features from the previous layers. So it is in these layers where feature learning resides. Then, they are followed by the pooling layers, which aim to merge semantically similar features together, thus reducing the dimensionality of the data and therefore the computational complexity of the model, as well as providing invariance to small shifts and distortions. Finally, there are the fully connected layers, which connect all the neurons in the previous layer to each of the neurons in the current layer in order to generate global semantic information.
Figure 4.
Example of CNN architecture for image recognition (each plane is a feature map).
By stacking several convolutional, pooling and fully connected layers, we obtain a compositional hierarchy, in which the higher level features are the composition of the lower level ones [14]. Accordingly, in images, local combinations of borders form motifs, motifs are assembled into parts, and parts form objects. In this way, CNNs perform high-level reasoning that allows them to successfully carry out the required task (image classification in Fig. 4). But CNNs are not only capable of detecting patterns in images. They have also proven successful in processing one-dimensional signals where, in a similar fashion as in 2D images, local combinations of components are hierarchically composed across layers to produce complex signal patterns, standing out in fields such as voice recognition [27]. It can therefore be assumed that this success could be transferred to other areas with similar signals and goals, as can be the detection of fault patterns in currents and vibrations coming from rotating machines.
Fig. 4 also shows how the layers are made up of simpler units, commonly known as neurons. Each of these units has a weight and a bias, which are the parameters to be learned by the model according to the process detailed below.
2.3.1. Learning process
During the learning process (or training of the model), a set of input samples and their corresponding expected outputs is presented to the model. The error between the expected outputs and the actual outputs of the model is quantified in terms of an error measure, such as the categorical cross-entropy error, which is the most suitable for classification problems [42], where it helps learning algorithms to converge faster. Gradient descent is then used to fit the learnable parameters of the model (weights and bias) so that the error is minimized [43], computing the gradient by means of backpropagation [44]. The way in which the model transforms inputs into outputs depends on the nature of its layers, whose peculiarities are described below.
In fully connected layers, each unit computes a linear combination of the input to the unit followed by a non-linear activation function, which gives the model the flexibility to estimate complex relationships in the data. Accordingly, the output vector of the lth layer (xl) is shown in (8), where: σ is the activation function, x is the input vector to the lth layer, Wl is the matrix containing all the weights of the connections between th and lth layers, and bl is the bias vector.
| (8) |
The difference with convolutional and pooling layers is that they are not fully connected (it can be seen in Fig. 4), which means that each unit in a layer does not receive incoming connections from all the units in the previous layer, but only from some of them. This allows each unit to specialize in only one region of the former layer. In this way, convolutional and pooling layers divide and model data into smaller parts [45], preserving the spatial coherence of the data [19] and drastically reducing the number of operations to be performed, as well as the number of parameters to be learned. In convolutional layers, learnable parameters are organized as a set of filters that convolve over a multichannel input (for example, the combination of several vibration signals), resulting in a set of vectors called feature maps (9). In this equation we see that the convolution (⁎) of the channel c of the input x and the mth filter of such channel W results in the mth output feature map x, being b the bias vector.
| (9) |
The subsampling operation is then performed on the pooling layer by means of a subsampling mask, which divides the input vector into patches and returns an aggregated value for each patch. The max pooling function [46], which returns the maximum value of incoming data on each patch, is the most commonly used in CNNs.
Finally, it is worth mentioning the presence of the activation function (σ) in the transformations between all layers in the model. In the output layer, functions such as sigmoidal (two-class classifiers) and softmax (multi-class classifiers) are mainly used. In the other layers, the ReLU function [47] has become the default choice. This function allows networks to easily obtain sparse representations of the data, helps to alleviate the vanishing gradient problem and accelerates the convergence of learning [48].
3. Proposed method
In this section we present the CNN architecture with which we approach the detection and diagnosis of faults in rotating machines. We also describe the working dataset on which this architecture has been tested.
3.1. Dataset
Our testing machine is shown in Fig. 5. It is a 4kW induction motor with 6306-2Z/C3 bearings that rotates at 1500 rpm (25 Hz) with a supply frequency of 50 Hz. This machine has been subjected to seven different tests (Table 1), for each of which three operating variables (Table 2) have been measured during 4 seconds at a sampling frequency of 5000 Hz (4 s ⋅ 5000 Hz = 20000 samples per test). In order for the three variables to have the same range and also in order to make the training faster and reduce the chances of the learning algorithm to get stuck in local optima, we pre-process the resulting dataset according to standard practice: we normalize the raw data, by means of min-max scaling [49] with range ; and then apply the windowing technique, with mean detrended windows [50] of 800 samples and no overlap.
Figure 5.
Testing machine.
Table 1.
Tests performed.
| Test ID | Machine condition |
|---|---|
| T1 | Mechanical fault (eccentric mass on pulley) |
| T2 | Combined electrical and mechanical fault |
| T3 | Normal operation |
| T4 | Electrical fault (5 ohm resistor in phase R) |
| T5 | Electrical fault (10 ohm resistor in phase R) |
| T6 | Electrical fault (15 ohm resistor in phase R) |
| T7 | Electrical fault (20 ohm resistor in phase R) |
Table 2.
Variables measured in the tests.
| Variable | Description |
|---|---|
| ax | Horizontal vibration acceleration |
| ay | Vertical vibration acceleration |
| ir | Phase R current |
3.2. CNN model
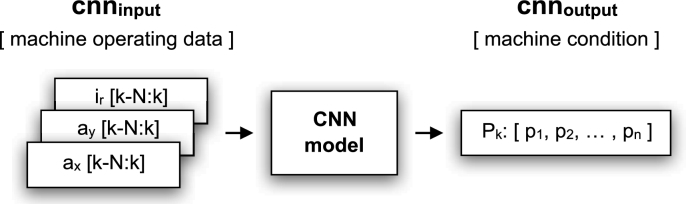
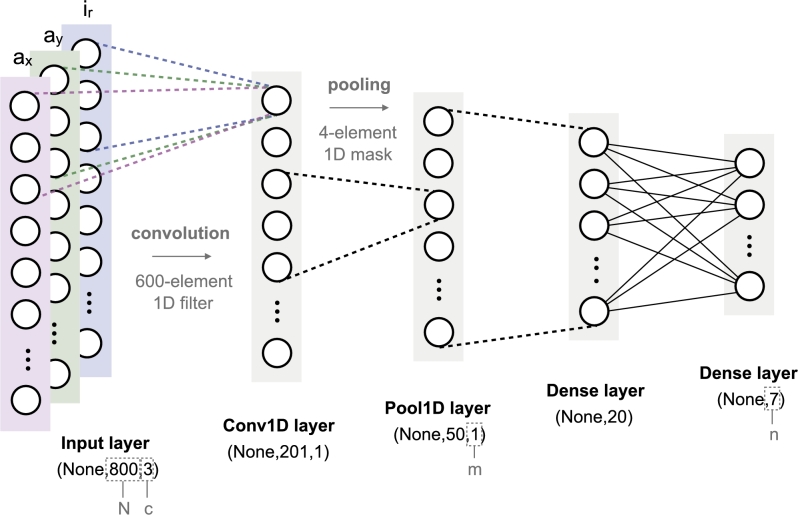
As described in Fig. 6, the proposed CNN model determines the condition of the machine, at any instant k, on the basis of an input vector containing machine operating data (current and vibration values). The input data vector has size , where N is the number of samples in a window () and c is the number of channels in the data (, since we have information on three variables: , , ) (Table 2). The model output is a vector of n elements, which reports the probability of the input vector to match each of the n possible machine states (, according to the seven tests performed) (Table 1).
Figure 6.
Working context of the CNN model.
To establish the correspondence between machine operating data and machine condition, we use the convolutional architecture shown in Fig. 7, which performs both feature learning and classification. This model consists of a 3-channel input layer and an output layer with 7 units. Feature learning is performed by means of a convolutional layer with a 600-element 1D filter and a max-pooling layer with a 4-element subsampling mask. The learned features are then classified using a fully connected layer of 20 units. The softmax activation function is used in the output layer and the ReLU function in the other layers.
Figure 7.
Proposed CNN model. The batch dimension (number of samples in the dataset) is denoted as None, as it is not fixed.
Regarding the learning process, the model was trained for 100 epochs with minibatch gradient descent (40 examples per minibatch) [43], using the categorical cross-entropy error and Adam optimizer [51], which is widely used for deep learning tasks and highly recommended in the literature [43], [52], [53]. The working dataset was randomly divided into a training set (70%) and a test set (30%). The training set was used in this learning process and the test set was used to assess the performance of the model.
The tuning of all the model parameters mentioned above (convolutional filter size, subsampling mask size, number of fully connected layers, number of neurons in fully connected layers, number of epochs and minibatch size) is based on the testing of different configurations. As shown in Table 3 (3.2.1 Model tuning), the chosen configuration is the one that yielded the best results.
Table 3.
Performance results for different CNN model configurations, using random cross validation executed 5 times (we report the mean and standard deviation of all executions). Configuration parameters: K1, size of the convolutional filter; K2, size of the subsampling mask; K3, number of fully connected layers; K4, number of neurons in fully connected layers; K5, number of epochs; K6, size of the minibatch.
| Configuration ID | K1 | K2 | K3 | K4 | K5 | K6 | Test accuracy (%) | Number of parameters | Training time (s) |
|---|---|---|---|---|---|---|---|---|---|
| (1) | 600 | 4 | 1 | 20 | 100 | 40 | 98.43 (σ = 0.88) | 2968 | 16.38 (σ = 1.08) |
| (2) | 400 | 4 | 1 | 20 | 100 | 40 | 98.43 (σ = 1.47) | 3368 | 21.48 (σ = 0.54) |
| (3) | 750 | 4 | 1 | 20 | 100 | 40 | 98.04 (σ = 1.75) | 2658 | 7.65 (σ = 0.17) |
| (4) | 600 | 2 | 1 | 20 | 100 | 40 | 98.04 (σ = 2.15) | 3968 | 15.61 (σ = 0.46) |
| (5) | 600 | 11 | 1 | 20 | 100 | 40 | 97.25 (σ = 2.00) | 2328 | 17.67 (σ = 0.45) |
| (6) | 600 | 4 | 2 | 22 | 100 | 40 | 98.43 (σ = 1.92) | 3590 | 16.43 (σ = 0.45) |
| (7) | 600 | 4 | 3 | 10 | 100 | 40 | 96.86 (σ = 2.66) | 2608 | 15.60 (σ = 0.40) |
| (8) | 600 | 4 | 1 | 10 | 100 | 40 | 96.08 (σ = 5.95) | 2388 | 15.31 (σ = 0.70) |
| (9) | 600 | 4 | 1 | 32 | 100 | 40 | 97.65 (σ = 2.88) | 3664 | 15.93 (σ = 0.35) |
| (10) | 600 | 4 | 1 | 20 | 80 | 40 | 98.04 (σ = 1.24) | 2968 | 12.97 (σ = 0.81) |
| (11) | 600 | 4 | 1 | 20 | 120 | 40 | 98.43 (σ = 0.78) | 2968 | 18.28 (σ = 0.40) |
| (12) | 600 | 4 | 1 | 20 | 100 | 35 | 98.04 (σ = 1.24) | 2968 | 17.19 (σ = 0.47) |
| (13) | 600 | 4 | 1 | 20 | 100 | 60 | 96.86 (σ = 2.00) | 2968 | 14.83 (σ = 0.53) |
It should also be noted that this architecture has been implemented using Keras (with Tensorflow backend), which is an open source neural network library, widely used by the research community [54]. Hence, the proposed CNN model is described in Fig. 7 according to Keras/Tensorflow conventions.
3.2.1. Model tuning
The architecture of the proposed CNN model is defined by the size of the convolutional filter (), the size of the subsampling mask (), the number of fully connected layers (), the number of neurons in fully connected layers (), the number of epochs () and the size of the minibatch (). As shown in Table 3, we tested several configurations and chose the one that achieved the highest accuracy: (1). Although (2,6,11) configurations also yielded good results, they were discarded, as they led to more complex models, which required a greater number of parameters to be tuned and more time to complete the training.
4. Results
The purpose of the proposed system is to determine the operating condition of the machine on the basis of raw machine operating data. To this end, the CNN model extracts the relevant features from the data and performs the classification on them. The results of the classification and the features learned by the model are presented below.
4.1. Classification results
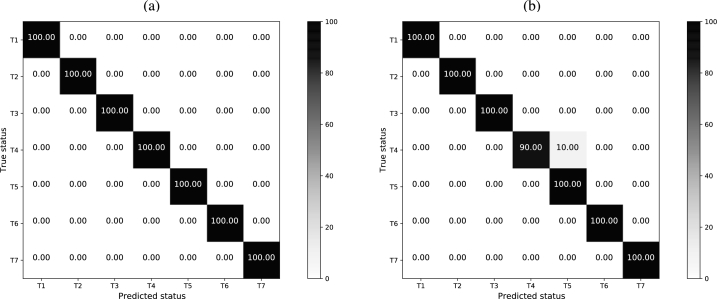
Fig. 8 shows the results of the classification in terms of the confusion matrix. Here we can see that the model determines the operating condition of the machine with a 100% accuracy for all classes in the training set, as well as in the test set, except for T4 class, where the rate drops to 90%. Therefore, the model achieves an accuracy of 100% in the training set and of 98% in the test set. Using different training and test sets, the average performance of the model is of 100.00% () accuracy in the training set and of 98.43% () in the test set, as we see in Table 4. In view of these results, we can assert that the proposed model solves the classification with a great performance.
Figure 8.
Confusion matrix of the machine condition classification using the proposed CNN model. (a) Results on the training set. (b) Results on the test set.
Table 4.
Performance results of the CNN model compared to other conventional classifiers, using random cross validation executed 5 times (we report the mean and standard deviation of all executions).
| Accuracy (%)1 | Precision (%)1 | Recall (%)1 | f1-score (%)1 | Number of parameters2 | Computational performance |
||
|---|---|---|---|---|---|---|---|
| Train (s) | Test (ms) | ||||||
| Proposed CNN model | |||||||
| Multi-Layer Perceptron | |||||||
| SVC (linear) | |||||||
| SVC (polynomial) | |||||||
| SVC (RBF) | |||||||
| RFC | |||||||
Classification metrics in the test set. In the training set, the classifiers have achieved a score of 100.00% () in all metrics.
For the CNN model and the MLP it is the number of learnable parameters. For SVC's it is the number of coefficients. For the RFC it is the number of trees in the forest.
4.1.1. Comparison with feature engineering classifiers
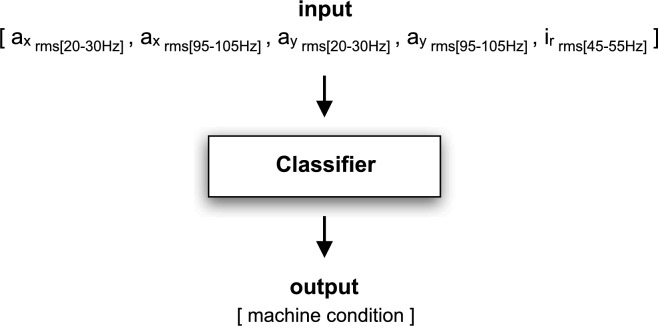
The performance of the model is compared with that of other classifiers based on manually engineered features. For this purpose, five representative features of the system have been extracted from data: rms value of and in the 20-30 Hz frequency band (1× machine rotational frequency, accounting for mechanical imbalances); rms value of and in the 95-105 Hz frequency band (2× machine supply frequency, regarding electrical imbalances); and rms value of in the 45-55 Hz frequency band (1× machine supply frequency, noting power supply imbalances). The classifiers proposed for comparison receive as input a vector with these five features and return as output the condition of the machine (Fig. 9).
Figure 9.
Working context of the classifiers proposed for comparison.
For an exhaustive comparison, several classifiers were used: (1) Multi-Layer Perceptron with 4 hidden layers of 20 neurons each; (2) SVC with linear kernel and penalty of the error term C = 1000; (3) SVC with polynomial kernel, degree = 3, C = 10 and kernel coefficient gamma = 10; (4) SVC with RBF kernel, C = 10 and gamma = 10; (5) RFC with max depth = 6. The performance of the CNN model and all of these classifiers is shown in Table 4, in terms of the following metrics:
-
•Accuracy (ratio of correctly predicted observations to the total observations), precision (ratio of correctly predicted positive observations to the total predicted positive observations), recall (ratio of correctly predicted positive observations to all observations in actual class) and f1-score (weighted average of precision and recall). These error measures can be calculated from the confusion matrix using the expressions (10)-(13), where: TP is the amount of true positive classifications, TN is the amount of true negative classifications, FP is the amount of false positive classifications and FN is the amount of false negative classifications.
(10) (11) (12) (13) -
•
Number of parameters in the model, as an indicator of the computational complexity of the model.
-
•
And finally, the model is also evaluated in terms of online and offline performance. For this purpose, two times are measured: the time the model takes to complete the training and the time it takes to classify an incoming sample.
As we see in Table 4, the CNN model achieves excellent results in all metrics derived from the confusion matrix: 98.43% accuracy, 98.40% precision, 98.40% recall and 98.40% f1-score. The table also shows that these results are comparable to those obtained using traditional classifiers. On the other hand, our model is the most complex, requiring a greater number of parameters to be tuned, and it is also the most computationally demanding, requiring more time both to complete the training and to classify an input sample.
However, the proposed CNN model proves to be able to classify the operating condition of the machine almost as successfully as conventional classifiers, even though it works in a less favourable context, without any machine information and learning by itself the relevant features to perform the classification. The consumption of resources, although the highest, is admissible and allows the machine to be monitored in real time.
4.1.2. Classification on a bearing fault dataset
As mentioned in Section 2.1, feature-engineered classifiers are highly problem-dependent and cannot be easily reused in new contexts. In order to assess the capability of the proposed system (feature-learning based) to monitor the condition of new machines, we evaluate its performance on another dataset [55]. It is a bearing fault dataset containing the radial vibration acceleration of a rotating machine, measured over three operating states along several conditions: 3 normal operation conditions at the same load, 10 outer race fault conditions at various loads and 7 inner race fault conditions at various loads (Table 5). We randomly take this data to build our training and test sets, following the assumption of considering 1 normal operation, 3 outer race fault and 2 inner race fault conditions for the test set and the remaining conditions for the training set.
Table 5.
Bearing fault dataset.
| Machine condition | Scenario (load in lbs, number of samples) |
|---|---|
| Normal operation (N) | N1(270,292968), N2(270,292968), N3(270,292968) |
| Outer race fault (O) | O1(25,146484), O2(50,146484), O3(100,146484), O4(150,146484), O5(200,146484), O6(250,146484), O7(270,292968), O8(270,292968), O9(270,292968), 10(300,146484) |
| Inner race fault (I) | I1(0,146484), I2(50,146484), I3(100,146484), I4(150,146484), I5(200,146484), I6(250,146484), I7(300,146484) |
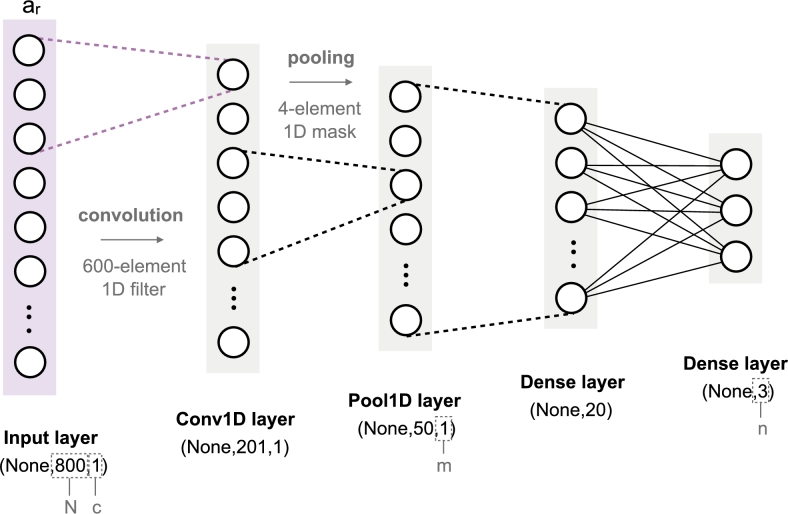
To test the system on this new data, we proceeded as described in Section 3: first, we normalized the dataset and used the windowing technique to pre-process the raw data; then, we trained the CNN model. This model has identical parameters (convolutional filter size, subsampling mask size, number of fully connected layers, number of neurons in fully connected layers, number of epochs and minibatch size) and similar architecture to that proposed in Section 3.2. The differences lie in the number of channels of the input layer ( instead of ) and the number of units of the output layer ( instead of ) (Fig. 10). The results of the classification are shown in Table 6 (B).
Figure 10.
CNN model adapted to the new dataset. The batch dimension (number of samples in the dataset) is denoted as None, as it is not fixed.
Table 6.
Performance results of the CNN model for the two datasets, using random cross validation executed 5 times (we report the mean and standard deviation of all executions).
| Accuracy (%)1 | Precision (%)1 | Recall (%)1 | f1-score (%)1 | |
|---|---|---|---|---|
| A) Original dataset | ||||
| (B) Bearing fault dataset [55] |
Classification metrics in the test set. In the training set, the CNN model has achieved a score of 100.00% () in all metrics.
Table 6 compares the classification of the two datasets used in this paper: (A) the original dataset, presented in Section 3.1 and based on which we designed the proposed system; (B) the new dataset, presented in this section. As we can see from the table, the system proves to be a good classifier in (B), although it is better in (A), which was expected, as the model parameters have been tuned to be used in (A). But it is remarkable the system's ability to classify the condition of a new rotating machine and to do so with high accuracy: 91.81% in the test set. In comparison, [56] proposes three classifiers (robust one-class SVM classifiers, feature engineering based) that achieve similar performance: 96%, 86% and 84% accuracy, considering as positive class the normal operation, the inner race fault and the outer race fault, respectively.
These results are evidence of the potential of feature learning, which in this case allows us to deal, using the same system, with two different machines and without the need for prior knowledge about them.
4.2. Feature learning results
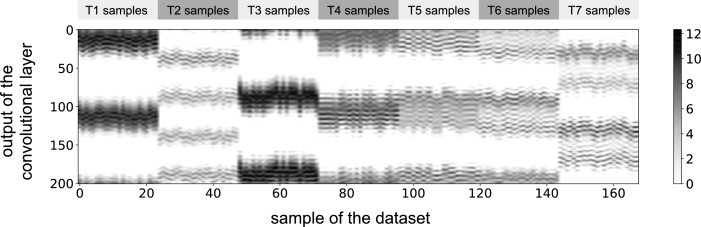
The convolutional layer of the model is tuned during the training phase in order to extract the relevant features from the input data. Fig. 11 shows the output vector of this layer for all samples in the dataset, where we can appreciate that vectors of each test present similar features. Therefore, the convolutional layer learns a representation of the input data that seems to help in discriminating the state of the rotating machine (it should be noted that the most confusing states appear to be T4/T5/T6, which is consistent with the confusion matrices in Fig. 8, where we see that the model confuses samples from tests T4/T5). This layer consists of a single 3-channel convolutional filter which is responsible for transforming input data into feature vectors. To that end, the filter learns to enhance the harmonics with more information to the classification task, and hence its frequency response contains valuable information about the machine.
Figure 11.
Output of the convolutional layer for each sample in the dataset.
Once the training is finished, the convolutional filter is defined by three weight vectors, whose frequency representation reveals the features learned by the model. To transfer these weight vectors to the frequency domain, we use the FFT (Fast Fourier Transform) (14), where represents the vector of weights and is the size of the filter (). According to this approach, we plot in Fig. 12 the frequency response of the filter learned by the CNN model, where each weight vector is related to a different input channel: (horizontal acceleration), (vertical acceleration) and (phase R current).
| (14) |
Figure 12.
Frequency response of the convolutional filter learned by the proposed CNN model: (a) ir channel, (b) ax channel, (c) ay channel.
This convolutional filter extracts the frequencies that are relevant to the classification task. Therefore, the weight vectors contain a great deal of information about the monitored machine and their analysis makes it possible to deduce constructional and operative parameters of the machine, as detailed below:
-
•
In the channel (Fig. 13) we can identify the power supply frequency of the machine, which is the fundamental frequency of the filter. This shows that the CNN coherently identified the fundamental frequency as a relevant feature in discriminating the condition of the machine. We also observe harmonics of this frequency at and .
-
•
In the channel (Fig. 14) the power supply frequency is present again , as well as other frequencies, such as the ball pass frequency of the outer race or the rotational speed of the machine . They appear together in the shaded area in the figure, where there is a high-frequency modulation with sidebands, being the distance between the two carrier frequencies.
-
•
In the channel (Fig. 15) we can see the frequencies already mentioned () and the ball pass frequency of the inner race , which is present at both low and high frequency.
Figure 13.
Analysis of the ir channel of the convolutional filter.
Figure 14.
Analysis of the ax channel of the convolutional filter.
Figure 15.
Analysis of the ay channel of the convolutional filter.
In short, the analysis of the convolutional filter concludes that: Hz, Hz, Hz and Hz. Therefore, the study of the features learned by the model provides a priori unknown information of the machine. Furthermore, on the basis of these operational parameters, it would be possible to deduce constructional parameters of the machine, such as the number of balls in the bearings (n) or the ratio between ball and pitch diameters . Using the expressions (4)-(7) we obtain a number of eight balls in the bearings and a diameter ratio of 0.25 , both of which match reality, as shown in Fig. 16.
Figure 16.
Bearing geometry of the testing machine.
5. Conclusion
In this paper, we propose a CNN model for detection and diagnosis of faults in rotating machines, which classifies the state of the machine on the basis of raw machine operating data. This approach integrates the two blocks of traditional fault detection into a single learning body: feature extraction and classification. The model has the ability to learn the best representation of the input data (it learns to extract the optimal features) to perform the classification. This means a high level of generalization and eliminates the need for feature engineering, so no experience or prior knowledge of the machine is required.
The proposed system has been tested on vibration and current operating data of a rotating machine with seven possible states, comparing its performance with that of other classifiers based on manually engineered features (Multi-Layer Perceptron, Support Vector Classifier, Random Forest Classifier). The results indicate that our CNN model is capable of determining the condition of the machine with an accuracy of 98%, almost as accurately as conventional classifiers. Furthermore, the analysis of the features learned by the model reveals operative and constructional parameters of the machine, such as its rotational speed or the number of balls in the bearings. It can therefore be concluded that the proposed CNN model not only successfully classifies the operating condition without the need for prior knowledge of the machine, but also provides us with unknown information about it. Finally, the proposed system has also reported good classification performance on a bearing fault dataset from another machine, thus demonstrating it can be successfully used in the monitoring of other rotating machines.
In view of these good results, we will keep exploring the potential of deep convolutional neural networks, with particular emphasis on the analysis of the features learned by the convolutional layers. On that topic, we have experimentally shown in this paper that the optimal solutions to the classification problem result in convolutional filters whose frequency responses reflect the relevance of the harmonics that contain more information for the classification task. Here we have proposed a model with one convolutional layer containing one convolutional filter, which extracts high level features, of easy interpretation. In deeper and more complex CNN models, with a greater number of convolutional layers and filters per layer, the learned features conform a compositional hierarchy and their interpretation may become harder. The impact of the deep model architecture on the interpretability of the learned features is not an obvious question. It is an open problem, which will be the topic of our future work.
Declarations
Author contribution statement
Ana González-Muñiz: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Ignacio Díaz & Abel A. Cuadrado: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This work was supported by the Spanish Ministry of Economy (MINECO) & FEDER funds from the EU (under grant DPI2015-69891-C2-1/2-R). This work was also supported by the Principado de Asturias government through the predoctoral grant “Severo Ochoa”.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Mobley R.K. Elsevier; 2002. An Introduction to Predictive Maintenance. [Google Scholar]
- 2.Graney B.P., Starry K. Rolling element bearing analysis. Mater. Eval. 2012;70(1):78–85. [Google Scholar]
- 3.Nandi S., Toliyat H.A. Industry Applications Conference, 1999. Thirty-Fourth IAS Annual Meeting. Conference Record of the 1999 IEEE, Vol. 1. IEEE; 1999. Condition monitoring and fault diagnosis of electrical machines-a review; pp. 197–204. [Google Scholar]
- 4.Poyhonen S., Jover P., Hyotyniemi H. Control, Communications and Signal Processing, 2004. First International Symposium on. IEEE; 2004. Signal processing of vibrations for condition monitoring of an induction motor; pp. 499–502. [Google Scholar]
- 5.Tavner P. Review of condition monitoring of rotating electrical machines. IET Electr. Power Appl. 2008;2(4):215–247. [Google Scholar]
- 6.Lacey S. An overview of bearing vibration analysis. Maint. Asset Manag. 2008;23(6):32–42. [Google Scholar]
- 7.Al-Badour F., Sunar M., Cheded L. Vibration analysis of rotating machinery using time–frequency analysis and wavelet techniques. Mech. Syst. Signal Process. 2011;25(6):2083–2101. [Google Scholar]
- 8.Smith W.A., Randall R.B. Rolling element bearing diagnostics using the case western reserve university data: a benchmark study. Mech. Syst. Signal Process. 2015;64:100–131. [Google Scholar]
- 9.Boškoski P., Petrovčič J., Musizza B., Juričić D. Detection of lubrication starved bearings in electrical motors by means of vibration analysis. Tribol. Int. 2010;43(9):1683–1692. [Google Scholar]
- 10.Yan R., Gao R.X., Chen X. Wavelets for fault diagnosis of rotary machines: a review with applications. Signal Process. 2014;96:1–15. [Google Scholar]
- 11.Konar P., Chattopadhyay P. Bearing fault detection of induction motor using wavelet and support vector machines (svms) Appl. Soft Comput. 2011;11(6):4203–4211. [Google Scholar]
- 12.Li B., Zhang P.-l., Liu D.-s., Mi S.-s., Ren G.-q., Tian H. Feature extraction for rolling element bearing fault diagnosis utilizing generalized s transform and two-dimensional non-negative matrix factorization. J. Sound Vib. 2011;330(10):2388–2399. [Google Scholar]
- 13.Liu X., Ma L., Mathew J. Machinery fault diagnosis based on fuzzy measure and fuzzy integral data fusion techniques. Mech. Syst. Signal Process. 2009;23(3):690–700. [Google Scholar]
- 14.LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521(7553):436. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 15.Tipping M.E., Bishop C.M. Probabilistic principal component analysis. J. R. Stat. Soc., Ser. B, Stat. Methodol. 1999;61(3):611–622. [Google Scholar]
- 16.Olshausen B.A., Field D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381(6583):607. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- 17.Neal R.M. Connectionist learning of belief networks. Artif. Intell. 1992;56(1):71–113. [Google Scholar]
- 18.Hinton G.E., Zemel R.S. Advances in Neural Information Processing Systems. 1994. Autoencoders, minimum description length and Helmholtz free energy; pp. 3–10. [Google Scholar]
- 19.Bengio Y., Courville A., Vincent P. Representation learning: a review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013;35(8):1798–1828. doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- 20.Li B., Chow M.-Y., Tipsuwan Y., Hung J.C. Neural-network-based motor rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2000;47(5):1060–1069. [Google Scholar]
- 21.Kowalski C.T., Orlowska-Kowalska T. Neural networks application for induction motor faults diagnosis. Math. Comput. Simul. 2003;63(3–5):435–448. [Google Scholar]
- 22.Bin G., Gao J., Li X., Dhillon B. Early fault diagnosis of rotating machinery based on wavelet packets—empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012;27:696–711. [Google Scholar]
- 23.AlThobiani F., Ball A. An approach to fault diagnosis of reciprocating compressor valves using Teager–Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014;41(9):4113–4122. [Google Scholar]
- 24.Jia F., Lei Y., Lin J., Zhou X., Lu N. Deep neural networks: a promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016;72:303–315. [Google Scholar]
- 25.Gan M., Wang C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings. Mech. Syst. Signal Process. 2016;72:92–104. [Google Scholar]
- 26.LeCun Y., Bengio Y. Convolutional networks for images, speech, and time series. Handbook Brain Theory Neural Netw. 1995;3361(10):1995. [Google Scholar]
- 27.Sainath T.N., Mohamed A.-r., Kingsbury B., Ramabhadran B. Acoustics, Speech and Signal Processing (ICASSP), 2013 IEEE International Conference on. IEEE; 2013. Deep convolutional neural networks for lvcsr; pp. 8614–8618. [Google Scholar]
- 28.Krizhevsky A., Sutskever I., Hinton G.E. Advances in Neural Information Processing Systems. 2012. Imagenet classification with deep convolutional neural networks; pp. 1097–1105. [Google Scholar]
- 29.Cireşan D.C., Meier U., Gambardella L.M., Schmidhuber J. Deep, big, simple neural nets for handwritten digit recognition. Neural Comput. 2010;22(12):3207–3220. doi: 10.1162/NECO_a_00052. [DOI] [PubMed] [Google Scholar]
- 30.Zhao R., Yan R., Chen Z., Mao K., Wang P., Gao R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019;115:213–237. [Google Scholar]
- 31.Jia F., Lei Y., Lu N., Xing S. Deep normalized convolutional neural network for imbalanced fault classification of machinery and its understanding via visualization. Mech. Syst. Signal Process. 2018;110:349–367. [Google Scholar]
- 32.Criminisi A., Shotton J., Konukoglu E. Decision forests: a unified framework for classification, regression, density estimation, manifold learning and semi-supervised learning. Found. Trends Comput. Graph. Vis. 2012;7(2–3):81–227. [Google Scholar]
- 33.Hsu C.-W., Lin C.-J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002;13(2):415–425. doi: 10.1109/72.991427. [DOI] [PubMed] [Google Scholar]
- 34.Devaney M.J., Eren L. Detecting motor bearing faults. IEEE Instrum. Meas. Mag. 2004;7(4):30–50. [Google Scholar]
- 35.Mierswa I., Morik K. Automatic feature extraction for classifying audio data. Mach. Learn. 2005;58(2–3):127–149. [Google Scholar]
- 36.Gupta P., Pradhan M. Fault detection analysis in rolling element bearing: a review. Mater. Today Proc. 2017;4(2):2085–2094. [Google Scholar]
- 37.Heng R., Nor M.J.M. Statistical analysis of sound and vibration signals for monitoring rolling element bearing condition. Appl. Acoust. 1998;53(1–3):211–226. [Google Scholar]
- 38.Randall R.B., Antoni J. Rolling element bearing diagnostics—a tutorial. Mech. Syst. Signal Process. 2011;25(2):485–520. [Google Scholar]
- 39.Saimurugan M., Ramachandran K., Sugumaran V., Sakthivel N. Multi component fault diagnosis of rotational mechanical system based on decision tree and support vector machine. Expert Syst. Appl. 2011;38(4):3819–3826. [Google Scholar]
- 40.Yang B.-S., Di X., Han T. Random forests classifier for machine fault diagnosis. J. Mech. Sci. Technol. 2008;22(9):1716–1725. [Google Scholar]
- 41.Kankar P.K., Sharma S.C., Harsha S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011;38(3):1876–1886. [Google Scholar]
- 42.Bishop C.M. Oxford University Press; 1995. Neural Networks for Pattern Recognition. [Google Scholar]
- 43.Ruder S. An overview of gradient descent optimization algorithms. arXiv:1609.04747 arXiv preprint.
- 44.Rumelhart D.E., Hinton G.E., Williams R.J. Learning representations by back-propagating errors. Nature. 1986;323(6088):533. [Google Scholar]
- 45.Dumoulin V., Visin F. A guide to convolution arithmetic for deep learning. arXiv:1603.07285 arXiv preprint.
- 46.Boureau Y.-L., Ponce J., LeCun Y. Proceedings of the 27th International Conference on Machine Learning (ICML-10) 2010. A theoretical analysis of feature pooling in visual recognition; pp. 111–118. [Google Scholar]
- 47.Hahnloser R.H., Sarpeshkar R., Mahowald M.A., Douglas R.J., Seung H.S. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature. 2000;405(6789):947. doi: 10.1038/35016072. [DOI] [PubMed] [Google Scholar]
- 48.Glorot X., Bordes A., Bengio Y. Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics. 2011. Deep sparse rectifier neural networks; pp. 315–323. [Google Scholar]
- 49.Patterson J., Gibson A. O'Reilly Media, Inc.; 2017. Deep Learning: A Practitioner's Approach. [Google Scholar]
- 50.LeCun Y.A., Bottou L., Orr G.B., Müller K.-R. Neural Networks: Tricks of the Trade. Springer; 2012. Efficient backprop; pp. 9–48. [Google Scholar]
- 51.Kingma D.P., Ba Adam J. A method for stochastic optimization. arXiv:1412.6980 arXiv preprint.
- 52.Gregor K., Danihelka I., Graves A., Rezende D.J., Wierstra D. Draw: a recurrent neural network for image generation. arXiv:1502.04623 arXiv preprint.
- 53.Xu K., Ba J., Kiros R., Cho K., Courville A., Salakhudinov R., Zemel R., Bengio Y. International Conference on Machine Learning. 2015. Show, attend and tell: neural image caption generation with visual attention; pp. 2048–2057. [Google Scholar]
- 54.Chollet F. Keras. 2015. https://keras.io
- 55.Bechhoefer E. Condition based maintenance fault database for testing of diagnostic and prognostics algorithms. 2013. https://mfpt.org/fault-data-sets/
- 56.Prayoonpitak T., Wongsa S. A robust one-class support vector machine using Gaussian-based penalty factor and its application to fault detection. Int. J. Mater. Mech. Manuf. 2017;5(3):146–152. [Google Scholar]