Abstract
Objective
Deleterious impact loading to cartilage initiates post-traumatic osteoarthritis (OA). While cytokine and enzyme levels regulate disease progression, specific mechanical cues that elucidate cellular OA origins merit further investigation. We defined the dominant pericellular and cellular strain/stress transfer mechanisms following bulk-tissue injury associated with cell death.
Method
Using an in vitro model, we investigated rate-dependent loading and spatial localization of cell viability in acute indentation and time-course studies. Atomic force microscopy (AFM) and magnetic resonance imaging (MRI) confirmed depth-wise changes in cartilage micro/macro-mechanics and structure post-indentation. To understand the transfer of loading to cartilage domains, we computationally modeled full-field strain and stress measures in interstitial matrix, pericellular and cellular regions.
Results
Chondrocyte viability decreased following rapid impact (80 %/sec) versus slow loading (0.1 %/sec) or unloaded controls. Viability was lost immediately during impact within regions near the indenter-tissue contact but did not change over seven days of tissue culture. AFM studies revealed a loss of stiffness following 80 %/sec loading, and MRI studies confirmed an increased tensile and shear strain, but not relaxometry. Image-based patterns of chondrocyte viability closely matched computational estimates of amplified maximum principal and shear strain in interstitial matrix, pericellular and cellular regions.
Conclusion
Rapid indentation worsens chondrocyte death and degrades cartilage matrix stiffness in indentation regions. Cell death at high strain rates may be driven by elevated tensile strains, but not matrix stress. Strain amplification beyond critical thresholds in the pericellular matrix and cells may define a point of origin for early damage in post-traumatic OA.
Keywords: Osteoarthritis, Indentation Probing, Chondrocyte Viability, Tissue Mechanics, Confocal Microscopy, Atomic Force Microscopy (AFM), Finite Element Modeling (FEM)
INTRODUCTION
Articular cartilage consists of the thin and poro-viscoelastic soft tissue that provides a compliant, wear-resistant, and lubricious surface for smooth joint articulation. Traumatic injury subjects cartilage to excessive mechanical loading [1] and initiates a progressive degenerative cascade characteristic of post-traumatic osteoarthritis (OA) [2–6]. Single injurious indentation on young bovine cartilage decreased synthesis rates of molecules in the interstitial extracellular matrix (ECM), reduced chondrocyte viability, and compromised tissue-scale biomechanics [7–9]; however, mechanisms underlying these tissue responses remain largely unknown. Understanding how the physiological and biomechanical changes of the chondrocytes, surrounding pericellular matrix (PCM), and dense ECM deviate after single acute impact overloads will clarify the pathophysiology of OA.
Indentation of cartilage at high loading magnitudes and rates leads to matrix damage and cell death. Compression of bovine articular cartilage samples to 50% thickness induced macro cracks and fissures in the matrix [10]. Compression of cartilage to lower magnitudes (e.g., 30%) lead to cell death under sufficiently high strain rates [11]. Furthermore, indentation of cartilage to 50% thickness at 2.5 %/sec revealed no macro fissures or cracks, while increasing the strain rate to 12.5 %/sec lead to the appearance of surface cracks. These results agree with an in vitro cartilage and meniscus study where peak forces and stresses increased with strain rate [12]. Moreover, rapid indentation even at low impact energies can give rise to small microcracks in the collagen matrix [13]. High strain rates are also associated with matrix mechanical failure and cell deactivation [10]. Localized impact was additionally correlated to chondrocyte death at a threshold strain within 2 hours of impact [14]. To better understand the poro-viscoelastic, strain-rate-dependent behavior of articular cartilage, a careful comparison of slow (e.g. quasi-static) and impact strain rates that induce significant disparate tissue abnormalities merits investigation.
In previous injurious compression studies conducted on bovine articular cartilage explants, the affected chondrocytes demonstrated significant changes in their metabolic activity and synthesis of matrix molecules and factors. Specifically, protein synthesis of matrix-degrading proteins increased once cartilage explants were exposed to mechanical overloading [8, 9]. Twenty-four hours after a single injurious compression of bovine articular cartilage explants, the production of MMP-1, −3, −9, −13, ADAMTS-4, −5 and TIMP-1 increased by 4- to 250-fold. Such synthesis dynamics indicate that surviving chondrocytes release proteinases and related factors that further degrade the cartilage matrix.
The objective of our paper was to define the dominant pericellular and cellular strain/stress transfer mechanisms that lead to cell death following bulk-tissue injury. To better identify the multifactorial threshold that minimizes matrix mechanical failure along with chondrocyte viability, we chose a 40% strain magnitude and slow (0.1 %/sec) or rapid (80 %/sec) strain rates. We further sought to characterize the time-dependent progression of cell viability using in vitro bovine articular cartilage cylindrical explants after acute impact loading over a seven-day period. We characterized the damage progression after indentation, quantified by regional tissue biomechanics measures, including atomic force microscopy and magnetic resonance imaging. Multi-scale computational modeling allowed us to visualize spatial patterns of stress and strain measures in cartilage regions during indentation by using experimentally-derived boundary conditions and mechanical loading outcomes.
MATERIALS AND METHODS
Osteochondral Sample Culture
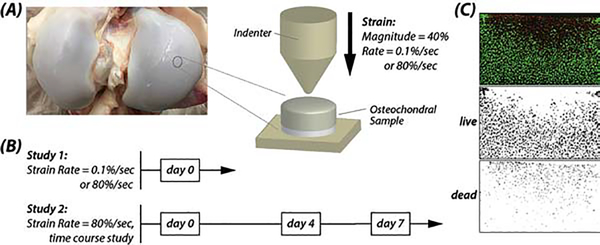
One bovine knees age ~6 months) were obtained from each of 17 animals within 48 hours of slaughter, and osteochondral cylindrical explant samples (radius = ~4.3 mm) were harvested aseptically (Figure 1). Multiple samples were obtained from the anterior loading regions of the femoral medial and lateral condyles (i.e., up to six samples per region), where cartilage shows a consistent pattern of structure and cell responses [15]. Importantly, this sampling scheme enabled acquisition of data from many assays while maintaining replication in each assay at the level of the animal/knee joint. Samples were rinsed 2–3 times in sterile 1× phosphate-buffered saline (PBS), and cartilage (1.5 mm thickness) was separated from the subchondral bone via a cutting apparatus jig. Samples were assigned to two separate studies that specifically investigated the influence of (0.1 or 80 %/sec) strain rate (N=6 knees), or acute impact loading followed by time-course incubation (N=11 knees) (Figure 1B). Samples were then cultured in 2–3 mL of 37 °C Dulbecco’s Modified Eagle’s Medium (DMEM) with 10% fetal bovine serum (FBS), 1% Penicillin/Streptomycin (P/S) and 1% bovine serum albumin (BSA), with the nutrient medium changed every two days.
Figure 1. Indentation testing assessed cellular viability and multiscale tissue mechanics in explanted cartilage.
Osteochondral samples were harvested from medial and lateral femoral condyles of bovine articular cartilage (A) and indented at controlled strain rates and magnitude, followed by transfer to a chemically-defined medium for time-course studies (B). Samples were indented with a 1 mm radius spherical indenter to a strain magnitude of 40 % at rates of 0.1 %/sec and 80 %/sec. (C) Chondrocyte viability was assessed by confocal microscopy and live/dead staining and quantified by ImageJ.
Indentation of Cartilage at High and Low Strain Rates
Samples were subjected to indentation using a bench-top mechanical test system (ElectroForce® 5500, TA Instruments, Eden Prairie, MN) and a steel hemispherical indenter (radius=1 mm). Prior to testing, the thickness of each sample (~2 mm, range: 1.6–2.3 mm) was measured with the indentation instrument to account for tissue swelling observed through culture duration. A tare load was applied (0.05 N), and then samples were indented in compression using a single-cycle triangle (compressive) waveform to 40% strain magnitude (determined from the thickness of the sample) applied to the articulating surface of the cartilage. The strain rate was controlled to 0.1 %/sec (slow) or 80 %/sec (rapid), and the force (200 N load cell; Futek) and displacement values over time were measured for each sample. After indentation, samples were either prepared for imaging or further cultured up to seven days.
Cell Viability
Chondrocyte viability was assessed via live/dead staining and confocal microscopy. Samples were submerged in a 3 mL solution of media containing 1 μM calcein-AM (calcein) and 3 μM propidium iodide (PI) (Thermo Fisher, Grand Island, NY). Stained samples were incubated at 37 °C for 15–20 minutes prior to imaging. For imaging, we utilized a 10× air objective, 1024×1024 pixels2 acquisition matrix, and excitation wavelengths of 543 nm (Texas Red) and 488 nm (Alexa Fluor). Images collected were analyzed with ImageJ (National Institutes of Health, Bethesda, MD), and viability was assessed using the percentage ratio of live/dead cells (Figure 1C). Images were thresholded, and live and dead cells were counted as objects with a minimum particle size of 13.5 and 9 squared pixels, and with a circularity of 0–1, respectively.
Local Measurement of Mechanical Properties by AFM
Micro-indentation tests by AFM allowed us to measure the local stiffness of the tissue after slow and fast indentation. Imaging was conducted using medial femoral condyle samples (N=6) that were prepared using a standard method by sectioning (30 μm thickness) with a vibratome [16]. Briefly, cartilage sections were washed thoroughly with PBS and pre-stained with calcein/PI to identify viable cells and placed into a PBS-filled liquid cell for AFM testing. A Keysight 5500 AFM system (Keysight Technologies Inc., Santa Rosa, CA) was combined with a Nikon Eclipse Ti wide-field inverted microscope (Nikon Instruments Inc., Melville, NY) to perform the microscale indentation, allowing for simultaneous AFM scanning and fluorescence microscopy. Image data were acquired on indentation locations and on the unaffected (unloaded, control) regions identified by calcein/PI stain. The AFM was operated in force-volume mode, wherein triplicate arrays (5×5) of force-distance (F-Z) curves were collected over the 30×30 μm2 scan area. The force trigger was set to 15 nN for all micro-indentations, which corresponded to an indentation depth of 0.4–2.2 μm, depending on the regional elasticity. To ensure a known geometry of the AFM probe, a cantilever with a borosilicate glass bead (~62 GPa Young’s modulus and 5 μm diameter) attached to the free end (NovaScan, Ames, IA) was used for all AFM tests. The cantilever stiffness was pre-calibrated to be 0.07 N/m by the thermal fluctuation method [17]. The Young’s moduli of were calculated based on Hertz theory of contact mechanics [18].
Local Measurement of Mechanics and Structure by MRI
Measurement of intra-tissue strain was obtained by MRI (dualMRI) using displacements under applied loading via compressive loading inside a 7T MRI scanner (Bruker Biospec, Billerica, MA) [19, 20]. Fast and slow loaded samples (N=3) were placed in the MRI-compatible bioreactor, immersed in PBS, and cyclically and intermittently loaded in unconfined compression (25 N with 600 cycles at 0.33 Hz) to reach a quasi-steady state load-deformation behavior with a hemisphere indenter. An MRI (DENSE-FISP) imaging sequence was used with a xyz displacement encoding gradient area of 1.13 π/mm. FISP imaging parameters were: TE/TR = 2.5/5.0 ms; in-plane spatial resolution = 250 × 250 μm2; image matrix size = 128 × 128 pixels2; number of averages = 8; slice thickness = 1.0 mm; and flip angle = 15o. Displacements and principal strains were obtained from phase contrast data using MATLAB (Mathworks, Natick, MA). For quantitative MRI assessment of tissue structure, T2 mapping was determined using a multislice, multiecho sequence, with parameters: TE = [11.5, 23.0, 34.5, 46.0, 57.5, 69.0, 80.5, 92.0] ms and TR = 1000 ms. Likewise, T1ρ mapping was determined with the following parameters: TE/TR = 50.3/2000 ms; spin-lock frequency = 851 Hz; and spin-lock durations of [10, 20, 40, 60, 80, 100, 120, 140, 160, 180] ms. Relaxation times were determined using a monoexponential curve-fitting algorithm in MATLAB. For each dualMRI strain map, a 6×9 pixel2 matrix was taken from the highest strain region (usually around the indenter location) to calculate the average strain. The averages were calculated over the entire sample for T2 and T1ρ maps (little spatial variation in the data was observed).
Bulk Measurement of Mechanical Properties During Impact
To characterize the biomechanics of the tissue from the force and displacement measurements during the indentation test, a MATLAB script was generated to calculate the stress-strain relation of the samples from the strain rate study. Calculations for (first Piola-Kirchhoff) stress assumed that the contact surface area of the spherical indenter remained in contact with the tissue and increased accordingly with the indenter’s displacement. A hysteresis stress-strain curve was generated, and the loading curve was isolated so an effective Young’s modulus could be calculated from a linear regression of the elastic region. The average slope of the linear regressions was used to estimate Young’s modulus for each strain rate.
Multiscale Estimate of Interstitial ECM, PCM, and Cellular Mechanics by Finite Element Modeling
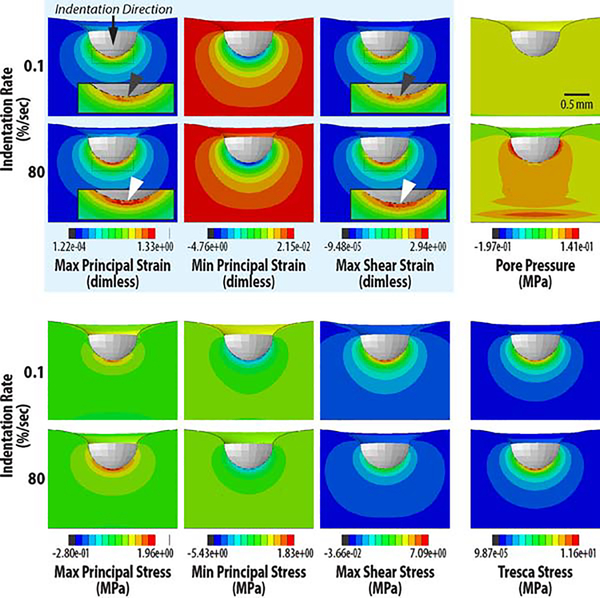
To estimate the local mechanical environment of the chondrocytes during indentation loading, we developed a multi-scale finite element model of the indentation test for both (0.1 %/sec and 80 %/sec) loading rates using ABAQUS 6.14 (Simulia, Providence, RI). First, a 3D model of the tissue was created using the average sample dimensions (4.3 × 2.04 mm2) and a mesh of C3D8P elements. The ECM was modeled using a poroelastic, neo-Hookean material model with density 1000kg/m3, Young’s Modulus 0.31 MPa, Poisson’s Ratio 0.42, and permeability 1.962E-8 mm/s, with void ratio 4 and specific weight of the wetting liquid 9.81E-6 [21]. To mimic experimental conditions, we fixed all displacement degrees of freedom for nodes on the bottom (glued) surface of the explant and set the corresponding fluid flux normal to this surface to zero. We then indented on the top surface using a rigid and impermeable spherical indenter of radius 1 mm. We specified all remaining nodes in contact with air as free to displace and set the corresponding fluid pressure to zero. The model included large deformation and was solved using the Soils procedure in ABAQUS. The distributions of potentially relevant mechanical parameters were plotted for spatial comparisons with the images of cell death, including pore pressure, max/min principal stresses, maximum shear stress, Tresca stress, max/min principal strains and maximum shear strain.
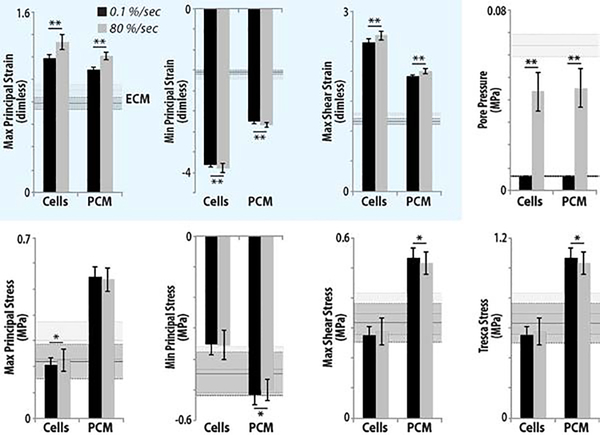
Second, to probe cellular responses, our 3D model was extended to include the ECM (i.e., interstitial matrix), PCM, and embedded chondrocytes within a conforming mesh [22]. The 3D model was designed to mimic the superficial zone directly underneath the indenter, and it was realized as a cube with fixed (100 μm) edge length that included 11 representative chondrocytes and their respective PCMs. This 3D model was also run under loading conditions for both the 0.1 and 80 % /sec loading rates and magnitudes. All elements were type C3D8P. Recognizing the wealth of data on the PCM [16, 23–26], we modeled this cartilage domain using a poroelastic and neo-Hookean material model with density 1000 kg/m3, Young’s modulus 0.0505 MPa, Poission’s Ratio 0.3, and permeability 1.962E-8 mm/s, with void ratio 4 and specific weight of the wetting liquid 9.81E-6 [27]. Likewise, chondrocytes were modeled using a poroelastic and neo-Hookean material model with density 1000 kg/m3, Young’s Modulus 0.01 MPa, Poisson’s Ratio 0.3, and permeability 9.81E-9 mm/s with void ratio 4 and specific weight of the wetting liquid 9.81E-6. We identified regions in the regions in ECM, PCM, and chondrocytes that represented the largest (10%; absolute) magnitudes of mechanical parameters and utilized these values for statistical analyses.
Statistical Analyses
Cell viability and MRI differences for samples tested at 0.1 and 80 %/sec strain rates were determined using one-way analysis of variance (ANOVA) (SAS Institute). AFM-based analysis of Young’s Modulus was performed using a two-way mixed model ANOVA, with strain rate and region location as fixed main effects and the strain rate × region interaction included in the model. To account for multiple measurements taken at each region, we included sample (nested within the strain rate × region interaction) as a random effect in this analysis. Time-course cell viability was analyzed using a two-way ANOVA, with the fixed effects of strain rate, time, and their interaction. Differences in cell, PCM, and ECM regions for samples tested at 0.1 and 80 %/sec strain rates were determined using two-way mixed model ANOVA. These models also included the strain rate × region interaction, and sample as a random effect. We evaluated the residuals of each model to confirm that our models met the statistical assumptions of ANOVA. Data are presented as mean ± 95% confidence interval, with p<0.05 considered statistically significant.
RESULTS
Strain Rate Study
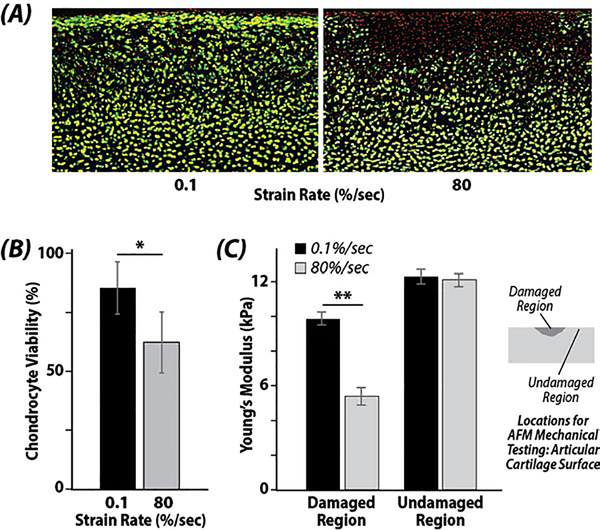
Chondrocyte viability decreased following rapid impact (80 %/sec) when compared to quasi-static loading (0.1 %/sec) or unloaded controls. A significant statistical difference was noted between the strain rates of 80 %/sec and 0.1 %/sec (p=0.0006). Chondrocyte viability decreased by 22% in 80 %/sec compared to 0.1 %/sec samples (Figure 2). AFM analysis revealed a loss of stiffness following 80 %/sec loading, and a significant statistical difference was noted between the indented region and the unaffected region of both strain rates (p=0.006) (Figure 2C).
Figure 2. High strain rates reduce cell viability and compromise local tissue biomechanics at the articular surface.
(A) Damaged regions and reduced cell viability (red signal, loss of green signal) are evident in regions impacted by the indenter at the (top) articular surface. (B) Chondrocyte viability was significantly reduced when the strain rate was increased from 0.1 %/sec to 80 %/sec (* p=0.0006). (C) Young’s modulus, as assessed by atomic force microscopy (AFM), was reduced in regions impacted by the indenter at high (80 %/sec) strain rates (damaged region) compared to regions that were not impacted (undamaged region) (** p=0.006).
Time-Course Damage Progression Study
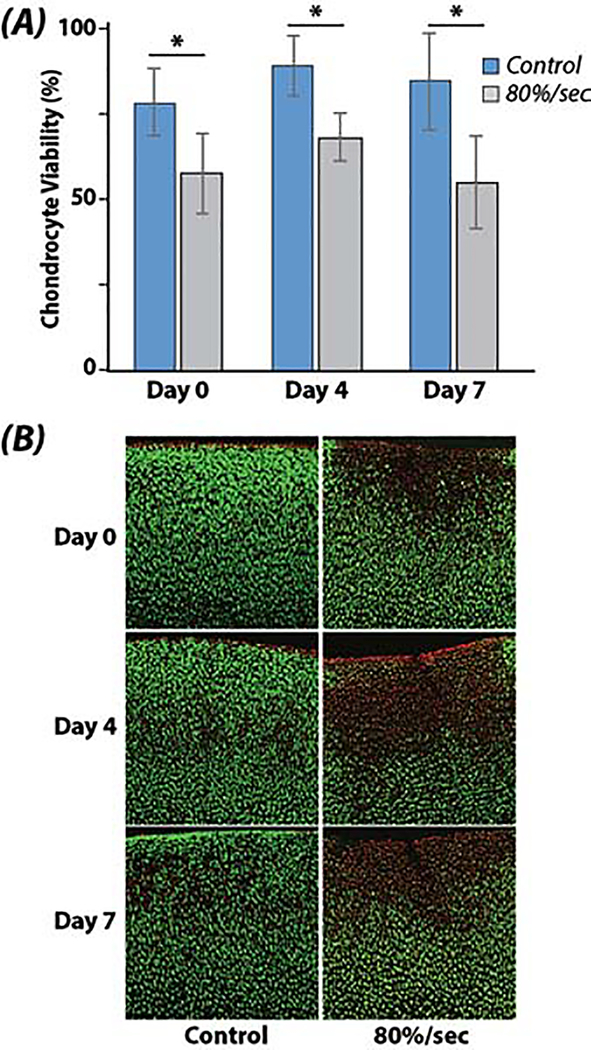
Viability was lost immediately during impact within the small region near the indenter-tissue contact, and was maintained over the culture duration (Figure 3). Indentation loading reduced chondrocyte viability by up to 30% at days 0, 4, and 7 following impact (p<0.001). Cell viability was marginally changed over the time duration compared to day 0 samples (p=0.034), however, this effect was influenced by changes at day 4 compared to day 0 (p=0.034), which returned to baseline levels by day 7 (p=0.928).
Figure 3. Chondrocyte viability remains unchanged following seven days of tissue culture.
(A) Cell viability is reduced in samples indented at high (80 %/sec) strain rates compared to unloaded controls. (B) Spatial loss of cell viability was still confined to the region impacted by the indenter after seven days, suggesting cell damage in this experimental model was driven primarily by acute, initial impact loading, and less so by secondary (e.g., cytokine, enzyme) damage mechanisms. (* p<0.001)
Structural Characterization by MRI
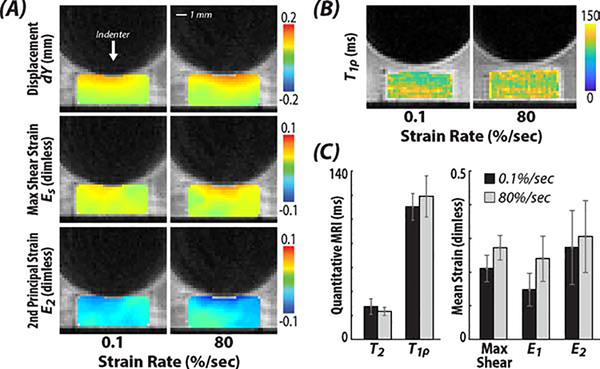
MRI studies showed trends of increased tensile and shear strain, but not relaxometry (Figure 3). DualMRI detected biomechanical changes between 0.1 %/sec and 80 %/sec strain rate indentations, with increased patterns of elevated maximum shear strain and principal strains under the same load-controlled compressive testing. The samples that experienced 80 %/sec strain rate indentation showed larger strains, though the changes were not statistically significant (p>0.05); the average maximum shear stain Es, and the 1st and 2nd principal strains E1 and E2, increased 29.5%, 62.1%, and 12.1% respectively. The mean values of the maximum shear strain, 1st and 2nd principal strains on samples experienced fast indentation were Es=0.027±0.004, E1=0.024±0.007 and E2=−0.031±0.011 respectively; while for the samples experienced slow indentation, Es=0.021±0.004, E1=0.015±0.005 and E2=−0.027±0.011. Samples that underwent 80 %/sec strain rate indentation also showed a 7.9% increase in T1ρ compared to those experienced 0.1 %/sec strain rate indentation, their average T2 was 14.6% lower, but these changes were not statistically significant (p>0.05).
Multiscale Computational Studies
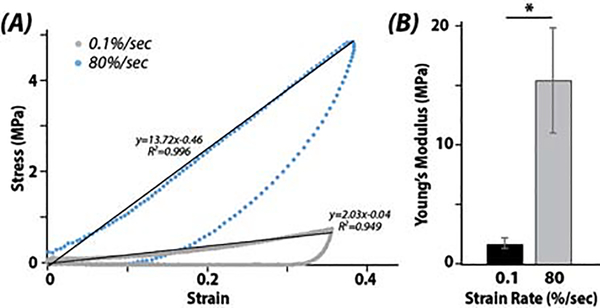
At matrix, pericellular, and cellular scales, image-based patterns of chondrocyte viability matched computational estimates of amplified strains. The calculated stress-strain relation hysteresis from the force and displacement measurements of the indentation test instrument demonstrated how cartilage responds dynamically to strain rate and was critical validation for our computational analysis. A significant difference between the stiffness measured in the linear regions per strain rate was noted (p<0.001) (Figure 5).
Figure 5. Increased stiffening and altered stress-strain responses were observed when explants were loaded at 80 %/sec compared to 0.1 %/sec strain rates.
Hysteresis curves (A) of the (first Piola-Kirchhoff) stress-strain during indentation and (B) corresponding elastic property data. (* p<0.001)
Image-based patterns of chondrocyte viability closely matched computational estimates of maximum principal strain and shear strain, but not interstitial pore pressure or shear stress, suggesting that principal strain alone may be responsible for cell death at high strain rates (Figure 6). We found significant differences in strain and pore pressure of the PCM and Cells between loading rates (p<0.001) (Figure 7), with amplified strain magnitudes observed at the cellular scale compared to ECM strain magnitudes. No significant differences were found in stress values due to impact (p>0.05).
Figure 6. Indentation at high strain rate leads to increased principal and shear strain patterns that match observed patterns of cell death.
Full-field mechanical quantities were computed through the cross section of cartilage in silico, and used to identify quantities within the tissue and beneath the indenter that were amplified during rapid (80 %/sec) loading compared to slow (0.1 %/sec) loading, i.e., similar to cell viability data. Mechanical quantities were largely unchanged due to loading rate, except for pore pressure (throughout the interior) and maximum principal and shear strain (white arrows) that were increased in magnitude at the cartilage-indenter interface at rapid (white arrows) compared to slow (dark grey arrows) loading.
Figure 7. Strain is amplified in the interstitial extracellular matrix, pericellular matrix, and cellular (Cells) regions in samples following rapid (80 %/sec) compared to slow (0.1 %/sec) strain rate loading.
Pore pressure was also increased in ECM, PCM, and cells, however, patterns of pressure did not match cell viability. In contrast, maximum principal and shear strains were amplified at each level, and there was a qualitative similarity between computational outcomes and patterns of cell viability. With the exception of the pore pressure, stress values were less influenced by strain rate at each spatial scale. (* p<0.05; ** p<0.0001)
DISCUSSION
This investigation quantified and assessed the effects of indentation tests in vitro on chondrocyte viability and tissue biomechanics of young bovine articular cartilage across a range of clinically applicable (slow to impact) strain rates. No progressive chondrocyte death was observed over seven-days, and chondrocyte viability decreased as strain rate increased. These results suggest that cell viability in this model system is driven by an initial, acute damage response that remains unchanged due to possible (e.g., cytokine, enzyme) effects that could influence the cell response as a secondary damage mechanism. We cannot exclude the possibility of secondary damage effects beyond the duration of our time course analysis (7 days), or in model systems that differ from our in vitro conditions.
The strain rate dependence of cell viability directly suggests a loading threshold for the initiation of excessive chondrocyte death. Interestingly, peak forces (and stresses) in this study ranged from 4–39 N (1–8 MPa) for the strain rate of 80 %/sec and from 2–6 N (0.4–1.2 MPa) for the strain rate of 0.1 %/sec. The loss of matrix structure and the possibility of microcrack formation was suggested by data following 80 %/sec indentation (Figure 2C). These findings are supported by the literature, with significant matrix damage arising beyond a impact threshold [7] that is minimized during quasi-static loading. Additionally, a critical and recent study also directly identified strain thresholds that impact chondrocyte death, and the probability of cell death that is strongly correlated strain norm [14], which aligns with the results presented herein.
The evaluated micro-mechanical Young’s moduli demonstrate how articular cartilage responds dynamically to mechanical stimuli at the micron-scale. After indentation, AFM imaging characterized a 900 μm2 area of the indented area and of the unaffected area. Correspondingly, an 80 %/sec strain rate induced a reduction of ~6.8 kPa on tissue stiffness, and the slow strain rate induced a reduction of ~2.4 kPa. It must be noted that these calculated values differ by a factor of almost a thousand with the macro-mechanical calculated Young’s moduli, which is consistent with known scale effects experimentally observed in cartilage [28–30]. Correspondingly, previous studies have shown that cell stiffness ranges in kPa, cartilage in MPa, and collagen in GPa [31–33]. This suggests that the AFM evaluated stiffness at the cellular or local matrix scale, with lower stiffness measured following loading at the 80 %/sec strain rate.
The evaluated macro-mechanical Young’s moduli demonstrate the poro-viscoelastic nature of bovine articular cartilage. Specifically, at 0.1 %/sec articular cartilage exhibits a more viscous dissipation that allows the tissue to deform to the indentation without significant viability changes; however, tissue softening still occurs. The poro-viscoelastic nature of articular cartilage depends on the structural components in articular cartilage that include water diffusion, proteoglycans, and type II collagen [34]. These components classify articular cartilage as a multiphase medium with two phases: a fluid phase and a solid phase. Since cartilage is predominantly composed of water, contact forces induce high interstitial fluid pressures that cause fluid to flow out of the ECM. Due to the porous structure of the ECM, its permeability controls the rate at which fluid pressure can be relieved during mechanical loading, and faster loading induces more resistance and thus apparent stiffness of the tissue under compression. This can be seen in our results, since the 0.1 %/sec strain rate appears to be softer than the 80 %/sec by almost a factor of 10. It must be noted that the time duration to reach a 40% strain magnitude was 0.5 seconds and 400 seconds for 80 %/sec and 0.1 %/sec, respectively.
Changes of mechanical properties of the tissue matrix were supported by dualMRI strain maps, as strains were increased on the samples experienced fast indentation indicating matrix degeneration and softening. Our intra-tissue analysis supports regional patterns of altered strain visualized by finite element analysis. The MRI data further suggested larger matrix softening at higher strain rate, as structural elements (e.g., collagen) would be unable to support loading following damage. We noted the decreased ability of standard MRI relaxometry to detect matrix damage, however trends the data support the possibility that increased sample sizes would enable robust quantification of differences between treatment groups at the population level.
By comparing the results of the FE model against cell viability, the spatial pattern of cell death at the cartilage-indentor interface qualitatively matched the pattern of maximum principal strain and shear strain in both loading conditions. This results supports the idea that the maximum principal and shear strain experienced at the bulk tissue level influences chondrocyte death. It may seem inconsistent that strain drives cell death, since both the slow and fast strain-rate compressions undergo the same applied displacement, and thus the same compressive strain at the macro or bulk scale. However, under fast strain-rate compression, the bulk tissue must deform isochorically as there is no time for significant fluid transport, and thus the lateral strains must be larger relative to the slow strain rate loading. In slow strain-rate compression fluid transport reduces the fluid volume fraction, lowers the effective bulk Poisson’s ratio, and reduces the lateral strains. Consequently, rapid loading in cartilage at the indentor-tissue interface can lead to excessive local strains that transfer across scale to impact cells.
Within the FE models, maximum principal strain and maximum shear strain is transferred across scale and region, directly influencing the strain observed in the pericellular matrix, and importantly, in cellular regions. In contrast, stress was elevated with rapid (80 %/sec) strain rate loading. Moreover, interstitial pore pressure appeared to vary the greatest between the two loading conditions with the pressure being significantly higher during the faster loading condition. However, distributions of interstitial pore pressure within cartilage do not match patterns of cell viability observed in this study. The pore pressure of the tissue is a time-dependent response to loading rate [35]. We attribute this to the tissue, and subsequently the chondrocytes, ability to resist the fast strain rate with interstitial fluid within the tissue. Intermittent bouts of hydrostatic pressure loading have been found to result in chondrocyte metabolism and apoptosis [36]. We found that the pore pressure of the chondrocytes also increased with a faster loading rate, possibly correlating cell death with this condition, albeit with patterns that remain inconsistent with cell viability.
Results of the present study implicate that indentation probing allows for the characterization of biomechanical properties of articular cartilage, along with assessing the correlation between strain rate and strain magnitude on chondrocyte viability. Chondrocyte viability decreased in the cartilage regions immediately under the indentation in tissue samples compressed at 80 %/sec versus 0.1 %/sec. Notably, damage propagation over seven days did not occur in samples exposed to 80 %/sec indentation. As assessed from the force and displacement measurements generated from AFM measurements and the indentation test instrument, the poroelastic of cartilage behavior depends greatly on strain rate. This was observed after samples compressed to 80 %/sec demonstrated a significant decrease in stiffness when compared to 0.1 %/sec indentation. The decrease in micro- and macro-mechanical stiffness was ~4.6 KPa and ~12 MPa, respectively, suggesting that damage to the cartilage solid matrix (e.g., collagens, proteoglycans) may occur during rapid compression. Understanding the role of specific biomechanical and biochemical factors leading to cell death and matrix damage may lead to a better understanding of post-injury osteoarthritis.
Figure 4. Spatially-dependent (local) strains were increased near the tissue-indenter interface within cartilage following 80 %/sec strain rate indentations compared to the 0.1 %/sec indentations.
Representative dualMRI data of the (A) displacement along y-axis, i.e., the loading direction, maximum shear strain, and 2nd principle strain. (B-C) Additionally, the quantitative MRI parameter T1ρ, which assesses tissue structure, was unchanged in samples following loading.
ACKNOWLEDGEMENTS
Michael Drakopoulos, Anita Asuquo, Sarah Stadler, David McMillan, and funding from the NIH and NSF are gratefully acknowledged. This work was supported in part by NIH grants R01 AR063712 and R21 AR066230, and NSF grants 1662429 and 1349735.
Footnotes
CONFLICT OF INTEREST
None.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Buckwalter JA, Brown TD. Joint injury, repair, and remodeling: roles in post-traumatic osteoarthritis. Clinical Orthopaedics and Related Research® 2004; 423: 7–16. [PubMed] [Google Scholar]
- 2.Guilak F, Fermor B, Keefe FJ, Kraus VB, Olson SA, Pisetsky DS, et al. The role of biomechanics and inflammation in cartilage injury and repair. Clinical Orthopaedics and Related Research® 2004; 423: 17–26. [DOI] [PubMed] [Google Scholar]
- 3.Hashimoto S, Nishiyama T, Hayashi S, Fujishiro T, Takebe K, Kanzaki N, et al. Role of p53 in human chondrocyte apoptosis in response to shear strain. Arthritis & Rheumatism: Official Journal of the American College of Rheumatology 2009; 60: 2340–2349. [DOI] [PubMed] [Google Scholar]
- 4.Martin JA, Brown TD, Heiner AD, Buckwalter JA. Chondrocyte senescence, joint loading and osteoarthritis. Clinical Orthopaedics and Related Research® 2004; 427: S96–S103. [DOI] [PubMed] [Google Scholar]
- 5.Wilson W, van Burken C, van Donkelaar C, Buma P, van Rietbergen B, Huiskes R. Causes of mechanically induced collagen damage in articular cartilage. Journal of Orthopaedic Research 2006; 24: 220–228. [DOI] [PubMed] [Google Scholar]
- 6.Wilson W, Van Rietbergen B, Van Donkelaar C, Huiskes R. Pathways of load-induced cartilage damage causing cartilage degeneration in the knee after meniscectomy. Journal of biomechanics 2003; 36: 845–851. [DOI] [PubMed] [Google Scholar]
- 7.Hosseini S, Veldink M, Ito K, Van Donkelaar C. Is collagen fiber damage the cause of early softening in articular cartilage? Osteoarthritis and cartilage 2013; 21: 136–143. [DOI] [PubMed] [Google Scholar]
- 8.Lee J, Fitzgerald J, DiMicco M, Cheng D, Flannery C, Sandy J, et al. Co-culture of mechanically injured cartilage with joint capsule tissue alters chondrocyte expression patterns and increases ADAMTS5 production. Archives of biochemistry and biophysics 2009; 489: 118–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee JH, Fitzgerald JB, DiMicco MA, Grodzinsky AJ. Mechanical injury of cartilage explants causes specific time dependent changes in chondrocyte gene expression. Arthritis & Rheumatism: Official Journal of the American College of Rheumatology 2005; 52: 2386–2395. [DOI] [PubMed] [Google Scholar]
- 10.Quinn T, Allen R, Schalet B, Perumbuli P, Hunziker E. Matrix and cell injury due to subimpact loading of adult bovine articular cartilage explants: effects of strain rate and peak stress. Journal of orthopaedic research 2001; 19: 242–249. [DOI] [PubMed] [Google Scholar]
- 11.Bae W, Schumacher B, Sah R. Indentation probing of human articular cartilage: effect on chondrocyte viability. Osteoarthritis and cartilage 2007; 15: 9–18. [DOI] [PubMed] [Google Scholar]
- 12.Nishimuta JF, Levenston ME. Response of cartilage and meniscus tissue explants to in vitro compressive overload. Osteoarthritis and cartilage 2012; 20: 422–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kaleem B, Maier F, Drissi H, Pierce D. Low-energy impact of human cartilage: predictors for microcracking the network of collagen. Osteoarthritis and cartilage 2017; 25: 544–553. [DOI] [PubMed] [Google Scholar]
- 14.Bartell LR, Fortier LA, Bonassar LJ, Cohen I. Measuring microscale strain fields in articular cartilage during rapid impact reveals thresholds for chondrocyte death and a protective role for the superficial layer. Journal of biomechanics 2015; 48: 3440–3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Neu CP, Khalafi A, Komvopoulos K, Schmid TM, Reddi AH. Mechanotransduction of bovine articular cartilage superficial zone protein by transforming growth factor β signaling. Arthritis & Rheumatism: Official Journal of the American College of Rheumatology 2007; 56: 3706–3714. [DOI] [PubMed] [Google Scholar]
- 16.Xu X, Li Z, Cai L, Calve S, Neu CP. Mapping the nonreciprocal micromechanics of individual cells and the surrounding matrix within living tissues. Scientific reports 2016; 6: 24272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hutter JL, Bechhoefer J. Calibration of atomic-force microscope tips. Review of Scientific Instruments 1993; 64: 1868–1873. [Google Scholar]
- 18.Johnson KL, Kendall K, Roberts A. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 1971; 324: 301–313. [Google Scholar]
- 19.Chan DD, Cai L, Butz KD, Trippel SB, Nauman EA, Neu CP. In vivo articular cartilage deformation: noninvasive quantification of intratissue strain during joint contact in the human knee. Scientific reports 2016; 6: 19220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chan DD, Neu CP. Transient and microscale deformations and strains measured under exogenous loading by noninvasive magnetic resonance. PloS one 2012; 7: e33463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li L, Soulhat J, Buschmann M, Shirazi-Adl A. Nonlinear analysis of cartilage in unconfined ramp compression using a fibril reinforced poroelastic model. Clinical Biomechanics 1999; 14: 673–682. [DOI] [PubMed] [Google Scholar]
- 22.Sibole SC, Erdemir A. Chondrocyte deformations as a function of tibiofemoral joint loading predicted by a generalized high-throughput pipeline of multi-scale simulations. PLoS One 2012; 7: e37538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Darling EM, Wilusz RE, Bolognesi MP, Zauscher S, Guilak F. Spatial mapping of the biomechanical properties of the pericellular matrix of articular cartilage measured in situ via atomic force microscopy. Biophysical journal 2010; 98: 2848–2856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Korhonen RK, Herzog W. Depth-dependent analysis of the role of collagen fibrils, fixed charges and fluid in the pericellular matrix of articular cartilage on chondrocyte mechanics. Journal of biomechanics 2008; 41: 480–485. [DOI] [PubMed] [Google Scholar]
- 25.McLeod MA, Wilusz RE, Guilak F. Depth-dependent anisotropy of the micromechanical properties of the extracellular and pericellular matrices of articular cartilage evaluated via atomic force microscopy. Journal of biomechanics 2013; 46: 586–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wilusz RE, DeFrate LE, Guilak F. A biomechanical role for perlecan in the pericellular matrix of articular cartilage. Matrix Biology 2012; 31: 320–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tanska P, Mononen ME, Korhonen RK. A multi-scale finite element model for investigation of chondrocyte mechanics in normal and medial meniscectomy human knee joint during walking. Journal of biomechanics 2015; 48: 1397–1406. [DOI] [PubMed] [Google Scholar]
- 28.Chan S, Neu C, Komvopoulos K, Reddi AH. Dependence of nanoscale friction and adhesion properties of articular cartilage on contact load. Journal of biomechanics 2011; 44: 1340–1345. [DOI] [PubMed] [Google Scholar]
- 29.Novak T, Seelbinder B, Twitchell CM, van Donkelaar CC, Voytik Harbin SL, Neu CP. Mechanisms and microenvironment investigation of cellularized high density gradient collagen matrices via densification. Advanced functional materials 2016; 26: 2617–2628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wahlquist JA, DelRio FW, Randolph MA, Aziz AH, Heveran CM, Bryant SJ, et al. Indentation mapping revealed poroelastic, but not viscoelastic, properties spanning native zonal articular cartilage. Acta biomaterialia 2017; 64: 41–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Alonso JL, Goldmann WH. Feeling the forces: atomic force microscopy in cell biology. Life sciences 2003; 72: 2553–2560. [DOI] [PubMed] [Google Scholar]
- 32.Dimitriadis EK, Horkay F, Maresca J, Kachar B, Chadwick RS. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophysical journal 2002; 82: 2798–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wenger MP, Bozec L, Horton MA, Mesquida P. Mechanical properties of collagen fibrils. Biophysical journal 2007; 93: 1255–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sophia Fox AJ, Bedi A, Rodeo SA. The basic science of articular cartilage: structure, composition, and function. Sports health 2009; 1: 461–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nguyen AM, Levenston ME. Comparison of osmotic swelling influences on meniscal fibrocartilage and articular cartilage tissue mechanics in compression and shear. Journal of Orthopaedic Research 2012; 30: 95–102. [DOI] [PubMed] [Google Scholar]
- 36.Smith RL, Carter DR, Schurman DJ. Pressure and shear differentially alter human articular chondrocyte metabolism: a review. Clinical Orthopaedics and Related Research® 2004; 427: S89–S95. [PubMed] [Google Scholar]