An Introduction to Kurtosis Fractional Anisotropy

Neuroradiology and imaging-based diagnostics in general have a dire need for scan techniques with improved microstructural sensitivity for detection of subtle tissue alterations in early disease phases or for diagnostics of diseases that are currently simply radiologically invisible. Diseases in which this need is most outspoken are often neurodegenerative diseases such as Alzheimer's disease, multiple sclerosis, and Parkinson's disease but examples also include (mild, repetitive) trauma, addiction, and stroke. Less frequently reported but important nevertheless is the need for sensitive methods for diagnosis and monitoring of patients exposed to poisonous substances. In the industrialized parts of the world, the leading cause of poisoning is carbon monoxide (CO).¹ In the study by Zhang et al² in the present issue of the American Journal of Neuroradiology (AJNR), brain microstructure in CO-poisoned patients is assessed at 3 time points using diffusional kurtosis imaging (DKI) and is correlated to patient cognitive performance. It concluded that DKI metrics provide important information about the damage to the brain due to CO, and supplement cognitive scores. As a first, the study found kurtosis fractional anisotropy (KFA) to have the best diagnostic efficiency based on a standard area under the curve measure. Because this parameter is likely to be somewhat new to many working in the field of neuroradiology, this commentary aims to recapitulate the basis of KFA and what it might indicate about tissue microstructure.

Diffusion MR Imaging and Diffusional Kurtosis Imaging

Water is abundant in the brain, and the water molecules are thermally driven to move ceaselessly and randomly. The local environment of a water molecule determines its mobility. Therefore, water ensemble properties such as mean diffusivity, diffusion anisotropy, and diffusion distribution shape vary among tissues with different compositions. In neural tissue, diffusion variations are seen among tissue microdomains at the subcellular level,³ the intra- or extracellular space, among cell types,⁴ and therefore also on a coarser scale between gray and white matter tissue.⁵ Noninvasive MR imaging–based measurements of brain-water diffusion, therefore, in principle, contain abundant information about the cellular-level tissue composition. Initially, the diffusion MR imaging (dMRI) signal description was based on a Gaussian (normal) diffusion probability distribution,⁶ forming the basis for the familiar diffusion tensor imaging technique. In biologic tissue, however, the overall diffusion behavior observed from an MR imaging voxel is not Gaussian under clinically relevant measurement conditions. To account for non-Gaussian diffusion, a kurtosis term is added to the DTI signal equation, producing the diffusion DKI framework:⁷

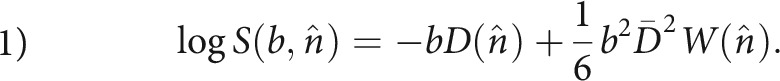Equation 1 describes the behavior of the (log of the) normalized dMRI signal from tissue with diffusion described by a 3 × 3 diffusion tensor D, and kurtosis is described by the 4D tensor W. As written here, the signal is measured along a direction n̂ with diffusion weighting b. The first term on the right-hand side is the DTI signal term, so DTI is fully contained (and actually improved⁸) in DKI. The second term on the right-hand side of Equation 1 is the kurtosis term, with the kurtosis tensor W describing the non-Gaussian properties of the diffusion, which are not contained in D. As written here, D(n̂)is the apparent diffusivity and W(n̂) is the apparent kurtosis, both observed along the diffusion gradient direction n̂. Note that sometimes the apparent kurtosis is referred to as K(n̂), where K(n̂) = W(n̂)D̄²/D(n̂)² (D̄ is mean diffusivity, see below). Simply put, the kurtosis term accounts for the signal deviation from log-linear DTI behavior along the diffusion-encoding direction n̂.

The wealth of information available from DTI and DKI is contained in the diffusion tensor D and the kurtosis tensor W. From D, a number of parameters are available, with typical reported metrics being the apparent diffusion coefficient, ADC = D(n̂); mean diffusivity (D̄ ≡ Tr(D)/3 = (λ₁ + λ₂ + λ₃)/3, where λ₁₋₃ is the diffusion tensor eigenvalues—that is, D(x̂′), D(ŷ′), D(ẑ′) in the tensor eigenframe); radial and axial diffusivities; and fractional anisotropy (FA).⁹ In white matter, the direction with the highest diffusivity (axial diffusivity) largely identifies the main fiber direction.^10–12 The pronounced anisotropy of brain white matter is due to the myelin sheath, the axonal membrane itself, and the cytoskeleton inside the axon,¹³ which collectively cause WM FA to be high (typically >0.6, however see the example below). In DKI, D and W are used together to provide more parameters. These tensors will behave very differently: For example, in a single fiber system, the observed diffusion is high along the fiber direction and low across the fiber direction. In contrast, the kurtosis would be higher across than along the fiber direction, mostly due to restriction effects. This added information improves the capability of dMRI to detect changes in brain and body organ microstructure.^14,15 From DKI, typically reported metrics are analogously the mean kurtosis (MK) and radial and axial kurtosis, and, for very aligned WM, a set of biomarkers from the WM tract integrity framework.¹⁶ More recently, the KFA has been introduced.^17,18 These parameters, their estimation, and varying definitions are reviewed in Hansen and Jespersen.¹⁹

A comprehensive review of DKI in neuroimaging is outside the scope of this commentary, but to illustrate the potential of DKI, we list key neurologic disorders and neuroradiologic areas where DKI has already proved useful: addiction,²⁰ stroke,^21–23 Alzheimer's disease,²⁴ multiple sclerosis,²⁵ Parkinson's disease,^26–29 brain cancer (gliomas),^30,31 and head trauma/concussion.^32–36 While DKI is increasingly used, so far the relatively new KFA has not been given much attention in preclinical and clinical studies. It is, therefore, noteworthy that KFA features prominently in the article of Zhang et al.² Thus, KFA and its interpretation are the main focus of the remainder of this commentary.

dMRI Anisotropy Measures: FA and KFA

The DKI framework produces 2 scalar anisotropy measures: the FA from the diffusion tensor D and the KFA from the kurtosis tensor W. The FA is defined as

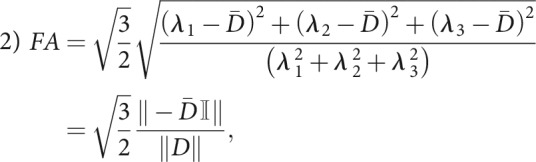where double bars denote the Euclidean tensor norm (the Frobenius norm), 𝕀 is the 3 × 3 identity matrix, and the remaining parameters are defined above. The numeric front factor ensures that that the FA assumes values in the range from 0 (completely isotropic diffusion) to 1 (fully anisotropic, unidirectional diffusion). Although a few alternative definitions of the kurtosis anisotropy have been proposed (notably the one in Poot et al³⁷), the agreed upon definition today is the one introduced in Hansen et al:¹⁸

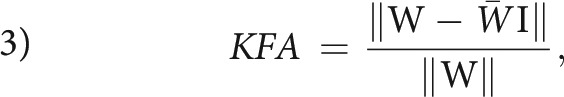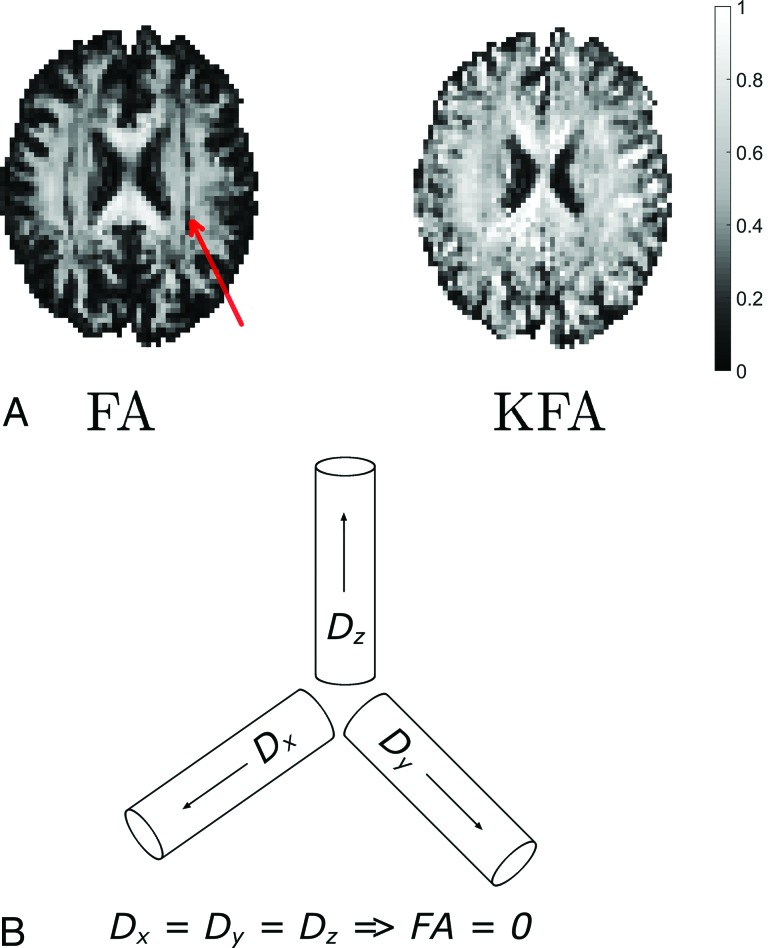
where W is the kurtosis tensor, W̄ is the kurtosis tensor mean,^18,38,39 and I is the fully symmetric rank 4 isotropic tensor. Conveniently, this definition of KFA is analogous to the FA definition in Equation 2, with the only difference being due to tensor dimensions. We note the absence of a numeric front factor in Equation 3; KFA naturally assumes values in the 0–1 range. Interested readers are referred to early explorations of KFA in Hansen and Jespersen¹⁷ and Glenn et al.⁴⁰ In these studies, simulations and experiments were used to investigate the information contained in the KFA. It was found that KFA contrast supplements the FA in important ways. This feature is illustrated in the Figure showing side-by-side maps of FA and KFA in the same image plane position in normal human brain (Fig 1A).

FIGURE.

A, Maps of FA and KFA in the same section position in the normal human brain. The color bar on the right applies to both parameter maps. In the FA map in A, a band of low FA values is seen as a dark band in both hemispheres. The red arrow points to this feature. The same white matter region is seen to have KFA values similar to those of the surrounding white matter. B, The fiber arrangement causing this FA behavior is illustrated in a simplified thought experiment. Figure adapted with permission from Hansen and Jespersen.¹⁷

The red arrow points to a dark band in the FA map inside the WM. This band is seen in both hemispheres (note the symmetry). In each hemisphere, this band comprises voxels with low FA values, though the voxels are located in anatomic WM. Conversely, in the KFA map on the right in Fig 1A, we see that KFA in WM is high and notably retains its high value in the regions where FA fails as a reporter of anisotropy. These WM voxels assume low FA values because they contain a crossing-fiber arrangement in which WM fibers along 3 orthogonal directions weave between each other. This effectively produces the situation illustrated in the schematic in Fig 1B, which shows 3 separate WM fiber bundles that intersect at right angles. In this example, we ignore extra-axonal diffusion. We see that if diffusivities in the 3 fibers are similar (as they are likely to be), the mean diffusivity will be the same as the eigenvalues (ie, the diffusivities along 3 fiber directions D̄ = (λ₁ + λ₂ + λ₃)/3 ≈ λ₁₋₃) causing the FA to vanish because, in this case, each term in the numerator in the middle expression in Equation 2 will be approximately zero. This happens despite the diffusivity in this fiber arrangement being highly anisotropic. Although not particularly complex, the anisotropy in this fiber arrangement cannot be described by the diffusion tensor, resulting in the low FA constituting the dark band in this WM region.

In the interpretation of these metrics, it is crucial to remember that FA and KFA report on different features of the diffusion process. We, therefore, stress that FA summarizes the spatial variation of diffusion rates, whereas KFA summarizes the directional variation in the degree of non-Gaussian diffusion. Loosely speaking, another difference is that the KFA stems from the kurtosis tensor, which is a 4D tensor with much more “room” to capture, in detail, the spatial variation in kurtosis. Collectively, these factors contribute to the demonstrated behavior in which KFA continues to provide contrast in areas where FA does not. Both metrics can be difficult to interpret in strict terms of tissue properties, but on the basis of the simple example above, we can cautiously state that KFA reflects tissue-diffusion complexity. In the example above, we saw that the 2D diffusion tensor cannot resolve anisotropy in voxels with complex fiber composition. However, we also saw that areas with complex fiber arrangements may be distinguished from genuine low-anisotropy regions using FA and KFA in combination: If FA is low and KFA is high, then likely the diffusion is, in fact, anisotropic but the fiber arrangement is too complex to be captured by the diffusion tensor. Thus, the KFA is a good parameter to include in studies in which subtle remodeling is expected in complex tissue regions. While KFA may therefore prove to be a valuable marker of tissue microstructure, we nevertheless stress that no DKI parameter is specifically bound to a particular microscopic tissue component.

Discussion and Future Perspectives

DKI is sometimes omitted from clinical protocols due to longer acquisition and parameter estimation times than a simple DTI protocol. While strategies exist for fast estimation of most DKI parameters,^{18,19,38–44} robust estimation of KFA still requires the full kurtosis tensor W to be determined by fitting on a pixel-by-pixel basis.¹⁷ This requires multishell dMRI data with typically 30 directions and 2–3 nonzero b-values. With modern dMRI techniques, this is possible in clinically feasible scan times.⁴⁵ From such datasets, DKI parameter estimation is possible using any one of the many software packages that exist for dMRI data analysis such as MUSC's DKE software package (https://medicine.musc.edu/departments/centers/cbi/dki/dki-data-processing), which also computes the KFA as defined in Equation 3. As noted above, interpretation of DKI findings in terms of biophysical tissue properties is a difficult problem. In preclinical work, subsequent histology may be used to interpret DKI findings,^15,46,47 and insights gained from such efforts may aid in interpretation of clinical DKI.

In the discussion of the example in the Figure, we noted that KFA somehow reflects the diffusion anisotropy below the voxel level. Other techniques achieve similar sensitivity^48,49 but require nonstandard pulse sequences. Until such techniques reach the clinic in earnest, the KFA may serve as an indicator of the diagnostic potential of such sensitivity.

CONCLUSIONS

Imaging techniques with improved sensitivity to microstructure have utility in many areas of neuroimaging, including diagnosis and monitoring of patients exposed to toxic or poisonous substances. The study by Zhang et al² uses the microstructurally sensitive DKI framework to assess cerebral damage in CO-poisoned subjects. From DKI, the authors obtain measures of mean diffusivity, FA, MK, and the less explored KFA. These measures are then correlated to neuropsychiatric scores. The work presents a timely contribution to 2 avenues of neuroradiology: 1) the exploration of DKI and KFA in clinical practice, and 2) identification of sensitive markers for diagnostics of CO-intoxicated patients. Insights gained from this study may also benefit and inspire many other areas of neuroimaging where the same techniques could be used. With this commentary, we hope that the KFA will have become more familiar to readers of AJNR so that investigators will consider it a parameter of interest in their future work.