Fig. 2.

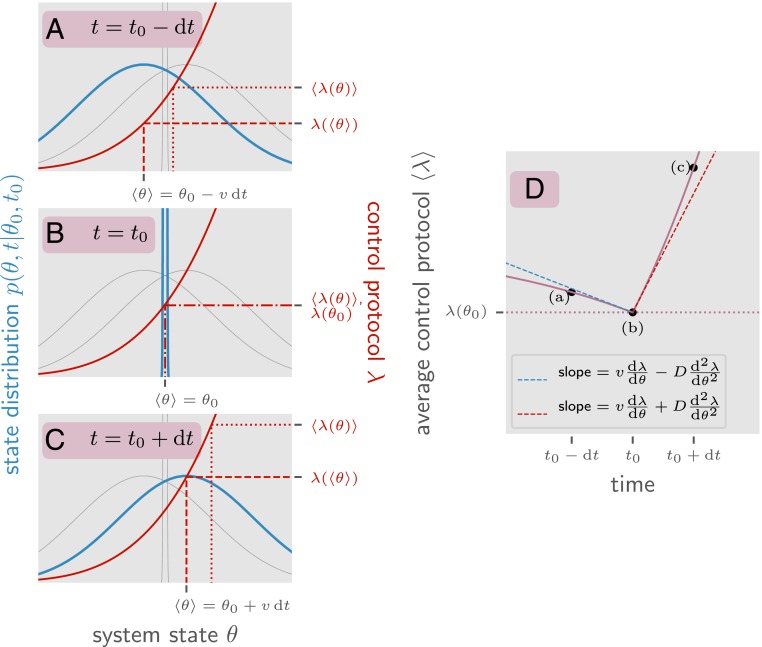
An illustration of why the time derivative of the ensemble value of $\lambda$ is discontinuous. This system state is described by a variable $\theta$ with net drift $v$ and diffusion $D$ (explicitly $\stackrel{\cdot }{\theta }=v+\sqrt{2D}\eta$) and a control function $\lambda \left(\theta \right)$. Here we look at the ensemble $\mathrm{\Lambda }$ of all possible system trajectories $\theta \left(\tau \right)$ such that $\theta \left(t_0\right)={\theta }_0$ for a fixed point $\left(t_0,{\theta }_0\right)$. $\left(A-C\right)$ In blue is the probability of finding the system at a particular value of $\theta$ conditioned on the system being at ${\theta }_0$ at time $t_0$ for three different times: immediately before $t_0\hspace{0.17em}\left(A\right)$, at $t_0\hspace{0.17em}\left(B\right)$, and directly after $t_0\hspace{0.17em}\left(C\right)$. Since the value of $\theta$ at $t_0$ is known, $B$ is a Dirac delta function. $A$ and $C$ are identical Gaussians shifted forward and backward by $v\mathrm{d}t$. In red is the value of the control parameter $\lambda$ as a function of $\theta$. The important quantity is $⟨\lambda \left(\theta \right)⟩$, the value of $\lambda \left(\theta \right)$ at a given time averaged over trajectories in $\mathrm{\Lambda }$. Note that while $⟨\theta ⟩$ increases as a function of time (from $A$ to $C$) and $\lambda \left(\theta \right)$ increases as a function of $\theta$, it is not the case that $⟨\lambda \left(\theta \right)⟩$ increases as a function of time. This is because of diffusion. Between $B$ and $C$, the distribution of $\theta$ diffuses away from ${\theta }_0$. Because $\lambda$ is convex, this causes $⟨\lambda \left(\theta \right)⟩$ to increase. The same argument applies backward in time as well. As we move backward in time from $B$ to $A$ the $\theta$ distribution also diffuses away from ${\theta }_0$, which in turn increases $⟨\lambda \left(\theta \right)⟩$ due to the convexity of $\lambda \left(\theta \right)$. This means that the minimum value of $⟨\lambda \left(\theta \right)⟩$ occurs at the intermediate time $t_0$. This is the origin of the discontinuity shown in $\left(D\right)$. $\left(D\right)$ In purple is a plot of $⟨\lambda \left(\theta \right)⟩$ over time averaged over the same ensemble of trajectories $\mathrm{\Lambda }$. The time derivative has a discontinuity at $t=t_0$ related to ${\mathrm{d}}^2\lambda /\mathrm{d}{\theta }^2$ (the convexity of $\lambda$). The left- and right-sided limits of the time derivative (shown in blue and red) are the derivatives given by the Ito and reverse-Ito conventions for stochastic calculus (40).